Combined Equation of Lines When Their Slopes are Given

Science > Mathematics > Pair of Straight Lines > Combined Equation of Lines When Their Slopes are Given

In this article, we shall study to find a combined or joint equation of pair of lines when the slopes of lines are given.

Algorithm:

• Locate slopes m1 and m2 of the two lines.
• Use y = mx form to find equations of the two lines.
• Write equations of lines in the form u = 0 and  v = 0. Find u.v = 0.
• Simplify the L.H.S. of the joint equation.

Example 01:

• Find the joint equation of a pair of lines through the origin having slopes  1 and 3.
• Solution:

Let l₁ and l₂  be the two lines. Slope of l₁ is 1 and that of l₂  is 3

Therefore the equation of line (l₁) passing through origin and having slope 1 is

y = 1 (x)

∴ x  –  y = 0 ……. (1)

Similarly the equation of line (l₂) passing through origin and having slope 3 is

y = 3 (x)

∴ 3 x – y = 0  …. (2)

From (1) and (2) the required combined equation is

(x – y) (3x – y) = 0

∴ x(3x – y) – y(3x – y) = 0

∴ 3x² – xy – 3xy + y² = 0

∴ 3x² – 4xy + y² = 0

This is the required cobined equation.

Example 02:

• Find the joint equation of a pair of lines through the origin having slopes  4 and -1.

Solution:

Let l₁ and l₂  be the two lines. Slope of l₁ is 4 and that of l₂  is – 1

Therefore the equation of line (l₁) passing through origin and having slope 4 is

 y = 4 (x)

∴   4x – y = 0  ……. (1)

Similarly the equation of line (l₂) passing through origin and having slope -1 is

y = -1 (x)

∴ x + y = 0  …. (2)

From (1) and (2) the required combined equation is

(4x – y) (x + y) = 0

∴ 4x(x + y) – y(x + y) = 0

∴ 4x² + 4xy – xy + y² = 0

∴ 4x² + 3xy + y² = 0

This is the required cobined equation.

Example 03:

• Find the joint equation of a pair of lines through the origin having slopes  2 and – 1/2.
• Solution:

Let l₁ and l₂  be the two lines. Slope of l₁ is 2 and that of l₂  is – 1/2

Therefore the equation of line ( l₁) passing through origin and having slope 2 is

y = 2 (x)

∴ 2x – y = 0 ……. (1)

Similarly the equation of line (l₂) passing through origin and having slope  is

y =  -1/2 (x)

∴ 2y = – x

∴  x + 2y = 0  ………. (2)

From (1) and (2) the required combined equation is

(2x – y) (x + 2y) = 0

∴ 2x(x + 2y) – y(x + 2y) = 0

∴ 2x² + 4xy – xy – 2y² = 0

∴ 2x² + 3xy – 2y² = 0

This is the required cobined equation.

Example 04:

• Find the joint equation of a pair of lines through the origin having slopes 1/3  and -1/2.

Solution:

Let l₁ and l₂  be the two lines. Slope of l₁ is 1/3 and that of l₂  is – 1/2

Therefore the equation of line (l₁) passing through origin and having slope  is

y = 1/3 (x)

∴  3y = x

∴  x – 3y = 0  ……. (1)

Similarly the equation of line (l₂) passing through origin and having slope  is

y =  (x)

∴  2y = -x

∴  x + 2y = 0  ……. (2)

From (1) and (2) the required combined equation is

(x – 3y) (x + 2y) = 0

∴ x(x + 2y) – 3y(x + 2y) = 0

∴ x² + 2xy – 3xy – 6y² = 0

∴ x² – xy = 6y² = 0

This is the required cobined equation.

Example 05:

• Find the joint equation of a pair of lines through the origin having slopes 1 + √3  and 1 – √3.
• Solution:

Let l₁ and l₂  be the two lines. Slope of l₁ is 1 + √3 and that of l₂  is 1 – √3

Therefore the equation of line (l₁) passing through origin and having slope  is

y = (1 + √3)x

∴   (1 + √3)x – y = 0 …. (1)

Similarly, the equation of the line (l₂) passing through the origin and having slope   is

y = ( 1 – √3)x

∴  ( 1 – √3)x – y = 0 …. (2)

From (1) and (2) the required combined equation is

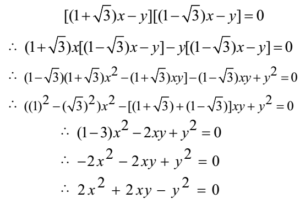
This is the required combined equation.

Science > Mathematics > Pair of Straight Lines > Combined Equation of Lines When Their Slopes are Given