Science > Mathematics > Coordinate Geometry > Locus > Equation of the Locus
In this article, we shall study the concept of locus and to find the equation of the locus.
Example – 46:
A(3, 1) and B(2, -5) are the vertices of a triangle. Find the equation of locus of the third vertex C, if the centroid of the triangle lies on the locus y = 3 + 2x2.
Solution:
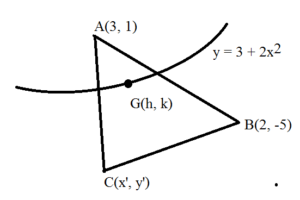
let G(h, k) be the centroid. It lies on the locus y = 3 + 2x2
Hence it should satisfy the equation of the locus
k = 3 + 2h2 ……….. (1)
Let C(x’, y’) be the third vertex of the triangle, whose locus is to be found
By Centroid formula
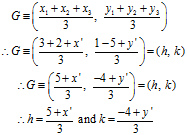
Substituting in equation (1)
(-4 + y’)/3 = 3 + 2((5+x’)/3)2
(-4 + y’)/3 = 3 + 2(25+ 10x’ +x’2)/9
Multiplying both sides by 9
3(-4 + y’) = 27 + 2(25+ 10x’ +2x’2)
-12 + 3y’ = 27 + 50+ 20x’ + 2x’2
27 + 50+ 20x’ + 2x’2 + 12 – 3y’ = 0
2x’2 + 20x’ – 3y’ + 89 = 0
Replacing x’ with x and y’ with y we get
2x2 + 20x – 3y + 89 = 0
Ans: The equation of the required locus is 2x2 + 20x – 3y + 89 = 0
Example – 47:
A(3, -2) and B(-2, 4) are the vertices of a triangle. Find the equation of locus of the third vertex C, if the centroid of the triangle lies on the locus 3x2 – 5y2 = 15.
Solution:
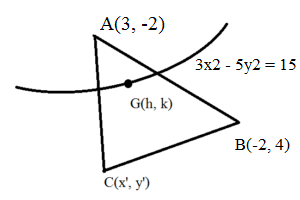
let G(h, k) be the centroid. It lies on the locus 3x2 – 5y2 = 15
Hence it should satisfy the equation of the locus.
3h2 – 5k2 = 15 ……….. (1)
Let C(x’, y’) be the third vertex of the triangle, whose locus is to be found.
By Centroid formula

Substituting in equation (1)
3((1+ x’)/3)2 – 5((2 + y’)/3)2 = 15
3((1+ 2x’ + x’2)/9) – 5((4 + 4y’ + y’2)/9) = 15
Multiplying both sides by 9
3(1+ 2x’ + x’2) – 5(4+ 4y’ + y’2) = 135
3+ 6x’ + 3x’2 – 20 – 20y’ – 5y’2 – 135 = 0
3x’2 – 5y’2 + 6x’ – 20y’ – 152 = 0
Replacing x’ with x and y’ with y we get
3x2 – 5y2 + 6x – 20y – 152 = 0
Ans: The equation of the required locus is 3x2 – 5y2 + 6x – 20y – 152 = 0
Example – 48:
A(2, -5) and B(-7, 6) are the vertices of a triangle. Find the equation of locus of the third vertex C, if the centroid of the triangle lies on the locus 3x – 4y = 11.
Solution:

let G(h, k) be the centroid. It lies on the locus 3x – 4y + 11 = 0
Hence it should satisfy the equation of the locus.
3h – 4k + 11 = 0 ……….. (1)
Let C(x’, y’) be the third vertex of the triangle, whose locus is to be found.
By Centroid formula

Substituting in equation (1)
3((-5+ x’)/3) – 4((1 + y’)/3) + 11 = 0
Multiplying both sides by 3
3(-5+ x’) – 4(1 + y’) + 33 = 0
15+ 3x’ – 4 – 4y’ + 33 = 0
3x’ – 4y’ – 19 + 33 = 0
3x’ – 4y’ + 14 = 0
Replacing x’ with x and y’ with y we get
3x – 4y + 14 = 0
Ans: The equation of the required locus is 3x – 4y + 14 = 0
Example – 49:
A(5, -2) and B(2, 4) are the vertices of a triangle. The third vertex C of triangle lies on the locus y = 1 + x + x2. Find the equation of locus of the centroid of the triangle.
Solution:

let C(h, k) be the centroid. It lies on the locus y = 1 + x + x2
Hence it should satisfy the equation of the locus.
k = 1 + h + h2 ……….. (1)
Let G(x’, y’) be the centroid of the triangle, whose locus is to be found.
By Centroid formula

Substituting in equation (1)
(3y’ – 2) = 1 + (3x’ – 7) + (3x’ – 7)2
3y’ – 2 = 1 + 3x’ – 7 + 9x’2 – 42x’ + 49
1 + 3x’ – 7 + 9x’2 – 42x’ + 49 – 3y’ + 2 = 0
9x’2 – 39x’ – 3y’ + 45 = 0
3x’2 – 13x’ – y’ + 15 = 0
Replacing x’ with x and y’ with y we get
3x2 – 13x – y + 15 = 0
Ans: The equation of the required locus is 3x2 – 13x – y + 15 = 0
Example – 50:
A(3, -2) and B(-2, 4) are the vertices of a triangle. The third vertex C of triangle lies on the locus y = 2 + 3x + x2. Find the equation of locus of the centroid of the triangle.
Solution:

let C(h, k) be the centroid. It lies on the locus y = 2 + 3x + x2
Hence it should satisfy the equation of the locus.
k = 2 + 3h + h2 ……….. (1)
Let G(x’, y’) be the centroid of the triangle, whose locus is to be found.
By Centroid formula

Substituting in equation (1)
3y’ – 7 = 2 + 3(3x’ – 2) + (3x’ – 2)2
3y’ – 7 = 2 + 9x’ – 6 + (9x’2 – 12x’ + 4)
2 + 9x’ – 6 + 9x’2 – 12x’ + 4 – 3y’ + 7 = 0
9x’2 – 3x’ – 3y’ + 7 = 0
Replacing x’ with x and y’ with y we get
9x2 – 3x – 3y + 7 = 0
Ans: The equation of the required locus is 9x2 – 3x – 3y + 7 = 0
Example – 51:
A(1, 4) and B(6, -3) are the vertices of a triangle. The third vertex C of the triangle lies on the locus 5x + 4y = 9. Find the equation of locus of the centroid of the triangle.
Solution:

let C(h, k) be the centroid. It lies on the locus 5x + 4y = 9
Hence it should satisfy the equation of the locus.
5h + 4k = 9 ……….. (1)
Let G(x’, y’) be the centroid of the triangle, whose locus is to be found.
By Centroid formula

Substituting in equation (1)
5(3x’ – 7) + 4(3y’ – 1) = 9
15x’ – 35 + 12y’ – 4 = 9
15x’ + 12y’ -39 – 9 = 0
15x’ + 12y’ – 48 = 0
5x’ + 4y’ – 16 = 0
Replacing x’ with x and y’ with y we get
5x + 4y – 16 = 0
Ans: The equation of the required locus is 5x + 4y – 16 = 0
Example – 52:
A(4, -3) and C(0, 2) are the vertices of a triangle. The third vertex B of the triangle lies on the locus y = 1+ x2. Find the equation of locus of the centroid of the triangle.
Solution:

let B(h, k) be the centroid. It lies on the locus y = 1+ x2
Hence it should satisfy the equation of the locus.
k = 1+ h2 ……….. (1)
Let G(x’, y’) be the centroid of the triangle, whose locus is to be found.
By Centroid formula

Substituting in equation (1)
(3y’ + 1) = 1 +(3x’ – 4)2
3y’ + 1 = 1 +9x’2 – 24x’ + 16
1 +9x’2 – 24x’ + 16 – 3y’ – 1 = 0
9x’2 – 24x’ – 3y’ + 16 = 0
Replacing x’ with x and y’ with y we get
9x2 – 24x – 3y + 16 = 0
Ans: The equation of the required locus is 9x2 – 24x – 3y + 16 = 0