New Equation of Locus After Shifting Origin

Science > Mathematics > Coordinate Geometry > Locus > New Equation of Locus After Shifting Origin

Type – I: To Find New Equation of Locus After Shifting the Origin

Example – 01:

The origin is shifted to the point (1, -4). Find the new equation of locus 2x² – xy + 3y² – 8x + 25 y + 54 = 0 axes remaining parallel.

Solution:

The old equation of locus is 2x² – xy + 3y² – 8x + 25 y + 54 = 0 …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (1, -4)

We have x = X + h = X + 1 and y = Y + k = Y – 4

Substituting these values in equation (1) we have

2(X + 1)² – (X + 1)( Y – 4) + 3( Y – 4)² – 8(X + 1) + 25 ( Y – 4) + 54 = 0

∴  2(X² + 2X + 1) – (XY – 4X + Y – 4) + 3( Y² – 8Y + 16) – 8X -8 + 25 Y – 100 + 54 = 0

∴  2X² + 4X + 2 – XY + 4X – Y + 4 + 3Y² – 24Y + 48 – 8X -8 + 25 Y – 100 + 54 = 0

∴  2X² – XY + 3Y² = 0

Ans: The new equation of locus is 2X² – XY + 3Y² = 0

Example – 02:

The origin is shifted to the point (1, 1). Find the new equation of locus xy – x – y + 1 = 0 axes remaining parallel.

Solution:

The old equation of locus is xy – x – y + 1 = 0 …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (1, 1)

We have x = X + h = X + 1 and y = Y + k = Y + 1

Substituting these values in equation (1) we have

(X + 1)( Y + 1) – (X + 1) – (Y + 1) + 1 = 0

∴  XY + X + Y + 1 – X – 1 – Y – 1 + 1 = 0

∴  XY  = 0

Ans: The new equation of locus is XY  = 0

Example – 03:

The origin is shifted to the point (1, 1). Find the new equation of locus x² – y² – 2x + 2y = 0 axes remaining parallel.

Solution:

The old equation of locus is x² – y² – 2x + 2y = 0 …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (1, 1)

We have x = X + h = X + 1 and y = Y + k = Y + 1

Substituting these values in equation (1) we have

(X + 1)² – (Y + 1)² – 2(X + 1) + 2(Y + 1) = 0

∴  (X² + 2X + 1) – ( Y² + 2Y + 1) – 2X -2 + 2Y  + 2 = 0

∴  X² + 2X + 1 – Y² – 2Y  – 1 – 2X -2 + 2Y  + 2 = 0

∴  X² – Y² = 0

Ans: The new equation of locus is X² – Y² = 0

Example – 04:

The origin is shifted to the point (1, 1). Find the new equation of locus x² + y² – 4x + 6y +3 = 0 axes remaining parallel.

Solution:

The old equation of locus is x² + y² – 4x + 6y +3 = 0 …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (1, 1)

We have x = X + h = X + 1 and y = Y + k = Y + 1

Substituting these values in equation (1) we have

(X + 1)² + (Y + 1)² – 4(X + 1) + 6(Y + 1) + 3 = 0

∴  (X² + 2X + 1) + (Y² + 2Y + 1) – 4X – 4 + 6Y + 6 + 3 = 0

∴  X² + 2X + 1 + Y² + 2Y + 1 – 4X – 4 + 6Y + 6 + 3 = 0

∴  X² + Y² – 2X + 8Y + 7 = 0

Ans: The new equation of locus is X² + Y² – 2X + 8Y + 7 = 0

Example – 05:

The origin is shifted to the point (2, -1). Find the new equation of locus 2x² + 3xy – 9y² – 5x – 24y – 7 = 0 axes remaining parallel.

Solution:

The old equation of locus is 2x² + 3xy – 9y² – 5x – 24y – 7 = 0 …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (2, -1)

We have x = X + h = X + 2 and y = Y + k = Y – 1

Substituting these values in equation (1) we have

2(X + 2)² + 3(X + 2) (Y – 1) – 9(Y – 1)² – 5(X + 2) – 24(Y – 1) – 7 = 0

∴  2(X² + 4X + 4) + 3(XY – X + 2Y – 2) – 9(Y² – 2Y + 1) – 5X – 10 – 24Y + 24 – 7 = 0

∴  2X² + 8X + 8 + 3XY – 3X + 6Y – 6 – 9Y² + 18Y  – 9 – 5X – 10 – 24Y + 24 – 7 = 0

∴  2X² + 3XY – 9Y² = 0

Ans: The new equation of locus is 2X² + 3XY – 9Y² = 0

Example – 06:

The origin is shifted to the point (a – c, b). Find the new equation of locus (x – a)² + (y – b)² = r² axes remaining parallel.

Solution:

The old equation of locus is (x – a)² + (y – b)² = r² …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (a – c, b)

We have x = X + h = X + a – c and y = Y + k = Y + b

Substituting these values in equation (1) we have

(X + a – c – a)² + (Y + b – b)² = r²

∴  (X – c)² + (Y)² = r²

∴  (X – c)² + (Y)² = r²

∴  X² – 2cX + c² + Y² = r²

∴  X² + Y² – 2cX + c² – r² = 0

Ans: The new equation of locus is X² + Y² – 2cX + c² – r² = 0

Example – 07:

The origin is shifted to the point (1/2, -3/2). Find the new equation of locus (2x – 1)² + (y + 3/2)² = 4 axes remaining parallel.

Solution:

The old equation of locus is (2x – 1)² + (y + 3/2)² = 4  …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (1/2, -3/2)

We have x = X + h = X + 1/2 and y = Y + k = Y – 3/2

Substituting these values in equation (1) we have

(2(X + 1/2) – 1)² + ((Y – 3/2) + 3/2)² = 4

∴  (2X + 1 – 1)² + (Y – 3/2 + 3/2)² = 4

∴  (2X)² + (Y)² = 4

∴  4X² + Y² = 4

Ans: The new equation of locus is 4X² + Y² = 4

Example – 08:

The origin is shifted to the point (-1, 2). Find the new equation of locus 4x² + y² + 6x – 4y + 5 = 0 axes remaining parallel.

Solution:

The old equation of locus is 4x² + y² + 8x – 4y + 4 = 0  …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (2, -1)

We have x = X + h = X – 1 and y = Y + k = Y + 2

Substituting these values in equation (1) we have

4(X – 1)² + (Y + 2)² + 8(X – 1) – 4(Y + 2) + 4 = 0

∴  4(X² – 2X +  1) + (Y² + 4Y + 4) + 8X – 8 – 4Y – 8 + 4 = 0

∴  4X² – 8X +  4 + Y² + 4Y + 4 + 8X – 8 – 4Y – 8 + 4 = 0

∴  4X² + Y² – 4 = 0

∴  4X² + Y² = 4

Ans: The new equation of locus is 4X² + Y² = 4

Example – 09:

Obtain the new equation of locus (a – b)(x² + y²) – 2abx = 0. If the origin is shifted to the point (ab/(a-b), 0) axes remaining parallel.

Solution:

The old equation of locus is (a – b)(x² + y²) – 2abx = 0   …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (2, -1)

We have x = X + h = X + ab/(a-b) and y = Y + k = Y + 0 = Y

Substituting these values in equation (1) we have

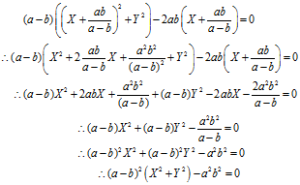
Ans: The new equation of locus is (a – b)²(X² + Y²) – a²b² = 0

Type – II: To Find Old Equation of Locus After Shifting the Origin

Example – 10:

The origin is shifted to the point (5, -3). The equation of locus in new system is Y² = 6X. Find the equation of locus in the old system

Solution:

The new equation of locus is Y² = 6X  …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (5, -3)

We have X = x – h = x – 5 and Y = y – k = y + 3

Substituting these values in equation (1) we have

(y + 3)² = 6(x – 5)

∴  y² + 6y + 9 = 6x – 30

∴  y² – 6x + 6y + 39 = 0

Ans: The equation of locus in old system is y² – 6x + 6y + 39 = 0

Example – 11:

The origin is shifted to the point (-1, 2). The equation of locus in new system is X² + 5XY + 3Y² = 0. Find the equation of locus in the old system

Solution:

The new equation of locus is X² + 5XY + 3Y² = 0 …………. (1)

Let (x, y) be the old coordinates and (X, Y) be the new coordinates after shifting the origin to (h, k) ≡ (-1, 2)

We have X = x – h = x + 1 and Y = y – k = y – 2

Substituting these values in equation (1) we have

(x + 1)² + 5(x + 1)(y -2) + 3(y -2)² = 0

∴  (x² + 2x + 1) + 5(xy – 2x + y – 2) + 3(y² – 4y + 4) = 0

∴  x² + 2x + 1 + 5xy – 10x + 5y – 10 + 3y² – 12y + 12 = 0

∴  x² + 5xy + 3y² – 8x – 7y + 3 = 0

Ans: The equation of locus in old system is x² + 5xy + 3y² – 8x – 7y + 3 = 0

Science > Mathematics > Coordinate Geometry > Locus > New Equation of Locus After Shifting Origin