Science > Mathematics > Coordinate Geometry > Locus > Equation of Locus
In this article we shall study the concept of locus and to find the equation of locus of a point using distance formula.
Example – 31:
Find the equation of the locus of a point such that its distance from (5, 0) is equal to a distance from the y-axis.
Solution:
Let P(x. y) be the point on the locus, A(5. 0) be the point
Distance of point from y-axis = x
Given: AP = x
∴ AP² = x²
∴ [(x – 5 )² + (y – 0)² ] = x²
∴ x ² – 10x + 25 + y ² = x²∴ – 10x + 25 + y ² = 0
∴ y ² – 10x + 25 =0
Hence required equation of the locus is y ² – 10x + 25 = 0
Example – 32:
Find the equation of the locus of a point which is equidistant from (1, 3) and the x-axis.
Solution:
Let P(x. y) be the point on the locus, A(1, 3) be the point
Distance of point from x-axis = y
Given: AP = y
∴ AP² = y²
∴ [(x – 1 )² + (y – 3)² ] = y²
∴ x ² – 2x + 1 + y ² – 6y + 9 = y²
∴ x ² – 2x – 6y + 10 = 0
Hence required equation of the locus is x ² – 2x – 6y + 10 = 0
Example – 33:
Find the equation of locus of a point such that, the sum of the square of its distances from the points (2, 5) and (3, -1) is 40.
Solution:
Let P(x. y) be the point on the locus, Given A(2, 5) and B(3, -1) be the given points
Given PA² + PB² = 40
∴ [(x – 2 )² + (y – 5)² ] + [(x – 3)² + (y + 1)²] = 40
∴ x² – 4x + 4 + y² – 10y + 25 + x² – 6x + 9 + y² + 2y + 1 = 40
∴ 2x² + 2y² – 10x – 8y – 1 = 0
Hence required equation of the locus is 2x² + 2y² – 10x – 8y – 1 = 0
Example – 34:
Find the equation of locus of a point such that, its distance from (a, 0) is m times its distance from (0, a)
Solution:
Let P(x. y) be the point on the locus, Given A(a, o) and B(0, a) be the given points
Given PA = m. PB
∴ PA² = m². PB²
∴ [(x – a )² + (y – 0)² ] = m²[(x – 0)² + (y – a)²]
∴ x² – 2ax + a² + y² = m²( x² + y² – 2ay + a²)
∴ x² – 2ax + a² + y² = m²x² + m²y² – 2am²y + a²m²
∴ x² – 2ax + a² + y² – m²x² – m²y² + 2am²y – a²m² = 0
∴ (1 – m²) x² + ( 1 – m²) y² – 2ax + 2am²y + (1 – m²) a² = 0
∴ (1 – m²)( x² + y² ) – 2ax + 2am²y + a²(1 – m²) = 0
Hence required equation of the locus is (1 – m²)( x² + y² ) – 2ax + 2am²y + a²(1 – m²) = 0
Example – 35:
The point S is (3, 0) and abscissa of point M is -3. A variable point P is such that ordinates of P and M are equal. Find the equation of locus of point P such that SP = PM.
Solution:
Let P(x. y) be the point on the locus, Given S(3,0)
The abscissa of point M is -3 and its ordinate is same as P i.e. y. Hence M(-3, y) is the point
Given SP = PM
∴ SP² = PM²
∴ [(x – 3 )² + (y – 0)² ] = [(x + 3)² + (y – y)²]
∴ x² – 6x + 9 + y² = x² + 6x + 9 + 0
∴ x² – 6x + 9 + y² – x² – 6x – 9 = 0
∴ – 12x + y² = 0
∴ y² – 12x = 0
Hence required equation of the locus is y² – 12x = 0
Example – 36:
Find the equation of locus of a point which moves such that the ratio of its distances from (2, 0) and (1, 3) is 5:4.
Solution:
Let P(x. y) be the point on the locus and A(2,0) and B(1, 3) be the points
Given PA/ PB = 5/4
∴ 4 PA = 5 PB
∴ 16 PA² = 25 PB²
∴ 16 [(x – 2)² + (y – 0)² ] = 25[(x – 1)² + (y – 3)²]
∴ 16(x² – 4x + 4 + y² ) = 25(x² – 2x + 1 + y² – 6y + 9)
∴ 16x² – 64x + 64 + 16y² = 25x² – 50x + 25 + 25 y² – 150y + 225
∴ 25x² – 50x + 25 + 25 y² – 150y + 225 – 16x² + 64x – 64 – 16y² = 0
∴ 9x² + 9 y² + 14x – 150y – 186 = 0
Hence required equation of the locus is 9x² + 9 y² + 14x – 150y – 186 = 0
Example – 37:
Find the equation of locus of a point such that the sum of its distances from co-ordinate axes is thrice its distance from the origin.
Solution:
Let P(x. y) be the point on the locus and O(0,0) be the origin
Distance of point from y-axis = x
Distance of point from x-axis = y
Given x + y = 3OP
(x + y)² = 9OP²
∴ x² + 2xy + y²= 9[(x – 0)² + (y – 0)²]
∴ x² + 2xy + y² = 9x ² + 9y²
∴ 9x ² + 9y² – x² – 2xy – y² = 0
∴ 8x ² + 8y² – 2xy = 0
∴ 4x ² + 4y² – xy = 0
Hence required equation of the locus is 4x ² – xy + 4y²= 0
Example – 38:
A(4, 0) and B(-4, 0) are two given points. A variable point P such that PA + PB = 10, show that the equation of locus of point P is
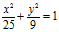
Solution:
Let P(x. y) be the point on the locus and A(4, 0) and B(-4, 0) be the points
Given PA + PB = 10
∴ √(x – 4)² + ( y – 0)² + √(x + 4)² + ( y – 0)² =10
∴ √x² – 8x + 16 + y ² + √x² + 8x + 16 + y² =10
∴ √x² – 8x + 16 + y ² = 10 – √x² + 8x + 16 + y²
Squaring both sides
∴ x² – 8x + 16 + y ² = 100 – 20 √x² + 8x + 16 + y² + x² + 8x + 16 + y ²
∴ – 8x = 100 – 20 √x² + 8x + 16 + y² + 8x
∴ 20 √x² + 8x + 16 + y² =100 + 16x
Squaring both sides
400(x² + 8x + 16 + y ²) = 10000 + 3200x + 256x²
∴ 400x² + 3200x + 6400 + 400y ² = 10000 + 3200x + 256x²
∴ 400x² – 256x² + 400y ² = 10000 – 6400
∴ 144x² + 400y ² = 3600
Dividing both sides by 3600
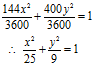
Proved as required
Example – 39:
A(5, 0) and B(-5, 0) are two given points. A variable point P such that PA – PB = 6, show that the equation of locus of point P is
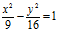
Solution:
Let P(x. y) be the point on the locus and A(5, 0) and B(-5, 0) be the points
Given PA – PB = 6
∴ √(x – 5)² + ( y – 0)² – √(x + 5)² + ( y – 0)² =6
∴ √x² – 10x + 25 + y ² – √x² + 10x + 25 + y² = 6
∴ √x² – 10x + 25 + y ² = 6 + √x² + 10x + 25 + y²
Squaring both sides
∴ x² – 10x + 25 + y ² = 36 + 12 √x² + 10x + 25 + y² + x² + 10x + 25 + y ²
∴ – 10x = 36 + 12 √x² + 10x + 25 + y² + 10x
∴ – 12 √x² + 10x + 25 + y² = 36 + 20x
Squaring both sides
144(x² + 10x + 25 + y ²) = 1296 + 1440x + 400x²
∴ 144x² + 1440x + 3600 + 144 y ² = 1296 + 1440x + 400x²
∴ 400x² – 144x² – 144 y ² = 3600 – 1296
∴ 256x² – 144 y ² = 2304
Dividing both sides by 2304

Proved as required
Example – 40:
A(-3, 0) and B(3, 0) are two given points. A variable point P such that AP – PB = 10, show that the equation of locus of point P is

Solution:
Let P(x. y) be the point on the locus and A(-3, 0) and B(3, 0) be the points
Given AP – PB = 10
∴ √(x + 3)² + ( y – 0)² – √(x – 3)² + ( y – 0)² =10
∴ √x² + 6x + 9 + y ² – √x² – 6x + 9 + y² =10
∴ √x² + 6x + 9 + y ² = 10 – √x² – 6x + 9 + y²
Squaring both sides
∴ x² + 6x + 9 + y ² = 100 – 20 √x² – 6x + 9 + y² + x² – 6x + 9 + y ²
∴ 6x = 100 – 20 √x² – 6x + 9 + y² – 6x
∴ 20 √x² – 6x + 9 + y² =100 – 12x
Squaring both sides
400(x² – 6x + 9 + y ²) = 10000 – 2400x + 144x²
∴ 400x² – 2400x + 3600 + 400y ² = 10000 – 2400x + 144x²
∴ 400x² – 144x² + 400y ² = 10000 – 3600
∴ 256x² + 400y ² = 6400
Dividing both sides by 6400

Proved as required
Example – 41:
A(2, 0) and B(-2, 0) are two given points. A variable point P such that the sum of its distances from given points is 6. Find the equation of the locus of point P.
Solution:
Let P(x. y) be the point on the locus and A(2, 0) and B(-2, 0) be the points
Given PA + PB = 10
∴ √(x – 2)² + ( y – 0)² + √(x + 2)² + ( y – 0)² = 6
∴ √x² – 4x + 4 + y ² + √x² + 4x + 4 + y² = 6
∴ √x² – 4x + 4 + y ² = 6 – √x² + 4x + 4 + y²
Squaring both sides
∴ x² – 4x + 4 + y ² = 36 – 12 √x² + 4x + 4 + y² + x² + 4x + 4 + y ²
∴ – 4x = 36 – 12 √x² + 4x + 4 + y² + 4x
∴ 12 √x² + 4x + 4 + y² =36 + 8x
Squaring both sides
144(x² + 4x + 4 + y ²) = 1296 + 576x + 64x²
∴ 144x² + 576x + 576 + 144y ² = 1296 + 576x + 64x²
∴ 144x² + 144y ² – 64x² = 1296 – 576
∴ 80x² + 144y ²= 720
Dividing both sides by 720

This is the required equation of the locus.
Example – 42:
A(c, 0) and B(-c, 0) are two given points. A variable point P such that the sum of its distances from the given point is 2a. Find the equation of locus if b² = a² – c².
Solution:
Let P(x. y) be the point on the locus and A(c, 0) and B(-c, 0) be the points
Given AP – PB = 10
∴ √(x – c)² + ( y – 0)² – √(x + c)² + ( y – 0)² = 2a
∴ √x² – 2cx + c² + y ² – √x²+ 2cx + c² + y² = 2a
∴ √x² – 2cx + c² + y ² = 2a – √x² + 2cx + c² + y²
Squaring both sides
∴ x² – 2cx + c ² + y ² = 4a ² – 4a √x² + 2cx + c² + y² + x² + 2cx + c² + y ²
∴ – 2cx = 2a – 4a √x² + 2cx + c² + y² + 2cx
∴ 4a √x² + 2cx + c² + y² = 4a ² + 4cx
Squaring both sides
16a²(x² + 2cx + c² + y²) = 16a4 + 32a²cx + 16c²x²
∴ 16a²x² + 32a²cx + 16a²c² + 16a²y² = 16a4 + 32a²cx + 16c²x²
∴ 16a²x² – 16c²x² + 16a²y² = 16a4 – 16a²c²
∴ 16(a² – c²)x² + 16a²y² = 16a² ( a² – c²)
Given b² = a² – c²
∴ 16b²x² + 16a²y² = 16a² b²
∴ b²x² + a²y² = a² b²
Dividing both sides by a² b²

This is the equation of locus.
Example – 43 :
Find the equation of locus of a point P so that the segment joining the points (3, 2) and (-5, 1) subtends a right angle at the point P.
Solution:
Method – I (Using Pythagoras Theorem):
Let P(x. y) be the point on the locus, A(3, 2) and B(-5, 1) be the points.
Seg AB subtends right angle at point P, hence ΔPAB is right-angled triangle
Seg AB is the hypotenuse
PA² + PB² = AB²
∴ (x – 3)² + (y – 2)² + (x + 5)² + (y – 1)² = (3 + 5)² + (2 – 1)²
∴ x² – 6x + 9 + y² – 4y + 4 + x² + 10x + 25 + y² – 2y + 1 = 64 + 1
∴ 2 x² + 2y² + 4x – 6y + 39 – 65 = 0
∴ 2 x² + 2y² + 4x – 6y – 26 = 0
∴ x² + y² + 2x – 3y – 13 = 0
Hence required equation of the locus is x² + y² + 2x – 3y – 13 = 0
Method – II (Using Slopes):
Let P(x. y) be the point on the locus, A(3, 2) and B(-5, 1) be the points.
Seg AB subtends right angle at point P
Slope of AP × Slope of BP = -1

∴ y² – y – 2y + 2 = -(x² +5x – 3x -15)
∴ y² – 3y + 2 = – (x² + 2x -15)
∴ y² – 3y + 2 = – x² – 2x +15
∴ y² – 3y + 2 + x² + 2x – 15 = 0
∴ x² + y² + 2x – 3y – 13 = 0
Hence required equation of the locus is x² + y² + 2x – 3y – 13 = 0
Example – 44 :
A(2, 0) and B(-2, 0) are two points. Find the equation of locus of point P, such that ∠ APB is a right angle.
Solution:
Method – I (Using Pythagoras Theorem):
Let P(x. y) be the point on the locus, A(2, 0) and B(-2, 0) be the points.
∠ APB is a right angle, hence ΔPAB is right-angled triangle
Seg AB is the hypotenuse
PA² + PB² = AB²
∴ (x – 2)² + (y – 0)² + (x + 2)² + (y – 0)² = (2 + 2)² + (0 – 0)²
∴ x² – 4x + 4 + y² + x² + 4x + 4 + y² = 16
∴ 2 x² + 2y² = 8
∴ x² + y² = 4
Hence required equation of the locus is x² + y² = 4
Method – II (Using Slopes):
Let P(x. y) be the point on the locus, A(2, 0) and B(-2, 0) be the points.
Seg AB subtends right angle at point P
Slope of AP × Slope of BP = -1

∴ y² = -(x² – 4)
∴ y² = – x² + 4
∴ x² + y² = 4
Hence required equation of the locus is x² + y² = 4
Example – 45 :
A(5, -3) and B(-1, -5) are two points. Find the equation of locus of point P, such that seg AB subtends a right angle at point P.
Solution:
Let P(x. y) be the point on the locus, A(5, -3) and B(-1, -5) be the points.
The seg AB subtends right angle at point P, hence ΔPAB is right-angled triangle
Seg AB is the hypotenuse
PA² + PB² = AB²
∴ (x – 5)² + (y + 3)² + (x + 1)² + (y + 5)² = (5 + 1)² + (-3 + 5)²
∴ x² – 10x + 25 + y² + 6y + 9 + x² + 2x + 1 + y² + 10y + 25 = 36 + 4
∴ 2x² + 2y² – 8x + 16 y + 60 = 40
∴ 2x² + 2y² – 8x + 16 y + 20 = 0
∴ x² + y² – 4x + 8 y + 10 = 0
Hence required equation of the locus is x² + y² – 4x + 8 y + 10 = 0