Science > Mathematics > Coordinate Geometry > Straight Lines > Slope Problems Related With Triangles
In this article, we shall study to find slopes of altitude, median, and perpendicular bisectors of sides of triangle and also the mrthod to prove that given triagle is a right angled triangle using slopes of its sides.
Example – 01:
A(2, 3), B(-2, 1) and C(4, -3) are the vertices of ΔABC. Find the slope of (i) side AB (ii) altitude through A (iii) median through A and (iv) perpendicular bisector of AB.
Solution:
Slope of side AB:
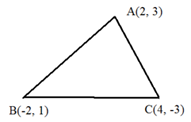
Slope of side AB = (1 – 3)/(-2 – 2) = (-2)/(-4) = 1/2
Slope of Altitude Through A:
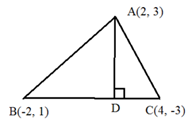
Slope of BC = (-3 -1)/(4 + 2) = (-4)/(6) = – 2/3
Now AD ⊥ side BC
∴ Slope of AD = 3/2
Median Through A:
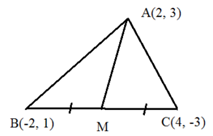
M is midpoint of side BC, By midpoint formula
M ≡ ((-2 + 4)/2, (1 -3)/2) = M(2/2, -2/2) = M(1, -1)
End points of median are A(2, 3) and M (1, -1)
Slope of median through A = (-1 – 3)/(1 – 2) = (-4)/(-1) = 4
Perpenicular bisector of AB:

Slope of side AB = (1 – 3)/(-2 – 2) = (-2)/(-4) = 1/2
line l is perpendicular bisector of side AB
line l ⊥ side AB
Slope of line l = – 2
Example – 02:
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5), and (–1, –1) are the vertices of a right-angled triangle.
Solution:
Let A(4, 4), B(3, 5), and C(-1, -1) be the given points
Slope of AB = (5 – 4)/(3 – 4) = (1)/(-1) = – 1 ………….. (1)
Slope of BC = (-1 – 5)/(-1 – 3) = (-6)/(-4) = 3/2 ………….. (2)
Slope of AC = (-1 – 4)/(-1 – 4) = (-5)/(-5) = 1 ………….. (3)
From equations (1) and (3) we have
Slope of AB x Slope of AC = (-1) x (1) = -1
Thus AB ⊥ AC
Hence ΔABC is right angled at A
∴ The points (4, 4), (3, 5), and (–1, –1) are the vertices of a right-angled triangle.
Example – 03:
Without using the Pythagoras theorem, show that the points (7, 10), (-2, 5) and (3, –4) are the vertices of a right-angled triangle.
Solution:
Let A(7, 10), B(-2, 5), and C(3, -4) be the given points
Slope of AB = (5 – 10)/(-2 – 7) = (-5)/(-9) = 5/9 ………….. (1)
Slope of BC = (-4 – 5)/(3 + 2) = (-9)/(5) = – 9/5 ………….. (2)
Slope of AC = (-4 – 10)/(3 – 7) = (-14)/(-4) = 7/2 ………….. (3)
From equations (1) and (2) we have
Slope of AB x Slope of BC = (5/9) x (- 9/5) = -1
Thus AB ⊥ BC
Hence ΔABC is right angled at B
∴ The points (7, 10), (-2, 5), and (3, -4) are the vertices of a right-angled triangle.
Example – 04:
Show that the points (6, 1), (-1, 8), and (3, -2) form a right angled triangle using slope method.
Solution:
Let A(6, 1), B(-1, 8), and C(3, -2) be the given points
Slope of AB = (8 – 1)/(-1 – 6) = 7/(-7) = – 1 ………….. (1)
Slope of BC = (-2 – 8)/(3 + 1) = – 10/4 = – 5/2 ………….. (2)
Slope of AC = (- 2 – 1)/(3 – 6) = (-3)/(-3) = 1 ………….. (3)
From equations (1) and (3) we have
Slope of AB x Slope of AC = (-1) x (1) = -1
Thus AB ⊥ AC
Hence ΔABC is right angled at A
∴ The points (6, 1), (-1, 8), and (3, -2) form a right angled triangle.
Example – 05:
Show that the points (-1, -4), (4, 6), and (-4, 10) form a right angled triangle using slope method.
Solution:
Let A(-1, -4), B(4, 6), and C(-4, 10) be the given points
Slope of AB = (6 + 4)/(4 + 1) = 10/5 = 2 ………….. (1)
Slope of BC = (10 – 6)/(-4 – 4) = 4/(-8) = – 1/2 ………….. (2)
Slope of AC = (10 + 4)/(- 4 + 1) = (14)/(-3) = – 14/3 ………….. (3)
From equations (1) and (2) we have
Slope of AB x Slope of BC = (2) x (- 1/2) = -1
Thus AB ⊥ BC
Hence ΔABC is right angled at B
∴ The points (-1, -4), (4, 6), and (-4, 10) form a right angled triangle.
Example – 06:
Using the concept of slopes prove that the points (1, 3), (3, -1) and (-5, -5) are the vertices of a right angled triangle.
Solution:
Let A(1, 3), B(3, -1) and C(-5, -5) be the given points
Slope of AB = (-1 – 3)/(3 – 1) = -4/2 = – 2 ………….. (1)
Slope of BC = (-5 + 1)/(-5 – 3) = – 4/(-8) = 1/2 ………….. (2)
Slope of AC = (-5 – 3)/(- 5 – 1) = (-8)/(-6) = 4/3 ………….. (3)
From equations (1) and (2) we have
Slope of AB x Slope of BC = (2) x (- 1/2) = -1
Thus AB ⊥ BC
Hence ΔABC is right angled triangle right angled at B
∴ The points (1, 3), (3, -1) and (-5, -5) are the vertices of a right-angled triangle.