Separate Equations of Lines (Auxiliary Equation Method)

Science > Mathematics > Pair of Straight Lines > Separate Equations of Lines (Auxillary Equation Method)

In this article, we shall study to find separate equations of lines from a combined or joint equation of pair of lines by auxiliary equation method.

Algorithm:

1. Check if lines exist. use the same method used in the case to find the nature of lines. Proceed further if lines exist.
2. Divide both sides of the equation by x².
3. Simplify the equation and substitute y/x = m in it.
4. Find two roots m₁ and m₂ of quadratic equation in m
5. Find separate equations of lines by y = m₁ x and y = m₂x
6. Note that this method is applicable to any problem.

Example 01:

• Obtain the separate equations of the lines represented by  11x² + 8xy + y² = 0
• Solution:

The given joint equation is  11x² + 8xy + y² = 0

Dividing both sides of the equation by x²

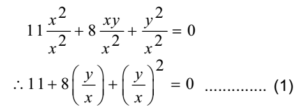
The equation of a line passing through the origin is of the form y = mx

Substituting y/x = m in equation (1) we get

11 + 8m + m² = 0

m² + 8m + 11 = 0

This is a quadratic equation in m and has two roots say m₁ and m₂

which gives slopes of the two lines represented by the joint equation.

a = 1, b = 8, c = 11

The roots are given by

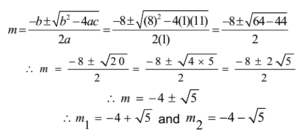
The equation of the first line is

y = m₁x

∴  y = (-4 + √5) x

∴  y = – (4 – √5) x

 ∴  (4 – √5) x  + y = 0

The equation of the second line is

y = m₂x  i.e.  i.e.

∴  y = (-4 – √5) x

∴  y = – (4 + √5) x

 ∴  (4 + √5) x  + y = 0

Ans: The separate equations of the lines are (4 – √5) x  + y = 0 and (4 + √5) x  + y = 0

Example 02:

• Obtain separate equations of lines represented by joint equation x² – 4xy + y² = 0.
• Solution:

The given joint equation is  x² – 4xy + y² = 0

Dividing both sides of the equation by x²

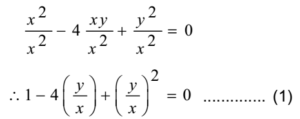
The equation of a line passing through the origin is of the form y = mx

Substituting y/x = m in the equation (1) we get

1 – 4m + m² = 0

∴  m² – 4m + 1= 0

This is a quadratic equation in m and has two roots say m₁ and m₁

which gives slopes of the two lines represented by the joint equation.

a = 1, b = -4, c = 1

The roots are given by

The equation of the first line is

y = m₁x

∴  y = (2 + √3) x

 ∴  (2 + √3) x  – y = 0

The equation of the second line is

y = m₂x

∴  y = (2 – √3) x

 ∴  (2 – √3) x  – y = 0

Ans: The separate equations of the lines are  (2 + √3) x  – y = 0 and (2 – √3) x  – y = 0

Example 03:

• Obtain separate equations of lines represented by joint equation 22x² – 10xy + y² = 0.

Solution:

The given joint equation is 22x² – 10xy + y² = 0.

Dividing both sides of the equation by x²

The equation of a line passing through the origin is of the form y = mx

Substituting y/x = m in the equation (1) we get

22 – 10m + m² = 0

∴  m² – 10m + 22= 0

This is a quadratic equation in m and has two roots say m₁ and m₁

which gives slopes of the two lines represented by the joint equation.

a = 1, b = – 10, c = 22

The roots are given by

The equation of the first line is

y = m₁x

∴  y = (5 + √3) x

 ∴  (5 + √3) x  – y = 0

The equation of the second line is

y = m₂x

∴  y = (5 – √3) x

 ∴  (5 – √3) x  – y = 0

Ans: The separate equations of the lines are  (5 + √3) x  – y = 0 and (5 – √3) x  – y = 0

Example 04:

• Obtain separate equations of lines represented by joint equation x² + 2xy – y² = 0.
• Solution:

The given joint equation is x² + 2xy – y² = 0

Dividing both sides of the equation by x²

The equation of a line passing through the origin is of the form y = mx

Substituting y/x = m in the equation (1) we get

1 + 2m – m² = 0

∴  m² – 2m  – 1= 0

This is a quadratic equation in m and has two roots say m₁ and m₁

which gives slopes of the two lines represented by the joint equation.

a = 1, b = – 2, c = -1

The roots are given by

The equation of the first line is

y = m₁x

∴  y = (1 + √2) x

 ∴  (1 + √2) x  – y = 0

The equation of the second line is

y = m₂x

∴  y = (1 – √2) x

 ∴  (1 – √2) x  – y = 0

Ans: The separate equations of the lines are  (1 + √2) x  – y = 0 and (1 – √2) x  – y = 0

Example 05:

• Obtain separate equations of lines represented by joint equation 2x² + 2xy – y² = 0.

Solution:

The given joint equation is  2x² + 2xy – y² = 0

Dividing both sides of the equation by x²

The equation of a line passing through the origin is of the form y = mx

Substituting y/x = m in the equation (1) we get

2 + 2m – m² = 0

∴  m² – 2m – 2= 0

This is a quadratic equation in m and has two roots say m₁ and m₁

which gives slopes of the two lines represented by the joint equation.

a = 1, b = – 2, c = -2

The roots are given by

The equation of the first line is

y = m₁x

∴  y = (1 + √3) x

 ∴  (1 + √3) x  – y = 0

The equation of the second line is

y = m₂x

∴  y = (1 – √3) x

 ∴  (1 – √3) x  – y = 0

Ans: The separate equations of the lines are  (1 + √3) x  – y = 0 and (1 – √3) x  – y = 0

Example 06:

• Obtain separate equations of lines represented by joint equation x² + 2(tanα) xy – y² = 0.
• Solution:

The given joint equation is x² + 2(tanα) xy – y² = 0

Dividing both sides of the equation by x²

The equation of a line passing through the origin is of the form y = mx

Substituting y/x = m in the equation (1) we get

1 + 2tanα m – m² = 0

∴  m² – 2tanα m – 1= 0

This is a quadratic equation in m and has two roots say m₁ and m₁

which gives slopes of the two lines represented by the joint equation.

a = 1, b = – 2tanα, c = -1

The roots are given by

The equation of the first line is

y = m₁x

∴  y = (tanα + secα) x

 ∴  (tanα + secα) x  – y = 0

The equation of the second line is

y = m₂x

∴  y = (tanα – secα) x

 ∴  (tanα – secα) x  – y = 0

Ans: The separate equations of the lines are  (tanα + secα) x  – y = 0 and  (tanα – secα) x  – y = 0

Example 07:

• Obtain separate equations of lines represented by joint equation x² + 2(cosecα) xy + y² = 0.
• Solution:

The given joint equation is x² + 2(cosecα) xy + y² = 0.

Dividing both sides of the equation by x²

The equation of a line passing through the origin is of the form y = mx

Substituting y/x = m in the equation (1) we get

1 + 2cosecα m + m² = 0

∴  m² + 2cosecα m + 1= 0

This is a quadratic equation in m and has two roots say m₁ and m₁

which gives slopes of the two lines represented by the joint equation.

a = 1, b = 2cosecα, c = 1

The roots are given by

The equation of the first line is

y = m₁x

∴  y = (- cosec α + cot α) x

∴  y = –  (cosec α – cot α) x

 ∴  (cosec α – cot α) x  – y = 0

The equation of the second line is

y = m₂x

∴  y = (- cosec α – cot α) x

∴  y = – (cosec α + cot α) x

 ∴  (cosec α + cot α) x  – y = 0

Ans: The separate equations of the lines are  (cosec α – cot α) x  – y = 0 and  (cosec α + cot α) x  – y = 0

Science > Mathematics > Pair of Straight Lines > Separate Equations of Lines (Auxillary Equation Method)