The slope of a Line

Science > Mathematics > Coordinate Geometry > Straight Lines > The slope of Line

In this article, we shall study to find the slope of line AB, when points A(x₁, y₁) and B(x₂, y₂) are given.

Type – I: To Find Slopeof a Line When Two Points on the Line are Given:

Example – 01:

Find the slopes of the lines which pass through the points

• (2, 5) and (-4, -4)

Let the points be A(2, 5) ≡ (x₁, y₁) and (-4, -4) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (- 4 – 5)/(- 4 – 2) = (-9)/(-6)

∴  Slope of line AB = 3/2

• (-2, 3) and (4, -6)

Let the points be A(-2, 3) ≡ (x₁, y₁) and (4, -6) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (- 6 – 3)/(4  + 2) = (-9)/(6)

∴  Slope of line AB = – 3/2

• (1, -3) and (-1, -1)

Let the points be A(1, -3) ≡ (x₁, y₁) and (-1, -1) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (- 1 + 3)/(- 1  – 1) = (2)/(-2)

∴  Slope of line AB = – 1

• (2, √3) and (3, 2√3)

Let the points be A(2, √3) ≡ (x₁, y₁) and (3, 2√3) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (2√3 – √3)/(3  – 2) = (√3)/(1)

∴  Slope of line AB = √3

• (3, 4) and (2, 5)

Let the points be A(3, 4) ≡ (x₁, y₁) and (2, 5) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (5 – 4)/(2 – 3) = (1)/(-1)

∴  Slope of line AB = – 1

• (2, 5) and (4, -6)

Let the points be A(2, 5) ≡ (x₁, y₁) and (4, -6) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (- 6 – 5)/(4  – 2) = (- 11)/(2)

∴  Slope of line AB = – 11/2

• (-1, 4) and (2, 2)

Let the points be A(-1, 4) ≡ (x₁, y₁) and (2, 2) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (2 – 4)/(2 + 1) = (-2)/(3)

∴  Slope of line AB = – 2/3

• (a, 0) and (0, b)

Let the points be A(a, 0) ≡ (x₁, y₁) and (0, b) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (b – 0)/(0 – a) = (b)/(-a)

∴  Slope of line AB = – b/a

• (at₁², 2at₁) and (at₂², 2at₂)

Let the points be A(at₁², 2at₁) ≡ (x₁, y₁) and (at₂², 2at₂) ≡ (x₂, y₂)

∴  Slope of line AB = (y₂ – y₁)/ (x₂ – x₁) = (2at₂ – 2at₁)/(at₂² – at₁²)

∴  Slope of line AB = 2a(t₂ – t₁)/a(t₂² – t₁²)

∴  Slope of line AB = 2(t₂ – t₁)/(t₂ + t₁)(t₂ – t₁)

∴  Slope of line AB = 2)/(t₂ + t₁)

• The origin, and the mid-point of the line segment joining the points P (0, – 4) and B (8, 0).

Midpoint of segment AB is M( (0 + 8)/2, (-4, 0)/2) = M(8/2, -4/2) = M(4, – 2)

Now slope of OM = (-2 – 0)/ (4 – 0) = -2/4 = – 1/2

Type – II: Find Value of Arbitrary Constant, When Slope is Given:

Example – 02:

Find the value of ‘k’ if the slope of the line passing through the points

• (2, 4), (5, k) is 5/3

Let the points be A(2, 4) and B(5, k)

Slope of AB = (k – 4)/(5 – 2) = 5/3

∴  (k – 4)/3 = 5/3

∴  k – 4 = 5

∴  k = 9

• (2, 5), (k, 3) is 2

Let the points be A(2, 5) and B(k, 3)

Slope of AB = (3 – 5)/(k – 2) = 2

∴  – 2  = 2k – 4

∴  2k = 2

∴  k = 1

• (k, 2), (-6, 8) is – 5/4

Let the points be A(k, 2) and B(-6, 8)

Slope of AB = (8 – 2)/(-6 – k) = -5/4

∴  6/(-6 – k) = -5/4

∴ 24 = 30 + 5k

∴ 5k = – 6

∴  k = – 6/5

Type – III: To Show Given Points are Collinear:

Example – 03:

By using slopes show that the following points are collinear.

• A(0,4), B(2,10) and C(3,13)

Given points are A(0,4), B(2,10) and C(3,13)

Slope of line AB = (10 – 4)/(2 – 0) = (6)/(2) = 3 …………. (1)

Slope of line BC = (13 – 10)/(3 – 2) = (3)/(1) = 3 …………. (2)

From equations (1) and (2)

Slope of line AB = Slope of line BC

B is common point

Hence points A, B and C are collinear

• P(5, 0), Q(10, -3) and R(-5, 6)

Given points are P(5, 0), Q(10, -3) and R(-5, 6)

Slope of line PQ = (-3 – 0)/(10 – 5) = (-3)/(5) = – 3/5 …………. (1)

Slope of line QR = (6 + 3)/(-5 – 10) = (9)/(- 15) = – 3/5 …………. (2)

From equations (1) and (2)

Slope of line PQ = Slope of line QR

Q is common point

Hence points P, Q and R are collinear

• L(2, 5), M(5, 7) and N(8, 9)

Given points are L(2, 5), M(5, 7) and N(8, 9)

Slope of line LM = (7 – 5)/(5 – 2) = (2)/(3) = 2/3 …………. (1)

Slope of line MN = (9 – 7)/(8 – 5) = (2)/(3) = 2/3 …………. (2)

From equations (1) and (2)

Slope of line LM = Slope of line MN

M is common point

Hence points L, M, and N are collinear

• D(5, 1), E(1, -1) and F(11, 4)

Given points are D(5, 1), E(1, -1) and F(11, 4)

Slope of line DE = (-1 – 1)/(1 – 5) = (-2)/(-4) = 1/2 …………. (1)

Slope of line EF = (4 + 1)/(11 – 1) = (5)/(10) = 1/2 …………. (2)

From equations (1) and (2)

Slope of line DE = Slope of line EF

E is common point

Hence points D, E, and F are collinear

Type IV: To Find Value of K if Given Points are Collinear:

Example – 04:

If the following points are collinear find value of k using slopes.

• (-2, -3), (k, 4) and (5, 5)

Let given points be A(-2, -3), B(k, 4) and C(5, 5)

Points A, B, and C are collinear

∴  Slope of line AB = Slope of line BC

∴  (4 + 3)/(k + 2) = (5 – 4)/(5 – k)

∴  7/(k + 2) = 1/(5 – k)

∴  7(5 – k) = 1(k + 2)

∴  35 – 7k = k + 2

∴  33 = 8k

∴  k = 33/8

• (5, k), (-3, 1) and (-7, -2)

Let given points be A(5, k), B(-3, 1) and C(-7, -2)

Points A, B, and C are collinear

∴  Slope of line AB = Slope of line BC

∴  (1 – k)/(-3 – 5) = (-2 – 1)/(-7 + 3)

∴  (1 – k)/(-8) = (-3)/(-4)

∴  (1 – k)/(-8) = (3/4)  x (-8)

∴  1 – k = – 6

∴  k = 7

• (2, 1), (4, 3) and (0, k)

Let given points be A(2, 1), B(4, 3) and C(0, k)

Points A, B, and C are collinear

∴  Slope of line AB = Slope of line BC

∴  (3 – 1)/(4 – 2) = (k – 3)/(0 – 4)

∴  2/2 = (k – 3)/(- 4)

∴ 1 (-4) = (k – 3)

∴  k – 3  = – 4

∴  k = – 1

• (-4, 5), (-3, 5) and (-1, k)

Let given points be A(-4, 5), B(-3, 5) and C(-1, k)

Points A, B, and C are collinear

∴  Slope of line AB = Slope of line BC

∴  (5 – 5)/(-3 + 4) = (k – 5)/(-1 + 3)∴  0/1 = (k – 5)/2

∴ 0 = (k – 5)/2

∴  k – 5  = 0

∴  k = 5

• (k, 1), (2, -3) and (3, 4)

Let given points be A(k, 1), B(2, -3) and C(3, 4)

Points A, B, and C are collinear

∴  Slope of line AB = Slope of line BC

∴  (-3 – 1)/(2 – k) = (4 + 3)/(3 – 2)

∴  (-4)/(2 – k) = 7/1

∴ -4 = 14 – 7k

∴  7k = 18

∴  k = 18/7

Type V: To Prove Given Condition When Collinearity of Points is Given:

Example – 05:

If three points (h, 0), (a, b) and (0, k) lie on a line, show that a/h + b/k = 1

Solution:

Let A(h, 0), B(a, b) and C(0, k) be the points lying on the line.

∴ Slope of AB = Slope of BC

∴ (b – 0)/(a – h) = (k – b)/(0 – a)

∴ b/(a – h) = (k – b)/(-a)

∴ – ab   = (a – h)(k – b)

∴  ak – kh + hb = 0

∴  ak + hb = kh

Dividing both sides of equation by kh

∴  ak/kh + hb/kh = kh/kh

∴  a/h + b/k = 1  (proved as required)

Example – 08:

A line passes through (x1, y1) and (h, k). If the slope of the line is m, show that k – y₁ = m (h – x₁).

Line passes through (x₁, y₁) and (h, k)

Slope of line = (k – y₁)/(h – x₁) = m

∴  k – y₁ = m (h – x₁)  (Proved as required)

Example – 09:

Three points P (h, k), Q (x₁, y₁) and R (x₂, y₂) lie on a line. Show that (h – x₁) (y₂ – y₁) = (k – y₁) (x₂ – x₁).

As the points lie on a line

Slope of line PQ = Slope of line QR

(k – y₁)/(h – x₁) = (y₂– y₁)/(x₂ – x₁)

∴ (k – y₁) (x₂ – x₁)= (h – x₁) (y₂ – y₁)

∴  (h – x₁) (y₂ – y₁) = (k – y₁) (x₂ – x₁)    (Proved)

Type – VI: Interpretation of Graph:

Example – 10:

Consider the following population and year graph, find the slope of the line AB, and using it, find what will be the population in the year 2010?

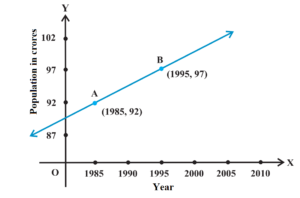
Solution:

Slope of line AB = (97 – 92)/(1995 -1985) = 5/10 = 1/2

Let the populatiomn in year 2010 be k

Thus point P(2010, k) lies on the line

Slope of AP = Slope of AB

Slope of AP = (k – 92)/(2010 – 1985) = 1/2

∴ (k – 92)/25 = 1/2

∴ 2k – 184 = 25

∴ 2k = 209

∴ k = 104.5

Hence population in 2010 will be 104.5 crore

Example – 11:

In the figure, the time and distance graph of linear motion is given. Two positions of time and distance are recorded as when T = 0, D = 2 and when T = 3, D = 8. Using the concept of slope, find the law of motion, i.e., how distance depends upon time.

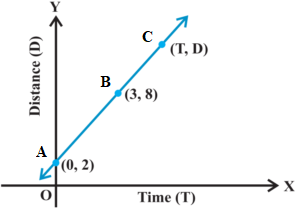
Slope of AB = Slope of BC

∴ (8 – 2)/(3 – 0) = (D – 8)(T – 3)

∴ 6/3 = (D – 8)(T – 3)

∴ 2 = (D – 8)(T – 3)

∴ 2(T – 3) = D – 8

∴ 2T – 6 = D – 8

∴ D = 2T – 6 + 8

∴ D = 2T + 2

This relation is known as the law of motion.

Science > Mathematics > Coordinate Geometry > Straight Lines > The slope of a Line