Science > Mathematics > Pair of Straight Lines > To Find the Condition When Relation Between Slopes is Given
In this article, we shall discuss problems to find the condition when the relation between slopes of lines represented by a joint equation is given.
Example – 18:
- If the slope of one of the lines given by ax2 + 2hxy + by2 = 0 is k times the slope of the other, prove that 4kh2 = ab(1+ k)2.
- Solution:
The given joint equation is ax2 + 2hxy + by2 = 0
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b, and m1 . m2 = a/b
Given the relation between slopes of lines
m1 = km2
Now, m1 + m2 = – 2h/b
∴ km2 + m2 =- 2h/b
∴ (k + 1)m2 =- 2h/b
∴ m2 = – 2h/b(k + 1)
Now, m1 . m2 = a/b
∴ km2 . m2 = a/b
∴ k(m2)2 = a/b
∴ (m2)2 = a/bk
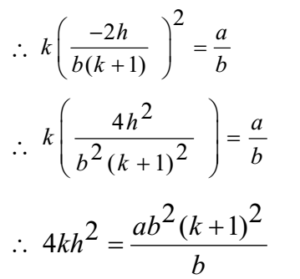
4kh2 = ab(1+ k)2 (proved as required)
Example – 19:
- If the slope of one of the lines given by ax2 + 2hxy + by2 = 0 is 5 times the slope of the other, prove that 5h2 = 9ab.
- Solution:
The given joint equation is ax2 + 2hxy + by2 = 0
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b, and m1 . m2 = a/b
Given the relation between slopes of lines
m1 = 5m2
Now, m1 + m2 = – 2h/b
∴ 5m2 + m2 =- 2h/b
∴ 6m2 =- 2h/b
∴ m2 = – h/3b
Now, m1 . m2 = a/b
∴ 5m2 . m2 = a/b
∴ 5(m2)2 = a/b
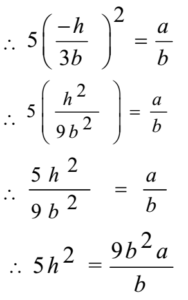
5h2 = 9ab (proved as required)
Example – 20:
- If the slope of one of the lines given by ax2 + 2hxy + by2 = 0 is 4 times the slope of the other, prove that 16h2 = 25ab.
- Solution:
The given joint equation is ax2 + 2hxy + by2 = 0
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b, and m1 . m2 = a/b
Given the relation between slopes of lines
m1 = 4m2
Now, m1 + m2 = – 2h/b
∴ 4m2 + m2 =- 2h/b
∴ 5m2 =- 2h/b
∴ m2 = – 2h/5b
Now, m1 . m2 = a/b
∴ 4m2 . m2 = a/b
∴ 4(m2)2 = a/b
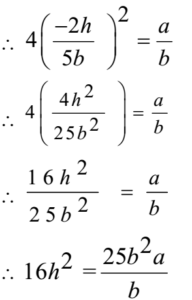
16h2 = 25ab (proved as required)
Example – 21:
- If the slope of one of the lines given by ax2 + 2hxy + by2 = 0 is 3 times the slope of the other, prove that 3h2 = 4ab.
- Solution:
The given joint equation is ax2 + 2hxy + by2 = 0
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b, and m1 . m2 = a/b
Given the relation between slopes of lines
m1 = 3m2
Now, m1 + m2 = – 2h/b
∴ 3m2 + m2 =- 2h/b
∴ 4m2 =- 2h/b
∴ m2 = – h/2b
Now, m1 . m2 = a/b
∴ 3m2 . m2 = a/b
∴ 3(m2)2 = a/b

3h2 = 4ab (proved as required)
Example – 22:
- Find the condition that slope of one of the lines represented by ax2 + 2hxy + by2 = 0 is square of the slope of another line.
- Solution:
The given joint equation is ax2 + 2hxy + by2 = 0
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b, and m1 . m2 = a/b
Given the relation between slopes of lines
m1 = (m2)2
Now, m1 . m2 = a/b
∴ (m2)2 . m2 = a/b
∴ (m2)3 = a/b
Now, m1 + m2 = – 2h/b
∴ (m2)2 + m2 = – 2h/b
Making cube of both sides
((m2)2 + m2)3 = (- 2h/b)3

Multiplying both sides by b3
a2b – 6abh + ab2 = -8h3
a2b + ab2 + 8h3 = 6abh
This is the required condition
Example – 23:
- Show that one of the straight line given by ax2 + 2hxy + by2 = 0 bisects an angle between the co-ordinate axes if and only if (a + b)2 = 4h2.
- Solution:
The given joint equation is ax2 + 2hxy + by2 = 0
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b, and m1 . m2 = a/b
Now given that One of the straight line represented by the joint equation bisects the angle between the co-ordinate axes. Thus the slope of the line is ± 1. let m2 = ± 1


Example – 24:
- If the straight lines represented by a joint equation ax2 + 2hxy + by2 = 0 make angles of equal measures with the co-ordinate axes. Then prove that a = ± b.
- Solution:
Let α be the angle made by the lines with coordinate axes.

Let OA be the line making an angle α with the x-axis and
OB be the line making an angle α with y-axis.
The angle made by the line with the positive direction of x-axis is α. Hence its slope is
m1 = tan α
The angle made by OB with the positive direction of x-axis is (π/2 ± α). Hence its slope is
m2 = tan (π/2 ± α) = ± cot α
The given joint equation is ax2 + 2hxy + by2 = 0
Let m1 and m2 be the slopes of the two lines represented by given joint equation
(m1 + m2) = – 2h/b, and m1 . m2 = a/b
