To Find Value of Constant When Relation Between Slopes is Given

Science > Mathematics > Pair of Straight Lines > To Find Value of Constant When Relation Between Slopes is Given

In this article, we shall study to solve problems to find the value of constant or to prove the given relation when the relation between slopes of the line represented by the joint equation is given.

Remember:

• If m₁ and m₂ are the slopes of the two lines represented by joint equation  ax² + 2hxy  + by² = 0. Then m₁. m₂ = a/b ; m₁ + m₂ = -2h/b  and remember (m₁ – m₂) 2 =  (m₁+ m₂)² – 4m₁.m₂.

Algorithm:

1. Write given of joint equation.
2. Compare with the standard equation.
3. Find values of a, h and b.
4. Use above relations between slopes
5. Solve equations and get the value of constant

Example – 01:

• Show that the equation 3x² – 4xy +  y² = 0 represents the pair of lines whose slopes differ by 2.
• Solution:

The given joint equation is 3x² – 4xy + y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 3, 2h = – 4, and b = 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = -(-4)/1 = 4 and  m₁ . m₂ = a/b = 3/1 = 3

Using  (m₁ – m₂)² =  (m₁ + m₂)² –  4 m₁ . m₂

∴   (m₁ – m₂)² =  (4)² –  4 (3)

∴   (m₁ – m₂)² =  16 – 12

∴   (m₁ – m₂)² =  4

Taking square roots of both sides we get,

| m₁ – m₂| = 2

Hence the slopes differ by 2.

Example – 02:

• Show that the equation 77x² – 36xy +  4y² = 0 represents the pair of lines whose slopes differ by 2.
• Solution:

The given joint equation is 77x² – 36xy +  4y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 77, 2h = – 36, and b = 4

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = -(-36)/4 = 9 and  m₁ . m₂ = a/b = 77/4

Using  (m₁ – m₂)² =  (m₁ + m₂)² –  4 m₁ . m₂

∴   (m₁ – m₂)² =  (9)² –  4 (77/4)

∴   (m₁ – m₂)² =  81 – 77

∴   (m₁ – m₂)² =  4

Taking square roots of both sides we get,

| m₁ – m₂| = 2

Hence the slopes differ by 2.

Example – 03:

• Show that the difference of the slopes of the two lines represented by equation x²(tan²θ + cos²θ)  – 2xy tanθ + y²sin²θ = 0 is 2.
• Solution: 

The given joint equation is x²(tan²θ + cos²θ)  – 2xy tanθ + y²sin²θ = 0

Comparing with ax² + 2hxy + by² = 0

Here a = (tan²θ + cos²θ), 2h = – 2tanθ, and b = sin²θ

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = -(- 2tanθ)/sin²θ = 2tanθ)/sin²θ

and  m₁ . m₂ = (tan²θ + cos²θ)/sin²θ

Using  (m₁ – m₂)² =  (m₁ + m₂)² –  4 m₁ . m₂

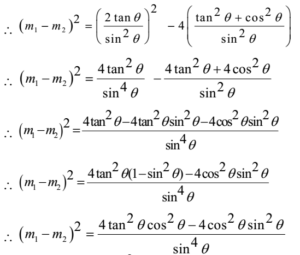
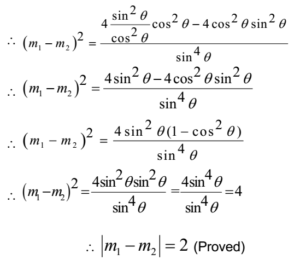
Hence the slopes differ by 2.

Example – 04:

• Show that the difference of the slopes of the two lines represented by equation (tan²θ + 3)(tan²θ – 1)x² – 2xy sec²θ   +  y² = 0 is 4.
• Solution:

The given joint equation is (tan²θ + 3)(tan²θ – 1)x² – 2xy sec²θ   +  y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = (tan²θ + 3)(tan²θ – 1), 2h = – 2sec²θ, and b = 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = -(- 2sec²θ)/1 =  2sec²θ

and  m₁ . m₂ = (tan²θ + 3)(tan²θ – 1)/1 = (tan²θ + 3)(tan²θ – 1)

Using  (m₁ – m₂)² =  (m₁ + m₂)² –  4 m₁ . m₂

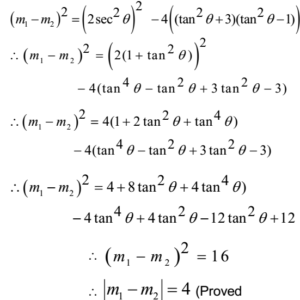
Hence the slopes differ by 4.

Example – 05:

• Find λ, if the difference of the slopes of the lines λx² + 6xy –  4y² = 0 is equal to their product.
• Solution:

The given joint equation is λx² + 6xy –  4y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = λ, 2h = 6, and b = – 4

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = -6/-4 = 3/2 and  m₁ . m₂ = a/b = λ/-4  = – λ/4

Given the relation between slopes

| m₁ – m₂| = m₁ . m₂

squaring both sides

 (m₁ – m₂)² =  (m₁ . m₂)²

 ∴   (m₁ + m₂)² –  4 m₁ . m₂=  (m₁ . m₂)²

∴   (3/2)² –  4 (- λ/4)=  (- λ/4)²

∴   9/4 +  λ =  λ²/16

Multiplying both sides of equation by 16

∴   36 +  16λ =  λ²

∴  λ² –  16λ  – 36 =  0

∴  (λ – 18)(λ + 2) =  0

∴   λ = 18 or λ = – 2

Example – 06:

• Find k, if the difference of the slopes of the lines  3x² + kxy  – y² = 0 is 4.
• Solution:

The given joint equation is 3x² + kxy  – y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 3, 2h = k, and b = – 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = -k/-1 = k and  m₁ . m₂ = a/b  = 3/-1 = – 3

Given the relation between slopes

| m₁ – m₂| = 4

squaring both sides

 (m₁ – m₂)² = 16

 ∴   (m₁ + m₂)² –  4 m₁ . m₂=  16

∴   (k)² –  4 (- 3)=  16

∴   k² + 12 =  16

∴   k²  = 4

∴   k = ± 2

Example – 07:

• Find k if the slopes of lines given by kx² + 5xy  + y² = 0 differ by 1.
• Solution:

The given joint equation is kx² + 5xy  + y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = k, 2h = 5, and b = 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – 5/1 = – 5 and  m₁ . m₂ = a/b = k/1 = k

Given the relation between slopes

| m₁ – m₂| = 1

squaring both sides

 (m₁ – m₂)² = 1

 ∴   (m₁ + m₂)² –  4 m₁ . m₂= 1

 ∴   (-5)² –  4 k=  1

∴  25 –  4 k=  1

∴   –  4 k=  – 24

∴   k = 6

Example – 08:

• Find k, if the slope of one of the lines given by kx² + 4xy  – y² = 0 exceeds the slope of other by 8.
• Solution:

The given joint equation is kx² + 4xy  – y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = k, 2h = 4, and b = – 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – 4/-1 =  4 and  m₁ . m₂ = a/b  = k/-1 = – k

Given the relation between slopes

| m₁ – m₂| = 8

squaring both sides

 (m₁ – m₂)² = 64

 ∴   (m₁ + m₂)² –  4 m₁ . m₂= 64

 ∴   (4)² –  4(- k)=  64

∴  16 +  4 k=  64

∴   – 4 k= 48

∴   k = 12

Example – 09:

• Find k, if the difference between the slopes of the lines  12x² + k xy  – y² = 0 is 7.
• Solution:

The given joint equation is 12x² + k xy  – y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 12, 2h = k, and b = – 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – k/-1 = k and  m₁ . m₂ = a/b = 12/-1 = – 12

Given the relation between slopes

| m₁ – m₂| = 7

squaring both sides

 (m₁ – m₂)² = 49

 ∴   (m₁ + m₂)² –  4 m₁ . m₂= 49

 ∴   (k)² –  4(- 12)=  49

 ∴   k² + 48 =  49

∴  k² = 1

∴   k = ± 1

Example – 10:

• Find k, if the slope of one of the lines given by 3x² + 4xy  + ky² = 0 is three times the slope of the other.
• Solution:

The given joint equation is 3x² + 4xy  + ky² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 3, 2h = 4, and b = k

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – 4/k and  m₁ . m₂ = a/b = 3/k

Given the relation between slopes

m₁ = 3m₂

∴  k² = k

∴  k² – k = 0

∴  k (k – 1) = 0

∴  k = 0 and k = 1

But k cannot be zero.

∴ k = 1

Example – 11:

• Find k, if the slope of one of the lines given by kx² + 4xy  – y² = 0 is three times the slope of the other.
• Solution:

The given joint equation is kx² + 4xy  – y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = k, 2h = 4, and b = – 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – 4/-1 = 4, and  m₁ . m₂ = a/b = k/-1 = – k

Given the relation between slopes

m₁ = 3m₂

Now, m₁ + m₂ = 4

∴  3m₂ + m₂ = 4

∴  4m₂ = 4

∴  m₂ = 1

∴  m₁ = 3m₂ = 3 x 1 = 3

Now, m₁ . m₂ =  – k

∴  (3)(1) = – k

∴  k = – 3

Example – 12:

• Find k, if the slope of one of the lines given by 4x² + kxy  + y² = 0 is four times the slope of the other.
• Solution:

The given joint equation is 4x² + kxy  + y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 4, 2h = k, and b = 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – k/1 = – k, and  m₁ . m₂ = a/b = 4/1 = 4

Given the relation between slopes

m₁ = 4m₂

Now, m₁ + m₂ = – k

∴  4m₂ + m₂ = – k

∴  5m₂ = – k

∴  m₂ = – k/5

Now, m₁ . m₂ = 4

∴  4m₂ . m₂ = 4

∴  (m₂)² = 1

∴  (- k/5)² = 1

∴  (- k/5) = ± 1

∴  k = ± 5

Example – 13:

• Find k, if the slope of one of the lines given by 5x² + kxy  + y² = 0 is five times the slope of the other.
• Solution:

The given joint equation is 5x² + kxy  + y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 5, 2h = k, and b = 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – k/1 = – k, and  m₁ . m₂ = a/b = 5/1 = 5

Given the relation between slopes

m₁ = 5m₂

Now, m₁ + m₂ = – k

∴  5m₂ + m₂ = – k

∴  6m₂ = – k

∴  m₂ = – k/6

Now, m₁ . m₂ = 5

∴  5m₂ . m₂ = 5

∴  (m₂)² = 1

∴  (- k/6)² = 1

∴  (- k/6) = ± 1

∴  k = ± 6

Example – 14:

• Find k if the sum of the slopes of lines given by kx² + 8xy + 5 y² = 0 is twice the product of the slopes.
• Solution:

The given joint equation is kx² + 8xy + 5 y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = k, 2h = 8, and b = 5

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – 8/5, and  m₁ . m₂ = a/b = k/5

Given the relation between slopes

m₁ + m₂ = 2 m₁ . m₂

-8/5 = 2 x k/5

∴  k = – 4

Example – 15:

• Find k if the sum of the slopes of lines given by 2x² + kxy -3y² = 0 is equal to the product of the slopes.
• Solution:

The given joint equation is 2x² + kxy -3y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 2, 2h = k, and b = -3

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – k/-3 = k/3, and  m₁ . m₂ = a/b = 2/-3 = – 2/3

Given the relation between slopes

m₁ + m₂ = m₁ . m₂

k/3 = (-2/3)

∴  k = – 2

Example – 16:

• Find k, if the sum of the slopes of lines given by 3x² + kxy  + y² = 0 is zero.
• Solution:

The given joint equation is 2x² + kxy -3y² = 0

Comparing with ax² + 2hxy + by² = 0

Here a = 3, 2h = k, and b = 1

Let m₁ and m₂ be the slopes of the two lines represented by given joint equation

 (m₁ + m₂) = – 2h/b = – k/1 = – k, and  m₁ . m₂ = a/b = 3/1 = 3

Given the relation between slopes

m₁ + m₂ = 0

∴  – k = 0

∴  k = 0

Example – 17:

• Find k, if the slope of one of the lines given by 3x² – 4xy  + ky² = 0 is 1.
• Solution:

Given joint equation of lines is 3x² – 4xy  + ky² = 0

It is in the form ax² + 2hxy  + by² = 0.

a = 3, 2h = – 4 and b= k

The auxiliary equation of given line is of the form

bm² + 2hm + a = 0

∴   km² – 4m + 3 = 0   ……… (1)

Slope of one of the line is 1

Substituting m = 1 in equation (1) we get

k(1)² – 4(1) + 3 = 0

∴   k – 1 = 0

∴   k = 1

Science > Mathematics > Pair of Straight Lines > To Find Value of Constant When Relation Between Slopes is Given