Angle Measurement

Science > Mathematics > Trigonometry > Angle Measurement > Angle Measurement

In this article, we shall study the problems based on the interior angles of a polygon, and the angle between the hour hand and a minute hand of a clock.

Example – 01:

If x^c = 405° and y° = – (π/12)^c. Find x and y

Solution:

Given x^c = 405°

x containing term on R.H.S. is in radians. Hence we should convert L.H.S. into radians

∴  x^c = 405° = 405 x π/180 = (9π/4)^c

∴  x = 9π/4

Given y° = – (π/12)^cy containing term on R.H.S. is in degrees. Hence we should convert L.H.S. into degrees

∴  y° = – (π/12)^c = – (π/12) x (180/π) = 15°

∴  y = 15

Ans: x = 9π/4 and y = 15

Example – 02:

If θ° = – (5π/9)^c and Φ^c = 900°. Find θ and Φ

Solution:

Given θ° = – (5π/9)^c

θ containing term on R.H.S. is in degrees. Hence we should convert L.H.S. into degrees

∴  θ° = – (5π/9)^c = – (5π/9) x (180/π) = – 100°

∴  θ = -100

Given Φ^c = 900°

Φ containing term on R.H.S. is in radians. Hence we should convert L.H.S. into radians

∴  Φ^c = 900° = 900 x π/180 = (5π)^c

∴  Φ = 5π

Ans: θ = -100 and Φ = 5π

Example – 03:

Express following angles in radians

– 35°45’30”

Solution:

– 35°45’30” = – [35° + (45/60)° + (30/3600)°]

– 35°45’30” = – [35° + 0.75° + 0.0083°] = – 35.7583°

– 35°45’30” = – 35.7583 x π/180 = 0.1987 π

– 35°45’30” = 0.1987 x 3.142 = 0.6242 radian

50°37’30”

Solution:

50°37’30” = 50° + (37/60)° + (30/3600)°

50°37’30” = 50° + 0.6167° + 0.0083° = 50.625°

50°37’30” = 50.625 x π/180 = 0.2812 π

50°37’30” = 0.2812 x 3.142 = 0.8837 radian

– 10°40’30”

Solution:

10°40’30” = 10° + (40/60)° + (30/3600)°

10°40’30” = 10° + 0.6667° + 0.0083° = 10.675°

10°40’30” = 10.675 x π/180 = 0.0593 π

10°40’30” = 0.0593 x 3.142 = 0.1863 radian

Interior Angle of Regular Polygon:

Steps to Find Interior Angle of Polygon:

1. Find the measure of each exterior angle of regular polygon = 360°/No.of sides of polygon
2. Find the measure of each interior angle of polygon = 180° – measure of exterior angle

Example – 04:

Find Interior angles of following regular polygons in degrees and radians

Pentagon:

Solution:

Pentagon has 5 sides

Each exterior angle  = 360°/5 = 72°

Each interior angle = 180° – 72° = 108° = 108 x π/180 = (3π/5)^c

Ans: The interior angle of a regular pentagon is 72° or (3π/5)^c

Hexagon:

Solution:

Hexagon has 6 sides

Each exterior angle  = 360°/6 = 60°

Each interior angle = 180° – 60° = 120° = 120 x π/180 = (2π/3)^c

Ans: The interior angle of a regular hexagon is 120° or (2π/3)^c

Octagon:

Solution:

Octagon has 8 sides

Each exterior angle  = 360°/8 = 45°

Each interior angle = 180° – 45° = 135° = 135 x π/180 = (3π/4)^c

Ans: The interior angle of a regular octagon is 135° or (3π/4)^c

A Polygon with 20 sides:

Solution:

Polygon has 20 sides

Each exterior angle  = 360°/20 = 18°

Each interior angle = 180° – 18° = 162° = 162 x π/180 = (9π/10)^c

Ans: The interior angle of a regular polygon with 20 sides is 162° or (9π/10)^c

A Polygon with 15 sides:

Solution:

Polygon has 15 sides

Each exterior angle  = 360°/15 = 24°

Each interior angle = 180° – 24° = 156° = 156 x π/180 = (13π/15)^c

Ans: The interior angle of a regular polygon with 15 sides is 156° or (13π/15)^c

A Polygon with 12 sides:

Polygon has 12 sides

Each exterior angle  = 360°/12 = 30°

Each interior angle = 180° – 30° = 150° = 150 x π/180 = (5π/6)^c

Ans: The interior angle of a regular polygon with 12 sides is 150° or (5π/6)^c

Example – 05:

Find the number of sides of polygon if each of its interior angle is (3π/4)^c.

Solution:

Each interior angle = (3π/4)^c = (3π/4) x (180/π) = 135°

Hence each exterior angle = 180° – 135° = 45°

Number of sides of polygon = 360°/each exterior angle = 360°/45 = 8°

Ans: Thus the polygon has 8 sides

Angle Between Hour Hand and Minute Hand:

Example – 06:

Find the degree and radian measure of the angle between the hour hand and minute hand of a clock at the following timings.

Twenty minutes past seven:

Solution:

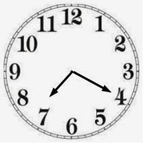
At twenty minutes past seven, the minute hand is at 4 and hour hand crossed 7

Angle traced by hour hand in 1 minute = 0.5°

Angle traced by hour hand in 20 minutes = 0.5° x 20 = 10°

Thus the hour hand is 10° ahead of 7 th Mark

The angle between 4 and 7 is 90°

Thus angle between hour hand and minute hand = 90° + 10° = 100°

100° = 100 x π/180 = (5π/9)^c

Ans: The angle between the hour hand and the minute hand is 100° or (5π/9)^c

Twenty minutes past two:

Solution:

At twenty minutes past two, the minute hand is at 4 and hour hand crossed 2

Angle traced by hour hand in 1 minute = 0.5°

Angle traced by hour hand in 20 minutes = 0.5° x 20 = 10°

Thus the hour hand is 10° ahead of 2 nd Mark

The angle between 2 and 4 is 60°

Thus angle between hour hand and minute hand = 60° – 10° = 50°

50° = 50 x π/180 = (5π/18)^c

Ans: The angle between the hour hand and the minute hand is 50° or (5π/18)^c

Quarter past six:

Solution:

At quarter past six, the minute hand is at 3 and hour hand crossed 6

Angle traced by hour hand in 1 minute = 0.5°

Angle traced by hour hand in 15 minutes = 0.5° x 15 = 7.5°

Thus the hour hand is 7.5° ahead of 6th Mark

The angle between 3 and 6 is 90°

Thus angle between hour hand and minute hand = 90° + 7.5° = 97.5°

97.5° = 97.5 x π/180 = (13π/24)^c

Ans: The angle between the hour hand and the minute hand is 97.5° or (13π/24)^c

Ten past eleven:

Solution:

At ten past eleven, the minute hand is at 2 and hour hand crossed 11

Angle traced by hour hand in 1 minute = 0.5°

Angle traced by hour hand in 10 minutes = 0.5° x 10 = 5°

Thus the hour hand is 5° ahead of 11th Mark

The angle between 11 and 2 is 90°

Thus angle between hour hand and minute hand = 90° – 5° = 85°

85° = 85 x π/180 = (17π/36)^c

Ans: The angle between the hour hand and the minute hand is 85° or (17π/36)^c

Example – 07:

Show that the minute hand of a clock gains 5°30′ on hour hand in one minute.

Solution:

Angle traced by hour hand in 1 minute = 0.5°

Angle traced by minute hand in 1 minute = 6°

Thus angle between hour hand and minute hand = 6° – 0.5° = 5.5° = 5°30′

Ans: Thus the minute hand of a clock gains 5°30′ on hour hand in one minute.

Example – 08:

Determine which of the following pairs of angles are coterminal.

210° and – 150°

– 150° = – 150° + 360° = 210°

Thus the two angles have the same initial arm and terminal arm.

Hence the angles 210° and – 150° are coterminal angles.

330° and – 60°

– 60° = – 60° + 360° = 300°

Thus the two angles do not have the same initial arm and terminal arm.

 Hence the angles 330° and – 60° are not coterminal angles.

405° and – 675°

405° = 405° – 360° = 45°

– 675° + 360° x 2 = 45°

Thus the two angles have the same initial arm and terminal arm.

 Hence the angles 405° and – 675° are coterminal angles.

1230° and – 930°

1230° = 1230° – 360° x 3 = 150°

– 930° + 360° x 3 = 150°

Thus the two angles have the same initial arm and terminal arm.

 Hence the angles 1230° and – 930° are coterminal angles.

Example – 09:

A wheel makes 360 revolutions in one minute. Through how many radians does it turn in 1 second?

Given: No. of revolutions = 360 per minute

To Find: Radians per second =?

Solution:

No. of revolutions per second = 360/60 = 6

In one revolution the wheel turns through 2π radians

Radians per second = 2π x 6 = 12π^c

Ans: The wheel will turn through 12π^c in 1 second

Science > Mathematics > Trigonometry > Angle Measurement > Angle Measurement