Length of an Arc

Science > Mathematics > Trigonometry > Angle Measurement > Length of an Arc

In this article, we shall solve problems based on the length of an arc (arc length).

Example – 01:

Find the length of the arc of a circle of diameter 10 cm, if the arc is subtending an angle of 36° at the centre.

Given: Diameter = 10 cm, radius = r = 10/2 = 5 cm, angle subtended = 36° = 36 x (π/180) = (π//5)^c

To Find: Length of arc = S = ?

Solution:

length of arc is given by

S = r θ  = 5 x (π//5) = π cm

Ans: The length of the arc is π cm

Example – 02:

Find the length of the arc of a circle which subtends an angle of 108° at the centre, if the radius of the circle is 15 cm.

Given: radius = r = 15 cm, angle subtended = 108° = 108 x (π/180) = (3π//5)^c

To Find: Length of arc = S = ?

Solution:

length of arc is given by

S = r θ  = 15 x (3π//5) = 9π cm

Ans: The length of the arc is 9π cm

Example – 03:

The radius of a circle is 9 cm. Find the length of an arc of this circle which cuts off a chord of length equal to the length of the radius.

Given: radius = r = 9 cm, length of chord = r

To Find: Length of arc = S = ?

Solution:

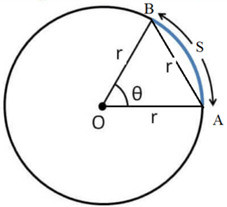
Thus ΔOAB is equilateral triangle

angle subtended = 60° = 60 x (π/180) = (π//3)^c

We have

S = r θ  = 9 x π//3 = 3π cm

Ans: The length of the arc is 3π cm

Example – 04:

In a circle of diameter 40 cm, the length of the chord is 20 cm. Find the length of the minor arch of the chord.

Given: diameter = 4o cm, radius = r = 20 cm, length of chord = 20 cm

To Find: Length of arc = S = ?

Solution:

Thus ΔOAB is equilateral triangle

angle subtended = 60° = 60 x π/180 = (π//3)^c

We have

S = r θ  = 20 x π//3 = 20π/3 cm

Ans: The length of the minor arc is 20π/3 cm

Example – 05:

A pendulum of 14 cm long oscillates through an angle of 18°. Find the length of the path described by its extremity.

Given: radius = r = 14 cm, angle subtended = 18° = 18 x (π/180) = (π//10)^c

To Find: Length of arc = S = ?

Solution:

We have

S = r θ  = 14 x π/10 = 1.4π cm

Ans: The length of arc is 1.4π cm

Example – 06:

Find in radians and degrees the angle subtended at the centre of a circle by an arc whose length is 15 cm, if the radius of circle is 25 cm.

Given: radius = r = 25 cm, Length of arc = 15 cm

To Find: angle subtended at the centre = θ = ?

Solution:

We have

S = r θ

∴  θ = S/r = 15/25 = (3/5)^c

(3/5)^c = (3/5) x (180/π) = (108/π)°

Ans: The angle subtended at the centre is (3/5)^c or (108/π)°

Example – 07:

Find the radius of the circle in which a central angle of 60° intercepts an arc of length 37.4 cm. Take ( π = 22/7)

Given: Length of arc = S = 37.4 cm, angle subtended = 60° = 60 x π/180 = (π//3)^c

To Find: Length of arc = S = ?

Solution:

We have

S = r θ

∴   r =S/θ = 37.4/(π//3) = (37.4 x 3) / (22/7)

∴   r = (37.4 x 3 x 7) / 22 = 35.7

Ans: The length of the arc is 35.7 cm

Example – 08:

A wire of length 10 cm is bent so as to form an arc of a circle of radius 4 cm. What is the angle subtended at the centre in degrees?

Given: radius = r = 4 cm, length of wire = length of arc = 10 cm

To Find: angle subtended at the centre = θ = ?

Solution:

We have

S = r θ

∴  θ = S/r = 10/4 = (2.5)^c

(2.5)^c = (2.5) x (180/π) = (450/π)

Ans: The angle subtended at the centre is (2.5)^c or (450/π)°

Example – 09:

Δ PQR is an equilateral triangle with a side 18 cm. A circle is drawn on segment QR as a diameter. Find the length of the arc of this circle intercepted within the triangle.

Given: Side of equilateral triangle = 18 cm, radius = 18/2 = 9 cm

To Find: length of the arc of circle intercepted = S =?

Solution:

s Δ PQR is an equilateral triangle, its each angle is 60°

Hence the triangles Δ QOE and Δ ROD are also equilateral triangles

∠ EOQ = ∠ ROD = 60°

EOD = 60° =  θ

Now, we have

S = r θ  = 9 x π//3 = 3π cm

Ans: The length of arc is 3π cm

Example – 10:

Two arcs of the same length subtend angle 60° and 75° at the centres of the circles. What is the ratio of the radii of the two circles?

Given: Angles subtended, θ₁ = 60° and θ₂ = 75°

To Find: Ratio of radii = r₁/r₂ = ?

Solution:

length of arc is given by S = r θ

For the first arc S₁ = r₁θ₁  ………. (1)

For the second arc S₂ = r₂θ₂  ………. (2)

Now length of two arcs is the same

S₁ = S₂

∴  r₁θ₁ =  r₂θ₂

∴  r₁/r₂ =  θ₂/ θ₁

∴  r₁/r₂ =  75°/ 60° = 5/4

Ans: The ratio of radii is 5:4

Example – 11:

Two arcs of the same length subtend angle 65° and 110° at the centres of the circles. What is the ratio of the radii of the two circles?

Given: Angles subtended, θ₁ = 65° and θ₂ = 110°

To Find: Ratio of radii = r₁/r₂ = ?

Solution:

length of arc is given by S = r θ

For the first arc S₁ = r₁θ₁  ………. (1)

For the second arc S₂ = r₂θ₂  ………. (2)

Now length of two arcs is the same

S₁ = S₂

∴  r₁θ₁ =  r₂θ₂

∴  r₁/r₂ =  θ₂/ θ₁

∴  r₁/r₂ =  110°/ 65° = 22/13

Ans: The ratio of radii is 22:13

Example – 12:

A train is running on a circular track of a radius of 1 km at a rate of 36 km per hour. Find the angle to the nearest minute, through which it will turn in 30 seconds.

Given: Radius of the arc = r = 1 km = 1000 m, Speed of train = v = 36 km per hour = 36 x 1000/3600 = 10 m/s, time taken = t = 30 s.

To Find: Angle through which the train turns = θ = ?

Solution:

Distance covered by train  i.e. length of arc =  speed x time = 10 x 30 = 300 m

S = r θ

∴  θ = S/r = 300/1000 = (0.3)^c

∴  θ = (0.3)^c = (0.3) x (180/π) = (54/3.142)° = 17.19°

∴  θ = 17° + 0.19° = 17° + 0.19 x 60′ = 17° + 11′ = 17°,11′

Ans: The train will turn through 17°,11′

Example – 13:

A train is running on a circular track of a radius of 1500 m at the rate of 66 km per hour. Find the angle to the in radian, through which it will turn in 10 seconds.

Given: Radius of the arc = r = 1500 m, Speed of train = v = 66 km per hour = 66 x 1000/3600 = 55/3 m/s, time taken = t = 10 s.

To Find: Angle through which the train turns = θ = ?

Solution:

Distance covered by train  i.e. length of arc =  speed x time = (55/3) x 10 = 550/3 m

S = r θ

∴  θ = S/r = (550/3)/1500 = 550/4500 = (11/90)^c

Ans: The train will turn through (11/90)^c

Example – 14:

A horse is tied to a post by a rope. If the horse moves along a circular path, always keeping the rope tight and describes 88 m when it traces an angle of 72° at the centre, find the length of the rope. Take π = 22/7.

Given: central angle = θ = 72° = 72 x π/180 = (2π/5)^c, arc length = S = 88 m

To Find: Length of rope = r = ?

S = r θ

∴  r = S/θ = 88/(2π/5) = 220/π = 220 x 7/22 = 70 m

Ans: The length of the rope is 70 m.

Example – 15:

If the perimeter of a sector of a circle is four times the radius of the circle, find the central angle of the corresponding sector in radians.

Given:  Perimeter = 4 x radius = 4r

To find: Central angle = θ = ?

Perimeter of sector = r + r + s = 4r

∴ 2r + r θ = 4r

∴ r θ = 2r

∴   θ = 2^c

Ans: The central angle  is 2^c

Science > Mathematics > Trigonometry > Angle Measurement > Length of an Arc