Use of Trigonometric Functions Values of Standard Angles

In this article, we shall study to find the value of trigonometric expressions involving standard angles. Trigonometric functions values of some standard angles are given below:

Evaluate the following:

Example 01:

sin²0^c + sin²(π/6)^c + sin²(π/3)^c + sin²(π/2)^c  

= (0)² + (1/2)² + (√3/2)² + (1)²

= 0 + 1/4 + 3/4 + 1 = 1+ 1 = 2

Ans: sin²0^c + sin²(π/6)^c + sin²(π/3)^c + sin²(π/2)^c = 2

Example 02:

cos²0 + cos²(π/6)^c + cos²(π/3)^c + cos²(π/2)^c  

= (1)² + (√3/2)² + (1/2)² + (0)²

= 1 + 3/4 + 1/4 + 0 = 1+ 1 = 2

Ans: cos²0 + cos²(π/6)^c + cos²(π/3)^c + cos²(π/2)^c = 2

Example 03:

sin (π)^c + 2 cos (π)^c + 3 sin (3π/2)^c + 4 cos (3π/2)^c – 5 sec (π)^c + 6 cosec (π/2)^c

=  (0) + 2(-1) + 3(-1) + 4 (0) – 5 (-1) + 6 (1)

= 0 – 2 – 3 + 5 + 6 =  6

Ans: sin (π)^c + 2 cos (π)^c + 3 sin (3π/2)^c + 4 cos (3π/2)^c – 5 sec (π)^c + 6 cosec (π/2)^c = 6

Example 04:

sin (0)^c + 2 cos (0)^c + 3 sin (π/2)^c + 4 cos (π/2)^c + 5 sec (0)^c + 6 cosec (π/2)^c

= 0 + 2 (1) + 3 (1) + 4 (0) + 5 (1) + 6 (1)

= 2 + 3 + 0 + 5 + 6 = 16

Ans: sin (0)^c + 2 cos (0)^c + 3 sin (π/2)^c + 4 cos (π/2)^c + 5 sec (0)^c + 6 cosec (π/2)^c = 16

Example 05:

4 cot 45° – sec² 60° + sin² 30°

= 4 (1) – (2)² + (1/2)² 

=  4  – 4 + 1/4  = 1/4

Ans: 4 cot 45° – sec² 60° + sin² 30° = 1/4

Verify the Following:

Example 06:

• cot² 60° + sin² 45° + sin² 30° + cos² 90° = 13/12
• Solution:

L.H.S. = cot² 60° + sin² 45° + sin² 30° + cos² 90°

∴ L.H.S. = (1/√3)²  + (1/√2)² + (1/2)² + (0)²

∴ L.H.S. =  1/3 + 1/2 + 1/4 = 5/6 + 1/4

∴ L.H.S. = 26/24 = 13/12 = R.H.S.

∴   cot² 60° + sin² 45° + sin² 30° + cos² 90° = 13/12  (Proved)

Example 07:

• sin² 30° + cos² 60° + tan² 45° + sec² 60°  – cosec² 30° = 3/2
• Solution:

L.H.S. = sin² 30° + cos² 60° + tan² 45° + sec² 60°  – cosec² 30°

∴ L.H.S. = (1/2)²  + (1/2)² + (1)²  + (2)² – (2)²

∴ L.H.S. =  1/4 + 1/4 + 1 + 4 – 4 = 2/4 +1

∴ L.H.S. = 1/2 + 1 = 3/2  = R.H.S.

∴  sin² 30° + cos² 60° + tan² 45° + sec² 60°  – cosec² 30° = 3/2   (Proved)

Example 08:

• 4 cot² 30° + 9 sin² 60° – 6 cosec² 60°  -(9/4) tan² 60° = 4
• Solution:

L.H.S. = 4 cot² 30° + 9 sin² 60° – 6 cosec² 60°  – (9/4) tan² 60°

∴ L.H.S. = 4 (√3)²  + 9 (√3/2)² – 6 (2/√3)² – (9/4)(√3) ²

∴ L.H.S. = 4 x 3  + 9 (3/4) – 6 (4/3) – (9/4)(3)

∴ L.H.S. = 12  + 27/4 – 8 – 27/4 = 4 = R.H.S,

∴ 4 cot² 30° + 9 sin² 60° – 6 cosec² 60°  -(9/4) tan² 60° = 4 (Proved)

Example 09:

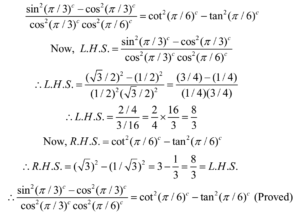
Example 10:

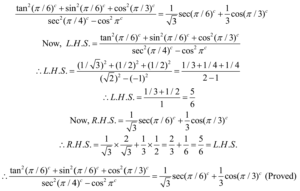
Example 11:

• If 2 cos²θ + 3cosθ = 2, then find cosθ.
• Solution:

Given 2 cos²θ + 3cosθ = 2  i.e 2 cos²θ + 3cosθ – 2 = 0

let cosθ = x

∴ 2 x² + 3x – 2 = 0

∴ 2 x² + 4x – x – 2 = 0

∴ 2 x(x + 2) – 1(x + 2) = 0

∴ (x + 2)(2x – 1) = 0

∴ (x + 2) = 0 or (2x – 1) = 0

∴ x = – 2 or x = 1/2

∴ cosθ = – 2 or cosθ = 1/2

Now – 1 ≤ cos θ ≤ 1, thus cosθ = – 2 is not possible.

∴ cosθ = 1/2\

Example 12:

• If 6sin²θ  – 11sinθ + 4 = 0, find cosθ.
• Solution:

Given 6sin²θ  – 11sinθ + 4 = 0

let sinθ = x

∴ 6x²  – 11x + 4 = 0

∴ 6x²  – 8x – 3x + 4 = 0

∴ 2x(3x  – 4) – 1(3x – 4) = 0

∴ (3x  – 4)(2x – 1) = 0

∴ 3x  – 4 = 0 or 2x – 1 = 0

∴ x = 4/3 or x = 1/2

Now – 1 ≤ sin θ ≤ 1, thus sinθ = 4/3 is not possible.

∴ sinθ = 1/2

Example 13:

• If 3tan²θ  – 4√3 tanθ + 3 = 0, then find tanθ.
• Solution:

Given 3tan²θ  – 4√3 tanθ + 3 = 0

let tanθ = x

∴ 3x²  – 4√3 x + 3 = 0

∴ 3x²  – 3√3 x –√3 x + 3 = 0

∴ √3 x √3 x²  – 3√3 x –√3 x + 3= 0

∴ √3 x ( √3x – 3 )  – 1(√3 x – 3) = 0

∴  (√3x – 3 )( √3 x – 1) = 0

 ∴ √3x – 3  = 0 or √3 x – 1 = 0

∴ x = 3/√3 or x = 1/√3

∴ x = √3 or x = 1/√3

∴  tanθ = √3 or tanθ = 1/√3

Example 14:

• If 4sin²θ  – 2(√3 + 1)sinθ + √3 = 0, then find sinθ. Hence find the angle θ.
• Solution:

Given 4sin²θ  – 2(√3 + 1)sinθ + √3 = 0

let sinθ = x

∴ 4x²  – 2(√3 + 1)x + √3 = 0

∴ 4x²  – 2√3x – 2x + √3 = 0

∴ 2x(2x  – √3) – 1(2x – √3 ) = 0

∴ (2x  – √3)(2x – 1) = 0

∴ 2x  – √3  = 0 or 2x – 1 = 0

∴ x = √3/2 or x = 1/2

∴  sinθ = √3/2 or sinθ = 1/2

∴ θ = sin^-1(√3/2) or θ = sin^-1(1/2)

∴ θ = (π/3)^c i.e. 60° or θ = (π/6)^c i.e. 30°

Example 15:

• Find the acute angles A and B satisfying cot (A + B) = 1 and cosec (A- B) = 2
• Solution:

Given cot (A + B) = 1 and cosec (A- B) = 2

we know that cot 45° = 1 and cosec 30° = 2

∴ A + B = 45° and A- B = 30°

Adding the two equations we get

2A = 75° i.e. A = 37.5°

Subtracting the two equations we get

2B = 15° i.e. B = 7.5°

∴ A = 37.5° and B = 7.5°

Example 16:

• Find the acute angles secA.cotB – secA – 2 cotB + 2 = 0
• Solution:

Given secA.cotB – secA – 2 cotB + 2 = 0

secA.(cotB – 1) – 2 (cotB – 1) = 0

(cotB – 1)(secA – 2) = 0

∴ cotB – 1 = 0  and/or secA – 2 = 0

∴ cotB = 1 and/or secA = 2

∴B =  cot^-11 and/or A = sec^-12

∴B = (π/4)^c i.e. 45° and/or A = (π/3)^c i.e. 60°

∴ A = (π/3)^c i.e. 60° and B = (π/4)^c i.e. 45°