Science > Physics > Circular Motion > Numerical Problems on Banking of Road
Example – 01:
To what angle must a racing track of radius of curvature 600 m be banked so as to be suitable for a maximum speed of 180 km/h?
Given: maximum speed v = 180 km/hr = 180 x 5/18 = 50 m/s, Radius of curvature = r = 600 m, g = 9.8 m/s2
To Find: Angle of banking = θ =?
Solution:
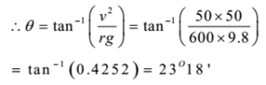
Ans: Angle of banking = 23° 18’
Example – 02:
A curve in the road is in the form of an arc of a circle of radius 400 m. At what angle should the surface of the road be laid inclined to the horizontal so that the resultant reaction of the surface acting on a car running at 120 km/h is normal to the surface of the road?
Given: speed of the car = v = 120 km/hr = 120 x 5/18 = 33.33 m/s, radius of curve = r = 400m, g = 9.8 m/s2
To Find: Angle of banking = θ = ?
Solution:
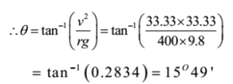
Ans: Angle of banking = 15° 49’
Example – 03:
A train of mass 105 kg rounds a curve of radius 150 m at a speed of 20m/s. Find the horizontal thrust on the outer rail if the track is not banked. At what angle must the track be banked in order that there is no thrust on the rail? g= 9.8 m/s2.
Given: mass of train = m = 105 kg, velocity of train = v = 20 m/s, radius of curve = r = 400m, g = 9.8 m/s2
To Find: Horizontal thrust = F =? Angle of banking = θ = ?
Solution:
The horizontal thrust is equal to the centripetal force in magnitude.

Ans: Horizontal thrust = 2.67 x 105 N, the angle of banking = 15° 13’
Example – 04:
The radius of curvature of a metre gauge railway line at a place where the train is moving at 36 km/h is 50m. If there is no side thrust on the rails find the elevation of the outer rail above the inner rail.
Given: speed of train = v = 36 km/hr = 36 x 5/18 = 10 m/s, radius of curve = r = 50m, g = 9.8 m/s2, For metre gauge, distance between rail = l = 1 m.
To Find: elevation = h =?
Solution:

Ans: The elevation of outer rail over inner rail = 0.2 m
Example – 05:
Find the angle of banking of the railway track of radius of curvature 3200 m if there is no side thrust on the rails for a train running at 144 km/h. Find the elevation of the outer rail above the inner one if the distance between the rails is 1.6 m.
Given: Speed of train = v = 144 km/hr = 144 x 5/18 = 40 m/s, radius of curve = r = 3200m, g = 9.8 m/s2, distance between rail = l = 1.6 m.
To find: Angle of banking = θ =? Elevation = h =?
Solution:

Ans: The angle of banking = 2°55’, the elevation of outer rail over inner rail = 81 mm
Example – 06:
A metre gauge train is moving at 60 km/hr along a curved rod of a radius of curvature 500m at a certain place. Find the elevation of outer rail over the inner rail, so that there is no side pressure on the rail. (g = 9.8 m/s2)
Given: Speed of train = 60 kmph = 60 x 5/18 =16.67 m/s, radius of curve = r = 500 m, distance between rail = l = 1 m. g = 9.8 m/s2
To find: elevation of outer rail over the inner rail = h =?
Solution:
The angle of banking is given by

Elevation h = l sinθ = 1 x sin (3o15’) = 1x 0.0567 =0.0567 m = 5.67 cm
Ans: The angle of banking is 3o15’ and the elevation of outer rail over the inner rail is 5.67 cm
Example – 07:
A vehicle enters a circular bend of radius 200 m at 72 km/h. The road surface at the bend is banked at 10°. Is it safe? At what angle should the road surface be ideally banked for safe driving at this speed? If the road is 5m wide, what should be the elevation of the outer edge of the road surface above the inner edge?
Given: Speed of vehicle = v = 72 km/hr = 72 x 5/18 = 20 m/s, Angle of banking = θ = 10°, radius of curve = r = 200 m, g = 9.8 m/s2
To Find: Part – I: To check safety, part – II: nagle of banking = θ =? for given speed, elevation = h =?
Solution:
Part – I:

Now, the velocity of the vehicle (20 m/s) is greater than the safe velocity (18.59 m/s). Hence it is unsafe to drive at a speed 72 km/hr.
Part – II:

Ans: It is unsafe to drive at the speed 72 km/hr. The angle of banking for speed 72 km/hr = 11°32’, Elevation of the outer edge over inner edge = 1m
Example – 07:
Find the minimum radius of an arc of a circle that can be negotiated by a motorcycle, riding at 21 m/s if the coefficient of friction between the tyres and the ground is 0.3. What is the angle made with the vertical by the motorcyclist? g = 9.8 m/s2.
Given: Velocity of motor cycle = v = 21 m/s, Coefficient of friction = μ = 0.3, g = 9.8 m/s2
To Find: radius of curvature = r =?, Angle with vertical = θ= ?
Solution:
Necessary centripetal force is provided by the friction between the road and tyres.

Ans: Radius of the circular path = 150 m, Angle made by the motorcyclist with vertical = 16°42’
Example – 08:
What is the angle of banking necessary for a curved road of 50 m radius for safe driving at 54 km/h? If the road is not banked, what is the coefficient of friction necessary between the road surface and tyres for safe driving at this speed?
Given: velocity of vehicle = v = 54 km/hr = 54 x 5/18 = 15 m/s, radius of curve = r = 50m, g = 9.8 m/s2
To Find: Angle of banking = θ =? coefficient of friction = μ = ?
Solution:

When the road is not banked, the necessary centripetal force is provided by the friction between the road and tyres.

Ans: The angle of banking = 24°42’, the coefficient of friction = 0.4592
Example – 09:
A motorcyclist at a speed of 5 m/s is describing a circle of radius 25 m. Find his inclination with the vertical. What is the value of the coefficient of friction between the road and tyres?
Given: Speed of motor cycle = v = 5 m/s, radius of circle = r = 25 m, g = 9.8 m/s2,
To find: Angle of inclination = θ=? Coefficient of friction = μ = ?
Solution:

Necessary centripetal force is provided by the friction between the road and tyres.

Ans: Angle made with the vertical = 5°49’, The coefficient of friction = 0.1020
Example – 10:
A motor van weighing 4400 kg rounds a level curve of radius 200 m on the unbanked road at 60 km/hr. What should be the minimum value of the coefficient of friction to prevent skidding? At what angle the road should be banked for this velocity?
Given: Mass of vehicle = m = 4400 kg, velocity of vehicle = v = 60 km/hr = 60 x 5/18 = 16.67 m/s, r = 200m, g = 9.8 m/s2
To Find: Coefficient of friction = μ =?, Angle of banking = θ = ?,
Solution:
Necessary centripetal force is provided by the friction between the road and tyres.

Ans: The coefficient of friction = 0.1418, The angle of banking = 8°4’
Example – 11:
A circular road course track has a radius of 500 m and is banked to 10°. If the coefficient of friction between the road and tyre is 0.25. Compute (i) the maximum speed to avoid slipping (ii) optimum speed to avoid wear and tear of the tyres.
Solution:
Given: radius of curve = r = 500m, Angle of banking = θ = 10°, coefficient of friction = μ = 0.25, g = 9.8 m/s2,
To find: safe velocity = v =? to avoid wear and tear v = ?
Maximum sped to avoid slipping.

Maximum speed to avoid wear and tear

Ans: The maximum velocity to avoid skidding = 46.74 m/s, The maximum velocity to avoid wear and tear of tyres. = 29.39 m/s.
Example – 06:
An aircraft in level flight completes a circular turn in 100 seconds. What is the radius of the circular turn? What is the angle of banking, if the velocity of aircraft is 40 m/s?
Given: Time taken = T = 100 s. velocity of aircraft = 40 m/s.
To Find: radius of circular turn = ?, angle of banking = θ = ?
Solution:
100 seconds are taken to complete a circular turn (circumference)

Ans: The angle of banking of aircraft is 14°25′
Previous Topic: Theory of Banking of Road
Next Topic: Concept of Conical Pendulum

One reply on “Numerical Problems on Banking of Road”
Thank you so much this was really helpful