Science > Physics > Wave Theory of Light > Numerical Problems on wave Theory of Light
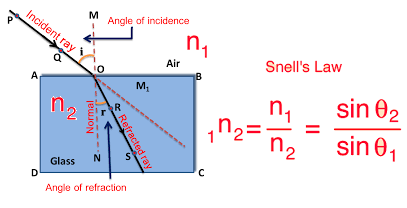
In this article, we shall study to solve the problems on the calculation of the refractive index, angle of refraction, the wavelength of light and wavenumber of waves using snell’s law and the definition of the refractive index of the medium.
Example 01:
A ray of light is incident on a glass slab making an angle of 25° with the surface. Calculate the angle of refraction in glass and velocity of light in the glass, if the refractive index of glass and velocity of light are 1.5 and 3 x 108 m/s respectively.
Given: Glancing angle = ig = 25o, Refractive index = μ = 1.5, Velocity of light in air = ca = 3 x 108 m/s
To Find: Angle of refraction = r =? Velocity of light in glass = cg = ?
Solution:
Angle of incidence = 90o – glancing angle = 90o – 25o = 65o.
μ = sin i / sinr
∴ sin r = sin i / μ = sin 65o / 1.5 = 0.9063/1.5 = 0.6042
∴ r = sin-1 (0.6042)
∴ Angle of refraction = 37o10’
Now, μ = ca/cg
∴ cg = ca/ μ = 3 x 108 /1.5 = 2 x 108 m/s
Ans: Angle of refraction = 37O10’ and velocity of light in glass = 2 x 108 m/s
Example 02:
A ray of light is incident on a glass slab making an angle of 60o with the surface. Calculate the angle of refraction in glass and the velocity of light in glass if the refractive index of glass and the velocity of light in air 1.5 and 3 x 108 m/s respectively.
Given: Glancing angle = ig = 60o, Refractive index = μ = 1.5, Velocity of light in air = ca = 3 x 108 m/s
To Find: Angle of refraction = r =? Velocity of light in glass = cg = ?
Solution:
Angle of incidence = 90o – glancing angle = 90o – 60o = 30o.
μ = sin i / sinr
∴ sin r = sin i / μ = sin 30o / 1.5 = 0.5/1.5 = 0.3333
∴ r = sin-1 (0.3333)
∴ Angle of refraction = 19o28’
Now, μ = ca/cg
∴ cg = ca/ μ = 3 x 108 /1.5 = 2 x 108 m/s
Ans: Angle of refraction = 19O28’ and velocity of light in glass = 2 x 108 m/s
Example 03:
A plane wavefront is made incident at an angle of 30° on the surface of the glass. Calculate angle of refraction if R.I. of glass is 1.5. Also find angle of deviation.
Given: Angle of incidence = i = 30o, Refractive index = μ = 1.5,
To Find: Angle of refraction = r =? Angle of deviation = δ =?
Solution:
μ = sin i / sinr
∴ sin r = sin i / μ = sin 30o / 1.5 = 0.5/1.5 = 0.3333
∴ r = sin-1 (0.3333)
∴ Angle of refraction = 19o28’
δ = i – r = 30o – 19o28’ = 10o32’
Ans: Angle of refraction = 19O28’ and angle of deviation = 10o32’
Example 04:
The wave number of beam of light in air is 2.5 x 106 per metre. What is the wavelength in glass if R.I. of the glass is 1.5?
Given: Wave number in air = 2.5 x 106 per metre, Refractive index = μg = 1.5,
To Find: Wavelength in glass = λg =?
Solution:
Wave length in air = λa = 1/Wave number in air = 1/ 2.5 x 106 = 4 x 10-7 m
μg = λa / λg
∴ λg = λa / μg = 4 x 10-7 / 1.5 = 2.667 x 10-7 m
∴ λg = 2.667 x 10-7 x 1010 = 2667 Å
Ans: Wavelength of light in glass is 2667 Å
Example 05:
What is the wave number of a beam of light in air if its frequency is 14 x 1014Hz? c = 3 x 108 m/s.
Given: Frequency in air = νa = 14 x 1014 Hz, Velocity of light in air = ca = 3 x 108 m/s
To Find: Wave number in air =?
Solution:
We have = ca = νa λa
1/λa = νa /ca = 14 x 1014 / 3 x 108 = 4.67 x 106 m-1
∴ Wave number = 1/λa = 4.67 x 106 m-1
Ans: Wave number in air is 4.67 x 106 m-1
Example 06:
The wavelength of monochromatic light is 5000 A.U. What will be its wave number in a medium of R.I. 1.5?
Given: Wavelength in air = λa = 5000 Å = 5000 x 10-10 m = 5 x 10-7 m, Refractive index of medium = 1.5
To Find: Wave number in medium =?
Solution:
μm = λa / λm
1/λm = μm /λa = 1.5/ 5 x 10-7 = 3 x 106 m-1
∴ Wave number in medium = 1/λm = 3 x 106 m-1
Ans: Wave number in medium is 3 x 106 m-1
Example 07:
The wavelength of a beam of light in glass is 4400 Å. What is its wavelength in air, if refractive index of glass is 1.5?
Given: Wavelength in glass = λg = 4400 Å, Refractive index of medium = 1.5
To Find: Wavelength in air = λa =?
Solution:
μg = λa / λg
∴ λa = μg λg = 1.5 x 4400 = 6600 Å
Ans: Wavelength in air is 6600 Å
Example 08:
The speed of light in air is 3 x 108 m/s and that in diamond is 1.4 x 108 m/s. Find the R.I. of diamond.
Given: Speed of light in air = ca = 3 x 108 m/s, Speed of light in diamond = cd = 1.4 x 108 m/s, Refractive index of medium = 1.5
To Find: Refractive index of diamond = μd =?
Solution:
μd = ca / cd = 3 x 108 / 1.4 x 108 = 2.142
Ans: Refractive index of diamond is 2.142
Example 09:
The velocity of light in diamond is 1.25 x 108 m/s. Find the refractive index of diamond w.r.t. water. R.I. of water w.r.t. air is 1.33. Speed of light in air is 3 x 108 m/s
Given: Speed of light in diamond = cd = 1.25 x 108 m/s, Speed of light in air = ca = 3 x 108 m/s, R.I. of water = μw = 1.33
To Find: Refractive index of diamond w.r.t. water = wμd =?
Solution:
Refractive index of water w.r.t. air is given by
μw = ca / cw
cw = ca / μw = 3 x 108 /1.33 = 2.25 x 108 m/s
Refractive index of diamond w.r.t. water is given by
wμd = cw / cd = 2.25 x 108 /1.25 x 108 = 1.8
Ans: Refractive index of diamond w.r.t. water is 1.8
Example 10:
The refractive indices of glycerine and diamond with respect to air are 1.4 and 2.4 respectively. Calculate the speed of light in glycerine and in diamond. From these results calculate the refractive index of diamond w.r.t. glycerine. c= 3 x 108 m/s,
Given: Refractive index for glycerine = μg = 1.4, Refractive index for diamond = μd = 2.4, Speed of light in air = ca = 3 x 108 m/s, R.I. of water = μw = 1.33
To Find: Speed of light in glycerine = cg =? The speedof light in diamond = cd =?, Refractive index of diamond w.r.t. glycerine = gμd = ?
Solution:
Refractive index of glycerine w.r.t. air is given by
μg = ca / cg
cg = ca / μg = 3 x 108 /1.4 = 2.143 x 108 m/s
Refractive index of diamond w.r.t. air is given by
μd = ca / cd
cd = ca / μd = 3 x 108 /2.4 = 1.25 x 108 m/s
Refractive index of diamond w.r.t. glycerine is given by
gμd = cg / cd = 2.143 x 108 /1.25 x 108 = 1.71
Ans: Speed of light in glycerine is 2.143 x 108 m/s and that in diamond is 1.25 x 108 m/s, Refractive index of diamond w.r.t. glycerine is 1.71
Example – 11:
The refractive indices of water and diamond with respect to air are 4/3 and 2.42 respectively. Calculate the speed of light in water and in diamond. From these results calculate the refractive index of diamond w.r.t. water. c= 3 x 108 m/s,
Given: Refractive index for water = μw = 4/3 = 1.33, Refractive index for diamond = μd = 2.4, Speed of light in air = ca = 3 x 108 m/s,
To Find: Speed of light in water = cw =? The speed of light in diamond = cd =?, Refractive index of diamond w.r.t. water = wμd = ?
Solution:
Refractive index of water w.r.t. air is given by
μw = ca / cw
cw = ca / μw = 3 x 108 /1.33 = 2.25 x 108 m/s
Refractive index of diamond w.r.t. air is given by
μd = ca / cd
cd = ca / μd = 3 x 108 /2.42 = 1.24 x 108 m/s
Refractive index of diamond w.r.t. water is given by
wμd = cw / cd = 2.25 x 108 /1.24 x 108 = 1.815
Ans: Speed of light in water is 2.25 x 108 m/s and that in diamond is 1.25 x 108 m/s and Refractive index of diamond w.r.t. water is 1.815
Example 12:
The wavelength of light in water is 4000 Å and in the glass is 2500 Å Find the refractive index of glass w.r.t. water.
Given: SWavelength in water = λw = 4000 Å, Wavelength in glass = λg = 2500 Å
To Find: Refractive index of glass w.r.t. water = wμg = ?
Solution:
μw = λw / λg = 4000 / 2500= 1.6
Ans: Refractive index of glass w.r.t. water is 1.6
Example 13:
The refractive indices of two media are 1.5 and 1.7. Calculate the velocity of light in these two media.
Given: Refractive index of first medium = μ1 = 1.5, Refractive index of second medium = μ2 = 1.7, Speed of light in air = ca = 3 x 108 m/s,
To Find: Velocity of light in the two media = c1 =? c2 =?
Solution:
Consider first medium, μ1 = ca / c1
c1 = ca / μ1 = 3 x 108 /1.5 = 2 x 108 m/s
Consider second medium, μ2 = ca / c2
c2 = ca / μ2 = 3 x 108 /1.7 = 1.76 x 108 m/s
Ans: Velocity of light in first medium is 2 x 108 m/s and in second medium is 1.76 x 108 m/s
Example 14:
Red light of wavelength 6400 Å. in air has a wavelength of 4000 Å in glass. If the wavelength of the violet light in air is 4400 Å. What is its wavelength in glass?
Given: Wavelength in air for red light = λar = 6400 Å, Wavelength in glass for red light = λgr = 4000 Å, Wavelength in air for violet light = λav = 4400 Å,
To Find: Wavelength in glass for violet light = λgv =?
Solution:
Consider red light
μr = λar / λgr = 6400 /4000= 1.6
Assuming the refractive index for both colour is same i.e. μr = μv
Consider violet light
μv = λav / λgv
λgv= λav / μv = 4400/1.6 = 2750 Å
Ans: Wavelength of violet colour in glass is 2750 Å
Example 15:
A beam of red light (7000 Å) is passing from air into a medium making an angle of incidence of 61° and angle of refraction of 34°. Find the wavelength of red light in the medium.
Given: Wavelength of red light in air = λa = 7000 Å,Angle of incidence = i = 61°, Angle of refraction = r = 34°,
To Find: Wavelength of red light in medium = λm =?
Solution:
Refractive index of medium
μ = sin i / sinr = sin 61° / sin34° = 0.8746 / 0.5592= 1.564
Consider first medium, μm = λa / λm
λm = λa / μm = 7000/1.564 = 4476 Å
Ans: wavelength of red light in the medium is 4476 Å.
Previous Topic: Applications of wave Theory of Light
Next Topic: More Problems on Wave Theory of Light