Science > Physics > Communication > Coverage Area of Antenna
An antenna or aerial is a system of elevated conductors which couples the transmitter or receiver to the communication channel. Thus it is required at both ends i.e. transmitter end and receiver end. The same antenna can be used for transmitting and receiving functions.
Expression for Coverage Area of Transmission Antenna:
Let us consider a TV transmission antenna ST of height ‘h’ situated at point S on the surface of the earth. Let O be the centre of the earth and Re be the radius of the earth. Let P be the point on the surface of the earth at a distance of ‘d’ from S beyond which the signal emitted from transmitter T cannot be received. TP is tangent to the earth’s surface. The height of the tower is negligible compared to range. Hence SP = PT = d
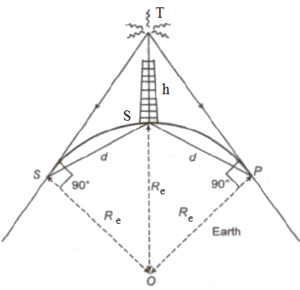
Δ OPT is right angled triangle. By Pythagoras theorem
OT2 = OP2 + PT2
∴ (Re + h)2 = Re2 + d2
∴ Re2 +2 Reh + h2 = Re2 + d2
∴ d2 = 2 Reh + h2
Now h is small compared to the radius of the earth. Hence h2 can be neglected.
∴ d2 = 2 Reh
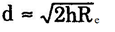
Using the formula A = πd2, the coverage area is calculated
Using the formula Population covered = A x population density of that area, the viewership is calculated.
Numerical Problems:
Example – 1:
A TV tower has a height of 100 m. What is the maximum distance up to which the TV transmission can be received? The radius of the earth is 6400 km. If the population density of the region is 500 per square kilometre, find the population reach of the transmission.
Given: Height of tower = h = 100 m, Radius of earth = R = 6400 km = 6.4 x 106 m, Population density = 500 per square kilometre
To Find: Maximum range = d =? Population reach =?
Solution:

D = 35.77 km
Area of reach A = pd2 = 3.142 x (35.77)2 = 4020 square kilometer
Population reach = Area of reach x population density
Population reach = 4020 x 500 = 2.01 x 106 or 2.01 million
Ans: Coverage range = 35.77 km, Population reach = 2.01 million
Example – 2:
A TV tower has a height of 160 m. What is the maximum distance up to which the TV transmission can be received? The radius of the earth is 6400 km. If the population density of the region is 1200 per square kilometre, find the population reach of the transmission.
Given: Height of tower = h = 160 m, Radius of earth = R = 6400 km = 6.4 x 106 m, Population density = 500 per square kilometre
To Find: Maximum range = d =? Population reach =?
Solution:

D = 45.25 km
Area of reach A = pd2 = 3.142 x (45.25)2 = 6430 square kilometer
Population reach = Area of reach x population density
Population reach = 6430 x 1200 = 7.72 x 106 or 7.72 million
Ans: Coverage range = 45.25 km, Population reach = 7.72 million
Example – 3:
A TV tower has a height of 160 m. What should be the increase in the height of the tower so that the coverage range is doubled? Also, find percentage increase in the height of the tower.
Given: Height of tower = h1 = 160 m, d2 = 2d1.
To Find: Increase in height of tower = h2 – h1 =?, % increase in height =?
Solution:

h2 = 4 x 160 = 640 m
The increase in height of tower = 640 m – 160 m = 480 m

Ans: The increase in height of the tower is 480 m and % increase is 300 %
Example – 4:
If a height of a transmitting tower is increased by 21%. By what percentage the range of the tower is affected.
Given: % change in height of tower = 21%
To Find: Percentage change in the range of tower =?
Solution:
% increase in the height of the tower
h2 = h1 + 21% h1 = h1 + 0.21 h1 = 1.21 h1

Ans: Percentage increase in coverage range is 10%
Example – 5:
A transmitting antenna at the top of the tower has a height of 50 m and that on receiving antenna is 32 m. What is the maximum possible distance between them for satisfactory communication in the line of sight mode? The radius of the earth is 6400 km.
Given: Height of transmitting tower = hT 50 m = 0.050 km, Height of receiving tower = hR 32 m = 0.032 km, Radius of earth = R = 6400 km
To Find: Maximum distance between the tower =?
Solution:

Ans: Maximum distance between towers is 45.53 km
Example – 6:
A fax message is to be sent from Delhi to Washington using a geostationary satellite, If the height of geostationary height above the surface of the earth is 36000 km, find the time delay between the dispatch and being received. The radius of the Earth is 6400 km.
Solution:
Given: Height of satellite above the surface of the earth = h = 36000 km, Radius of earth = R = 6400 km
To Find: time delay between the dispatch and being received =?
Assuming the maximum range = distance between the two cities

The motion of the electromagnetic wave is a uniform motion
Thus time delay = d/c = 21500 x 103 / 3 x 108 =7.17 x 10-2 s
Ans: Thus the time delay between the dispatch and being received is 7.17 x 10-2 s
Example – 7:
A radar has a power of 1kW is operating at a frequency 10 GHz is located at a mountaintop of 500 m. Find the maximum distance up to which it can detect an object located on the surface of the earth. The radius of the earth is 6400 km.
Solution:
Given: height of the radar above the surface = h = 500 m = 0.5 km, Radius of earth = R = 6400 km
To Find: Maximum distance of reach = d = ?
The height h is negligible w.r.t. the radius of the earth

Ans: The maximum distance up to which it can detect an object is 80 km
Maximum Line of Sight Distance:
At the frequency of 40 MHz, the communication is limited to line of sight paths. At these frequencies the size of the antenna is relatively smaller than the radius of the earth, the curvature of the earth blocks the direct transmission of the wave from transmitter t the receiver. Let C be such a point. Let T be the position of transmitting antenna and R be the position of the receiving antenna. Let hT be the height of the transmitting antenna and hR be the height of receiving antenna. Let dT be the maximum range of transmitting antenna and dR be the maximum range of receiving antenna. Now AB is tangent to the earth’s surface at C. AB is the maximum line of sight distance

AB = dT + dRT

Previous Topic: Communication Channel: The Atmosphere
Next Topic: Satellite Communication