Applications of Parallel and Perpendicular Axes Theorems

Science > Physics > Rotational Motion > Applications of Parallel and Perpendicular Axes Theorems

The parallel axes theorem states that ” The moment of inertia of a rigid body about any axis is equal to the sum of its moment of inertia about a parallel axis through its centre of mass and the product of the mass of the body and the square of the distance between the two axes.”

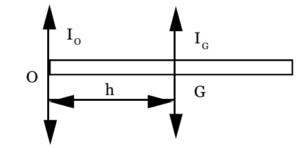
I_O = I_G +  Mh²

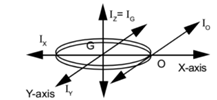
The perpendicular axes theorem states that ” Moment of inertia of a rigid plane lamina about an axis perpendicular to its plane is equal to the sum of its moment of inertia about any two mutually perpendicular axes in its plane and meeting in the point where the perpendicular axis cuts the lamina.”

l_z    =    l_x  +   l_y

Expression for Moment of Inertia of a Uniform Rod About a Transverse Axis Passing Through its End:

 We know that  moment of inertia of a thin  rod about a transverse axis passing through its centre G is given  by

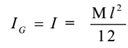
We have to find the Moment of Inertia about the parallel transverse axis passing through the end of the rod.  Let I_o be the moment of Inertia about this axis. Then by the principle of parallel axes,

This is an expression for moment of inertia of a thin uniform rod about a transverse axis passing through its end.

Expression for Moment of Inertia  of Thin Uniform Disc About its Tangent Perpendicular to its Plane:

The moment of inertia of thin uniform disc about a transverse axis passing through its centre is given by

We have to find the M.I. about a tangent perpendicular to the plane of the disc. These two axes are parallel to each other. By parallel axes theorem,

This is an expression for M.I. of a thin uniform disc about its tangent perpendicular to its plane.

Expression for Moment of Inertia of Thin Uniform Ring About its Tangent Perpendicular to its Plane:

The moment of inertia of thin uniform ring about a transverse axis passing through its centre is given by

I = MR² = I_G

We have to find the M.I. about a tangent perpendicular to the plane of the ring. These two axes are parallel to each other. By parallel axes theorem

I_O =  I_G +  Mh²

∴   I_O =  MR² +  MR²

∴   I_O =  2 MR²

This is an expression for M.I. of a thin uniform ring about its tangent perpendicular to its plane.

Expression for Moment of Inertia of Thin Uniform Disc About its  Diameter:

The moment of inertia of thin uniform disc about a transverse axis passing through its centre is given by

We have to find the M.I. about a diameter of the disc. Let us consider a system of three axes, such that the z-axis is along the geometrical axis of the disc and x-axis and y-axis lie in the plane of the disc such that the centre of mass G lies at the origin of the system of axes.

By perpendicular axes theorem, we have

l_z    =    l_x  +   l_y   …………. (2)

Due to symmetry M.I. of the disc about diameter is

l_d  =  l_x  =   l_y   …………. (3)

Substituting values of equations (1) and (3) in (2)

This is an expression for M.I. of a thin uniform disc about its diameter.

Expression for Moment of Inertia  of Thin Uniform Ring About its  Diameter:

The moment of inertia of thin uniform ring about a transverse axis passing through its centre is given by

I = MR²

We have to find the M.I. about a diameter of the ring. Let us consider a system of three axes, such that the z-axis is along the geometrical axis of the ring and x-axis and y-axis lie in the plane of the ring such that the centre of mass G lies at the origin of the system of axes.

l_z  = MR²  ………(1)

By perpendicular axes theorem, we have

l_z    =    l_x  +   l_y   …………. (2)

Due to symmetry M.I. of the disc about diameter is

l_d  =  l_x  =   l_y   …………. (3)

Substituting values of equations (1) and (3) in (2)

This is an expression for M.I. of a thin uniform ring about its diameter.

Expression for Moment of Inertia of a Thin Uniform Disc About an Axis Tangent to the Disc and in the Plane of the Disc:

The moment of inertia of thin uniform disc about a transverse axis passing through its centre is given by

We have to find the M.I. about a diameter the disc first. Let us consider a system of three axes, such that the z-axis is along the geometrical axis of the disc and x-axis and y-axis lie in the plane of the disc such that the centre of mass G lies at the origin of the system of axes.

By perpendicular axes theorem, we have

l_z    =    l_x  +   l_y   …………. (2)

Due to symmetry M.I. of the disc about diameter is

l_d  =  l_x  =   l_y   …………. (3)

Substituting values of equations (1) and (3) in (2)

Now y axis passes through the centre of mass G of the disc

Now the tangent to the disc in the plane of the disc is parallel to the y-axis.

By parallel axes theorem.

This is an expression for M.I. of a thin uniform disc about its tangent in its plane and in the plane of the disc.

Expression for Moment of Inertia of a Thin Uniform Ring About an Axis Tangent to the Ring and in the Plane of the Ring:

The moment of inertia of thin uniform ring about a transverse axis passing through its centre is given by

l = MR²

We have to find the M.I. about a diameter the ring first. Let us consider a system of three axes, such that the z-axis is along the geometrical axis of the ring and x-axis and y-axis lie in the plane of the ring such that the centre of mass G lies at the origin of the system of axes.

l_z  = MR²  ………(1)

By perpendicular axes theorem, we have

l_z    =    l_x  +   l_y   …………. (2)

Due to symmetry M.I. of the disc about diameter is

l_d  =  l_x  =   l_y   …………. (3)

Substituting values of equations (1) and (3) in (2)

Now the tangent to the ring in the plane of the ring is parallel to the y-axis.

By parallel axes theorem.

This is an expression for M.I. of a thin uniform ring about its tangent in its plane.

Expression for Moment of Inertia  of a Solid Cylinder About a Transverse Axis Passing Through its Centre:

Consider a solid cylinder of mass M, length ‘’ and radius ‘r’ capable of rotating about its geometrical axis. Let ‘m be its mass per unit length.

m = M/l      Hence M = m . l

A solid cylinder can be regarded as a number of thin uniform discs of infinitesimal thickness piled on top of one another. Let us consider one such disc of thickness ‘dx’ at a distance of ‘x’ from the centre C of the cylinder.

Mass of such disc is given by

Mass, dm = m.dx  = (M/l) dx

The M.I. of such disc about a transverse axis (passing through C) is given by

The M.I. of a disc about diameter is given by

Integrating above expression in limits

This is an expression for M. I. of a solid cylinder about a transverse axis passing through its centre.

Expression for Moment of Inertia of a Hollow Cylinder About a Transverse Axis Passing Through its Centre:

Consider a hollow cylinder of mass M, length ‘’ and radius ‘r’ capable of rotating about its geometrical axis. Let ‘m be its mass per unit length.

m = M/l      Hence M = m . l

A hollow cylinder can be regarded as a number of thin uniform rings of infinitesimal thickness piled on top of one another. Let us consider one such ring of thickness ‘dx’ at a distance of ‘x’ from the centre C of the cylinder.

Mass of such ring is given by

Mass, dm = m.dx  = (M/l) dx

The M.I. of such ring about a transverse axis (passing through C) is given by

dI = dm . R²

The M.I. of a ring about diameter is given by

Integrating the above expression in limits

This is an expression for M. I. of a hollow cylinder about a transverse axis passing through its centre.

Expression for Moment of Inertia of a Solid Sphere About its Tangent.

The moment of inertia of a solid sphere about its geometrical  axis (diameter) is given by

We have to find the M.I. about a tangent to the sphere. These two axes are parallel to each other. By parallel axes theorem

This is an expression for M.I. of a solid sphere

Previous Topic: Derivation of Expression for M.I.

Next Topic: Numerical Problems on Moment of Inertia

Science > Physics > Rotational Motion > Applications of Parallel and Perpendicular Axes Theorems