Science > Physics > Gravitation > Binding Energy of Satellite
In this article, we shall study the concept of the binding energy of satellite and its significance.
The binding energy of a satellite can be defined as the minimum amount of energy required to be supplied to it in order to free the satellite from the gravitational influence of the planet (i.e. in order to take satellite from the orbit to a point at infinity).
Binding energy gives us an idea about the energy by which the satellite is bound to the planet. This binding energy will be used to overcome the gravitational force of attraction between the Satellite and the planet.
Expression for Binding Energy of a Satellite Orbiting Around the Earth:
Consider a satellite revolving around the earth in a circular orbit. Necessary centripetal force to keep the satellite orbiting in a stable circular orbit is provided by the force of gravitational attraction between the earth and the satellite.
When the satellite is orbiting around the earth it possesses two types of mechanical energies. The kinetic energy due to its orbital motion and the potential energy due to its position in the gravitational field of the earth.
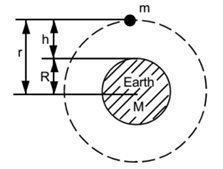
Let, M = the mass of the earth
R = the radius of the earth
h = the height of the satellite above the surface of the earth
vc = the critical velocity of the satellite
m = the mass of the satellite.
r = the radius of a circular orbit of the satellite = (R + h)
Kinetic Energy of satellite:
As the gravitational force is providing the necessary centripetal force required for circular motion,

Now, Centripetal force = Gravitational force
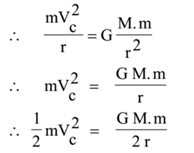
Where G is Universal gravitational constant.
The kinetic energy of a satellite orbiting around the earth is given by

Potential Energy:
Now, the satellite is in the gravitational field of the earth. The gravitational potential at a point on the surface of the earth is given by

The potential energy of a body (satellite) Is given by
P.E. = The gravitational potential x the mass of a satellite

Total Energy of Satellite:
The total mechanical energy of the satellite In orbit is given by
T.E. = K.E. + P.E.

The negative sign indicates that the satellite is bound to the earth by attractive forces and cannot leave it on its own. To move the satellite to infinity .we have to supply energy from outside the planet-satellite system. This energy is known as the binding energy of a satellite.
Binding Energy of Satellite:
B.E. = (Energy of a Satellite at Infinity) – (The energy of the satellite in the orbit)

This is an expression for Binding Energy of a satellite orbiting around the earth In stable circular orbit. Numerically, Binding Energy is equal to the total energy of a satellite in the orbit.
Expression for Binding Energy of a Satellite Stationary on the Earth’s Surface:
Consider a satellite of mass ‘m’ which is at rest on the earth’s surface. As the satellite is at rest, it will not possess any kinetic energy. i.e. K.E. = 0.
Now, the satellite is in the gravitational field of the earth. The gravitational potential at a point on the surface of the earth is given by

The potential energy of a body (satellite) Is given by
P.E. = The gravitational potential x the mass of a satellite

The total mechanical energy of the satellite on the surface of the earth is given by
T.E. = K.E. + P.E.

The negative sign indicates that the satellite is bound to the earth by attractive forces and cannot leave it on its own. To move the satellite to infinity we have to supply energy from outside the planet-satellite system. This energy is known as the binding energy of a satellite.
Binding Energy:
B.E. = (Energy of a Satellite at Infinity) – (The energy of the satellite in the orbit)

This is an expression for the binding energy of a satellite stationary on the earth’s surface.


Numerical Problems on Binding Energy:
Example – 01:
Two satellites A and B are moving in circular orbits of radii 3R and 5R respectively around the same planet. If the masses of satellites are in the ratio of 2:1, compute their critical velocities and binding energies and periods of revolution.
Given: radius orbit of satellite A = r1 = 3R, radius orbit of satellite B = r2 = 5R, Ratio of masses of satellite m1: m2 = 2 : 1
To find: ratio of critical velocities = v1 : v2 = ?, ratio of binding energies = B.E.1 : B.E.2 = ? , ratio of time periods = T1:T2 =?
Solution:


Ans: The ratio of critical velocities is √5: √3, The ratio of binding energy is 10 : 3, The ratio of periods is 0.465 : 1
Example – 02:
Calculate the work done in moving a body of mass 1000 kg from a height of 2R to a height 3R above the surface of the earth. Mass of the earth = 6 x 1024 kg; Radius of earth = 6400 km, G = 6.67 x 10-11 Nm2 /kg2.
Given: initial height = h1 = 2R, final height = h2 = 3R, mass of satellite = m = 1000 kg, Mass of earth = M = 6 x 1024 kg; radius of earth = R = 6400 km = 6.4 x 106 m, G = 6.67 x 10-11 Nm2 /kg2.
To Find: work done = W =?
Solution:
r1 = R + h1 = R + 2R = 3R,
r2 = R + h2 = R + 3R = 4R
Work done = Change in B.E.
Thus, W = B.E.1 – B.E.2

Ans: The work done is 2.615 x 109 J.
Example – 03:
What is the binding energy of a satellite of mass 2000 kg moving in a circular orbit around the earth close to its surface and at a height of 600 km? G = 6.67 x 10-11 S.I. units; Radius of earth = 6400 km; mass of earth = 6 x 1024 kg.
Given: mass of satellite = m = 2000 kg, G = 6.67 x 10-11 S.I. units; R = 6400 km = 6.4 x 106 m; Mass of earth = M = 6 x 1024 kg
To Find: Binding energies =?
Solution:
For satellite orbiting very close to earth’s surface h1 = 0
r1 = R + h1 = R + 0 = R

For second satellite h2 = 600 km
r1 = R + h1 = 6400 + 600 = 7000 km = = 7 x 106 m;

Ans: Binding energy of satellite orbiting very close to the earth’s surface is 6.25 x 1010 J and binding energy of satellite orbiting at height 600 km from the surface of the earth is 5.72 x 1010 J.
Example – 04:
What is the (i) KE (ii) PE (iii) total energy and (iv) binding energy of an artificial satellite of mass 100 kg orbiting at a height of 1600 km above the surface of the earth? Mass of the earth = 6 x 1024 kg; Radius of earth = 6400 km, G = 6.67 x 10-11 Nm2 /kg2.
Given: mass of satellite = m = 100 kg, Mass of earth = M = 6 x 1024 kg; radius of earth = R = 6400 km = 6.4 x 106 m, G = 6.67 x 10-11 Nm2 /kg2.
To Find: K.E. =? P.E. = ?, T.E. = ?, B.E. = ?,
Solution:
r = R + h = 6400 + 1600 = 8000 km = 8 x 106 m;

Binding energy = 2.5 x 109 J
Now total energy = – B.E. = – 2.5 x 109 J
Now potential energy = – 2 x B.E. = – 2 x 2.5 x 109 = – 5 x 109 J
Kinetic energy = B.E. = 2.5 x 109 J
Ans: The kinetic energy of satellite = 2.5 x 109 J, Potential energy of satellite = – 5 x 109 J, Total energy of satellite = – 2.5 x 109 J, Binding energy of satellite = 2.5 x 109 J
Example – 05:
Binding energy of a satellite is 4 x 108 J. Calculate its KE and PE.
Given: B.E = 4 x 108 J
To Find: K.E. =? P.E. = ?,
Solution:
Now Potential Energy = -2 x B.E. = -2 x 4 x 108 = – 8 x 108 J
Kinetic energy = B.E. = 4 x 108 J
Ans: Potential energy of satellite = – 8 x 108 J, the kinetic energy of satellite = 4 x 108 J
Example – 06:
What is the binding energy of a satellite of mass 80 kg moving in a circular orbit around the earth close to its surface and at a height of 1600 km? G = 6.67 x 10-11 S.I. units; Radius of earth = 6400 km; mass of earth = 6 x 1024 kg.
Given: mass of satellite = m = 80 kg, G = 6.67 x 10-11 S.I. units; R = 6400 km = 6.4 x 106 m; Mass of earth = M = 6 x 1024 kg; radius of earth = R = 6400 km = 6.4 x 106 m, G = 6.67 x 10-11 Nm2 /kg2.
To Find: B.E. =?
Solution:
For satellite orbiting very close to earth’s surface h1 = 0
r1 = R + h1 = R + 0 = R

For second satellite h2 = 1600 km
r1 = R + h1 = 6400 + 1600 = 8000 km = = 8 x 106 m;

Ans: The binding energy of satellite orbiting very close to the earth’s surface is 2.5 x 109 J and binding energy of satellite orbiting at height 600 km from the surface of the earth is 2 x 109 J.
Example – 06:
What is the (1) KE (2) PE (3) total energy and (4) binding energy of an artificial satellite of mass 1000 kg orbiting at a height of 3600 km above the surface of the earth? Mass of the earth = 6 x 1024 kg; Radius of earth = 6400 km, G= 6.67 x 10-11 Nm2 /kg2
Given: mass of satellite = m = 1000 kg, height of satellite above the surface of earth = 3600 km, Mass of earth = M = 6 x 1024 kg; radius of earth = R = 6400 km = 6.4 x 106 m, G = 6.67 x 10-11 Nm2 /kg2.
To Find: K.E. =? P.E. = ?, T.E. = ?, B.E. = ?,
Solution:
r = R + h = 6400 + 3600 = 10000 km = 104 m = 107 m;

Ans: Kinetic energy of satellite = 2 x 109 J, Potential energy of satellite = – 4 x 109 J, Total energy of satellite = – 2 x 109 J, Binding energy of satellite = 2 x 109 J
Example – 07:
What is the binding energy of an artificial satellite of mass 1000 kg orbiting a) at a height of 500 km above the surface of the earth and b) close to the earth’s surface? Mass of earth = M = 6 x 1024 kg; radius of earth = R = 6400 km = 6.4 x 106 m, G = 6.67 x 10-11 Nm2 /kg2.
Given: mass of satellite = 1000 kg, Mass of earth = M = 6 x 1024 kg; radius of earth = R = 6400 km = 6.4 x 106 m, G = 6.67 x 10-11 Nm2 /kg2.
To Find: B.E. =?
Solution:
For first case h1 = 5600 km
r1 = R + h1 = 6400 + 500 = 6900 km = = 6.9 x 106 m;

For satellite orbiting very close to erath’s surface h2 = 0
r2 = R + h2 = 6400 + 0 = 6400 km = = 6.4 x 106 m;

Ans: The binding energy of satellite orbiting at height 500 km from the surface of the earth is 2.9 x 1010 J and Binding energy of satellite orbiting very close to the earth’s surface is 3.127 x 1010 J
Example – 08:
A playful astronaut releases a bowling ball of mass 500 g into circular orbit about an altitude of 600 km. What is the mechanical energy of the ball in its orbit. radius of the earth = 6400 km, mass of earth = 6 x 1024 kg.
Given: mass of a ball = 500 g = 0.5 kg, height of satellite above the surface of the earth = 600 km, Radius of the earth = 6400 km, radius of orbit = 6400 + 600 = 7000 km = 7 x 106 m, mass of earth = 6 x 1024 kg.
To Find: Mechanical energy of ball = ET = ?
Solution:
B.E. = GMm/ 2r = ( 6.67 x 10-11 x 6 x 1024 x 0.5)/(2 x 7 x 106 )
B.E. = 1.43 x 107 J
Now total energy of satellite = T.E. = – B.E. = – 1.43 x 107 J
Ans: The mechanical energy of the ball in its orbit is – 1.43 x 107 J
Example – 09:
Find the binding energy of a body of mass 50 kg at rest on the surface of the earth. Given: G = 6.67 x 10-11 N m2/kg2, R = 6400 km = 6.4 x 106 m; M = 6 x 1024 kg.
Given: the mass of body = m = 50 kg, Universal gravitational constant = G = 6.67 x 10-11 N m2/kg2, R = 6400 km = 6.4 x 106 m; M = 6 x 1024 kg.
To find: binding energy of satellite = B.E. =?
Solution:
The binding energy of the body at rest on the surface of the earth is given by
B.E. = GMm/R = ( 6.67 x 10-11 x 6 x 1024 x 50)/(6.4 x 106 )
B.E. = 3.127 x 109 J
Ans: Binding energy of the body is 3.127 x 109 J
Previous Topic: Numerical Problems on Critical Velocity
One reply on “Binding Energy of Satellite”
Thanks for this article. It was very well written, explained from the basics and with the help of solved examples. Good work!