Science > Physics > Magnetic Effect of Electric Current > Biot-Savart’s Law
In this article, we shall study Biot-Savart’s Law and its application to find the magnetic induction at a point due to current carrying infinitely long conductor and the magnetic induction at the centre of a current-carrying circular coil.
Magnetic Induction:
The magnetic induction at any point in the magnetic field is defined as the magnetic flux passing through the unit area at that point. It is denoted by letter “B”. It is a vector quantity. Its S.I. unit is Wb/m² or tesla (T).
Mathematically, B = ∅ /A
Where B = Magnetic induction, ∅= Magnetic flux
A = Area through which magnetic flux is passing
Magnetic Induction Due to Current-Carrying Conductor:
Biot Savart’s law (Laplace’s Law):
The magnetic induction at a point near current-carrying conductor is directly proportional to (a) the current in the element (I), (b) the length of the element (dl), (c) the sine of the angle between the element and the straight line joining the element to the point, and inversely proportional to the square of the distance between the element and the point.
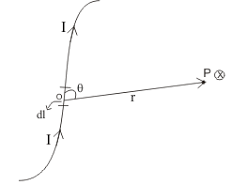
Explanation:
Consider a conductor of any shape in the form of wire. Let ‘i’ be the current through the conducting wire. Let ‘dl’ be a small element of the conductor, then the quantity i. dl is known as the current element of the conductor. Let P be the point at which magnetic induction due to current carrying conductor is to be found. Let be the position vector of point P with respect to the current element i.dl. Let θ be the angle between dl and r, then by Biot Savart’s law the magnetic induction due to the small element dl is given by
dB ∝ i …………….. (1)
dB ∝ dl ……………(2)
dB ∝ sinθ ……………(3)
dB ∝ 1/r² ……………(4)
From equations (1), (2), (3) and (4)
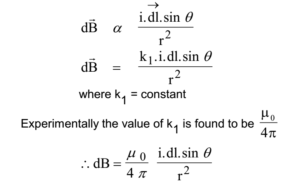
This is a mathematical expression for the Biot-Savart’s law.

This is a mathematical expression for the Biot-Savart’s law in the vector form.
The total magnetic induction due to current in the whole conductor is given by

Magnetic Induction at a Point Near an Infinitely Long Straight Current-Carrying Conductor:
Let us consider infinitely long straight conductor carrying current i. Let P be the point at which magnetic induction due to the current-carrying conductor is to be found. Let us consider a small element dl of the conductor at O. Let vector AP or vector r be the position vector of point P with respect to the current element. Let θ be the angle between the position vector of the point P and the current element. Let us draw PC perpendicular to the length of the conductor is drawn such that PC = R and OC = l. Now, angle COP = π – θ

Let dB be the magnetic induction at point ‘P’ due to the current-carrying conductor it is given by Biot Savart’s law.




This is an expression for magnetic induction at the point near the infinitely long straight conductor.
Magnetic Induction at Centre of Current-Carrying Circular Coil:
Consider a current-carrying coil having radius R and having a single turn. Let i be the current through this circular coil. Let O be the centre of the circular coil at which magnetic induction is to be found. Let dl be the small element of the current-carrying coil at P, let θ be the angle between the current element and line joining the current element with point O. In this case, θ = 900.

Magnetic induction at point O due to current element i. dl is given by Biot-Savart’s law

The total magnetic induction at “O” can be found by integrating both sides.

This is an expression for magnetic induction at the centre of the current-carrying circular coil.
Previous Topic: Magnetic Effect of Electric Current