Science > Physics > Interference of Light > Numerical Problems on Fringe Width
In this article, we shall study numerical problems based on Young’s experiment and biprism experiment to find the fringe width of the interference pattern and to find the wavelength of light used.
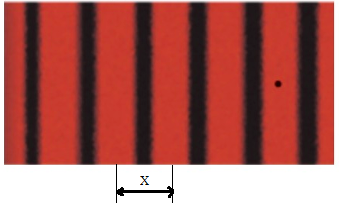
Example – 12:
In a biprism experiment, the slit is illuminated by the light of wavelength 5890 Å. The distance between the slit and the eye-piece is 0.8 m. The two virtual images of the slit are formed 0.2 cm apart. Calculate the change in fringe width if the eye-piece is displaced 10 cm away from the slit.
Solution:
Part – I:
Given: Distance between slits = d = 0.2 cm = 0.2 x 10-2 m = 2 x 10-3 m. Distance between slit and screen = D = 0.8 m, Wavelength of light = λ = 5890 Å = 5890 x 10-10 m = 5.89 x 10-7 m
To Find: Fringe width = X =?
The fringe width is given by X = λD/d
X = λD/d = (5.89 x 10-7 x 0.8)/( 2 x 10-3) = 2.356 x 10-4 m = 0.2356 mm
Part – II:
Given: For first case: fringe width = X1 = 0.2356 mm, distance of eye piece from the slits = D1 = 0.8 m, For second case: distance of eye piece from the slits = D2 = 0.8 m + 10 cm = 0.8 m + 0.1 m = 0.9 m
To Find: Change fringe width = ∆X =?
For first case X1 = λD1/d ………….. (1)
For second case, X2 = λD2/d ………….. (2)
Dividing equation (2) by (1)
X2 / X1 = (λD2/d) x (d/ λD1)
∴ X2 / X1 = D2/D1
∴ X2 = (D2/D1) x X1
∴ X2 = (0.9/0.8) x 0.2356 = 0.2651 mm
∴ Change in fringe width = ∆X = X2 – X1 = 0.2651 – 0.2356 = 0.0295 mm
Ans: The change in fringe width is 0.0295 mm
Example – 13:
In Young’s experiment the distance between two consecutive bright bands produced on a screen placed at 1.5 m from the two slits is 6.5 mm. What would be the fringe width if the screen is brought towards the slit by 50 cm for the same setting?
Given: For first case: fringe width = X1 = 6.5 mm, distance of screen from the slits = D1 = 1.5 m, For second case: distance of screen from the slits = D2 = 1.5 m – 50 cm = 1.5 m + 0.5 m = 1 m
To Find: New fringe width = X =?
Solution:
The fringe width is given by X = λD/d
For the first case X1 = λD1/d ………….. (1)
For the second case, X2 = λD2/d ………….. (2)
Dividing equation (2) by (1)
X2 / X1 = (λD2/d) x (d/ λD1)
X2 / X1 = D2/D1
X2 = (D2/D1) x X1
X2 = (1/1.5) x 6.5 = 4.33 mm
Ans: New fringe width is 4.33 mm
Example – 14:
In a biprism experiment, the fringe width is 0.4 mm when the eye-piece is at a distance of one metre from the slit. If now only the eye-piece is moved 25 cm towards the biprism, what would be the change in fringe width?
Given: For first case: fringe width = X1 = 0.4 mm, distance of eye piece from the slits = D1 = 1 m, for second case: distance of eye piece from the slits = D2 = 1 m – 25 cm = 1 m + 0.25 m = 0.75 m
To Find: Change fringe width = ∆X =?
Solution:
The fringe width is given by X = λD/d
For first case X1 = λD1/d ………….. (1)
For second case, X2 = λD2/d ………….. (2)
Dividing equation (2) by (1)
X2 / X1 = (λD2/d) x (d/ λD1)
X2 / X1 = D2/D1
X2 = (D2/D1) x X1
X2 = (0.75/1) x 0.4 = 0.3 mm
Change in fringe width = ∆X = X2 – X1 = 0.4 – 0.3 = 0.1 mm
Ans: There is decrease of 0.1 mm in fringe width
Example – 15:
In biprism experiment, light of wavelength 5200 Å is used to get an interference pattern on a screen. The fringe width changes by 1.3 mm when the screen is brought towards the biprism by 50 cm. Find the distance between the virtual images of the slit.
Given: Wavelength of light used = λ = 5200 Å = 5200 x 10-10 m = 5.2 x 10-7 m, change in fringe width = ΔX = 1.3 mm = 1.3 x 10-3 m, Initial distance of screen from virtual image = D1 = D m, final distance of screen from virtual image = D2 = D m – 50 cm = (D – 0.5) m
To Find: distance between the virtual images of the slit = d =?
Solution:
The fringe width is given by X = λD/d
For first case X1 = λD1/d ………….. (1)
For second case, X2 = λD2/d ………….. (2)
∆X = X1 – X2 = λD1/d – λD2/d = (λ/d)(D1 – D2) = (λ/d)(D – (D – 0.5)) =(λ/d)(0.5)
The change in fringe width = ∆X = (λ/2d)
d = (λ/2∆X) = (5.2 x 10-7) / (2 x1.3 x 10-3) = 2 x 10-4 m = 0.2 mm
Ans: The distance between the virtual images of the slit is 0.2 mm
Example- 16:
In biprism experiment, the separation of the slits is halved and the distance between the slits and the screen is doubled. How is the fringe width affected?
Given: Distance between slits d2 = ½ d1, Distance between screen and slit D2 = 2 D1
To Find: Change in fringe width = ∆X =?
Solution:
The fringe width is given by X = λD/d
For first case X1 = λD1/d1 ………….. (1)
For second case, X2 = λD2/d2 ………….. (2)
Dividing equation (2) by (1)
X2 / X1 = (λD2/d2) x (d1/ λD1)
X2 / X1 = (D2d1)/( D1d2)
X2 / X1 = (D2/D1) x (d1/d2)
X2 / X1 = (2D1/D1) x (d1/1/2 d1) = 2 x 2 = 4
X2 = 4 X1
Ans: The fringe width increased 4 times
Example – 17:
In biprism experiment, interference fringes are observed at a distance of 60 cm from slits illuminated by monochromatic beam of light of wavelength 5460 Å. The distance between the slits is 3 mm. Find the change in fringe width if the distance between the slits is i) increased and ii) decreased by 1 mm.
Given: Distance between screen and sources = 60 cm = 0.6 m, Wavelength of light used = λ = 5460 Å = 5460 x 10-10 m = 5.46 x 10-7 m, Distance between slis = d = 3 mm = 3 x 10-3 m.
Initial Fringe width = X = λD/d = (5.46 x 10-7 x 0.6) / ( 3 x 10-3) = 1.092 x 10-4 m = 0.1092 mm
Part – I: The distance between slits is increased by 1 mm
Given: Initial fringe width = X1 = 0.1092 mm, Initial distance between slits = d1 = 3 mm, New distance between slits = d2 = 3 + 1 = 4mm
To Find: the change in fringe width = ∆X =?
For first case X1 = λD1/d1 ………….. (1)
For second case, X2 = λD2/d2 ………….. (2)
Dividing equation (2) by (1)
X2 / X1 = (λD2/d2) x (d1/ λD1)
X2 / X1 = (D2d1)/( D1d2)
X2 / X1 = d1/d2
X2 = (d1/d2) x X1
X2 = (3/4) x 0.1092 = 0.089
∆X = X1 – X2 = 0.1092 – 0.089 = 0.0273 mm
Part – Ii: The distance between slits is decreased by 1 mm
Given: Initial fringe width = X1 = 0.1092 mm, Initial distance between slits = d1 = 3 mm, New distance between slits = d2 = 3 – 1 = 2mm
To Find: the change in fringe width = ∆X =?
For first case X1 = λD1/d1 ………….. (1)
For second case, X2 = λD2/d2 ………….. (2)
Dividing equation (2) by (1)
X2 / X1 = (λD2/d2) x (d1/ λD1)
X2 / X1 = (D2d1)/( D1d2)
X2 / X1 = d1/d2
X2 = (d1/d2) x X1
X2 = (3/2) x 0.1092 = 0.1638
∆X = X2 – X1 = 0.1683 – 0.1092 = 0.0546 mm
Ans: When the distance between slits is increased by 1 mm, change in fringe width is 0.0273 mm. When the distance between slits is decreased by 1 mm, change in fringe width is 0.0546 mm
Example – 18:
In a biprism experiment, the distance of the slits from the screen is increased by 10% and the separation of slits is decreased by 20%. Find the percentage change in fringe width.
Given: Initial distance between the screen and slits = D1, New distance of screen from slits = D2 = D1 + 10%D1 = 1.10 D1. Initial distance between the slits = d1, New distance between the slits = d2 = d1 – 20%d1 = 0.80 d1
For first case X1 = λD1/d1 ………….. (1)
For second case, X2 = λD2/d2 ………….. (2)
Dividing equation (2) by (1)
X2 / X1 = (λD2/d2) x (d1/ λD1)
X2 / X1 = (D2d1)/( D1d2)
X2 / X1 = (D2/D1) x (d1/d2)
X2 / X1 = (1.10 D1/D1) x (d1/0.80d1)
X2 = (1.10/0.80) x X1
X2 = 1.375 X1
Change in fringe width = ∆X = 1.375X1 – X1 = 0.375 X1
% change in fringe width = (∆X/X1) x 100 = (0.375 X1/X1) x 100 = 37.5
Ans: There is increase of 37.5 % in the fringe width
Example – 19:
In a biprism experiment, interference bands are observed at a distance of one metre from the slit. A convex lens put between the slit and the eye-piece gibes two images of slit 0.7 cm apart, the lens being 30 cm from the slit. Calculate the width of 10 bands if a light of wavelength 5892 Å is used.
Given: Wavelength of light used = 5892 Å = = 5892 x 10-10 m = 5.892 x 10-7 m, Distance between the screen and slit = D = 1m
To Find: Width of 10 bands = 10X =?
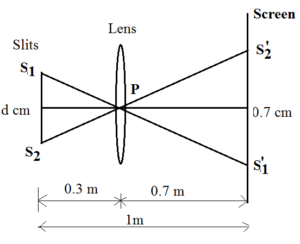
ΔS1‘S2‘ P and S1S2P are similar
d/0.3 = 0.7/0.7
d = 0.3 cm = 0.3 x 10-3 m = 3 x 10-4 m
Fringe width = X = λD/d = (5.892 x 10-7 x 1)/( 3 x 10-4) = 1.964 x 10-4 m = 0.1964 mm
Width of 10 bands = 10 x 0.1964 = 1.964 mm
Ans: The width 10 bands is 1.964 m
Example – 20:
In a biprism experiment, a certain fringe width is observed when the green light of wavelength 5350 Å is used. The distance between the slit and the screen is 1.28 m. What should be the distance between the slit and the screen if the red light of wavelength 6400 Å. is used to get the same fringe width without disturbing the distance between the coherent sources?
Given: Initial wavelength = λ1 = 5350 Å, Initial distance between the slit and screen = D1 = 1.28 m, New wavelength = λ2 = 6400 Å,
To Find: New distance between the slit and screen = D2 =?
The fringe width is given by X = λD/d
For first case X1 = λ1D1/d ………….. (1)
For second case, X2 = λ2D2/d ………….. (2)
Given X1 = X2
λ1D1/d= λ2D2/d
λ1D1 = λ2D2
D2 = (λ1/λ2) x D1
D2 = (5350/6400) x 1.28 = 1.07 m
Ans: The distance between the slit and the screen for the red light is 1.07 m
Example – 21:
In biprism experiment when the slit is illuminated by light of wavelength 5890 Å, twenty fringes occupied 2.3 cm on the screen. When this light is substituted by another monochromatic light, thirty fringes occupied 2.8 cm on the screen. Find the wavelength of this light.
Given: Initial wavelength = λ1 = 5890 Å, Initial fringe width = X1 = 2.3/20 cm, New fringe width = X2 = 2.8/30 cm,
To Find: New wavelength = λ2 =?
For first case X1 = λ1D/d ………….. (1)
For second case, X2 = λ2D/d ………….. (2)
Dividing equation (2) by (1)
X2 / X1 = (λ2D/d) x (d/ λ1D)
X2 / X1 = λ2/λ1
λ2 = (X2/X1) x λ1 = ((2.8/30)/(2.3/20)) x 5890
λ2 = (X2/X1) x λ1 = (5.6/6.9) x 5890 = 4780 Å
Ans: The new wavelength used is 4780 Å
Example – 22:
In a biprism experiment, fringes were obtained with a monochromatic source of light. The eye-piece was kept at a distance of 1 m from the slit and the bandwidth was measured. When another monochromatic source was used without disturbing the arrangement, the same bandwidth was obtained when the eye-piece was at 80 cm from the slit. Calculate the ratio of wavelengths of light from the two sources.
Given: Initial distance between the slit and screen = D1 = 1 m, New distance between the slit and screen = D2 = 80 cm = 0.8 m
To Find: Ratio of wavelengths = λ1/λ2 =?
For first case X1 = λ1D1/d ………….. (1)
For second case, X2 = λ2D2/d ………….. (2)
Given X1 = X2
λ1D1/d= λ2D2/d
λ1D1 = λ2D2
λ1/λ2 = D2/D1 = 0.8/1 = 8/10 = 4/5
Ans: The ratio of wavelengths used is 4:5
Previous Topic: More Problems on Fringe Width and Change of Fringe Width
For More Topics in Physics Click Here