Calorimetry

Science > Physics > Thermometry > Numerical Problems on Temperature Scales

In the last article, we have seen the concept of specific heat, latent heat and we have solved numerical problems on the concept. In this article, we shall study to solve problems on heat exchanges involving calorimeter.

Heat Capacity of a Body:

It is easier to express the heat capacity of the whole body rather than 1 kg as used in the definition of the specific heat of a substance. The heat capacity of a body is defined ad the amount of heat required to raise its temperature by oC. This quantity is also known a thermal capacity of a body. We have

Q = m c Δ T

Heat capacity = m c x 1 = mc

Hence heat capacity of a body (solid or liquid) is equal to the product of its mass and specific heat. The S.I. unit of heat capacity is J/K. Thus the greater the mass of a body, the greater is its heat capacity.

Water Equivalent of a Body:

The water equivalent of a body is defined as the mass of water that will absorb or lose the same amount of heat as the body for the same rise or fall in temperature. S.I. unit of water equivalent is kg and in cgs system is g.

We have for a body, Q = m c Δ T ……. (1)

Let ‘w’ be water equivalent of the body

Q = w Δ T ……. (2)

From equations (1) and (2) we get

w Δ T = m c Δ T

w = mC

Thus the water equivalent of a body is numerically equal to the product of the mass of the body and its specific heat. Thus water equivalent of a body and its heat capacity are numerically equal.

Law of Heat Exchange:

When a hot body is mixed or kept in contact with a cold body, the hot body loses heat and its temperature falls. On the other hand, the cold body absorbs the heat lost by the hot body and the temperature of the cold body increases. A state will reach when the whole mixture shows a common temperature. This final temperature of the mixture will lie between the original temperatures of the hot body and the cold body. If this system is completely isolated that is there is no flow of energy into the system or out of the system, then by the law of conservation of energy, the heat lost by one body is equal to the heat gained by the other body. This relation is known as the law of heat exchange.

Thus by the law of heat exchange, Heat lost = Heat gained.

Calorimetry:

Calorimetry is an experimental technique for the quantitative measurement of heat exchange. For this purpose instrument called a calorimeter is used.

A calorimeter mainly consists of a metallic cylindrical vessel made of materials that are good conductors of electricity such as copper and aluminium etc. with a stirrer and a lid. The stirrer is used for stirring the contents of the vessel. This vessel is heat insulated to prevent heat loss to the surroundings. A thermometer can be inserted through one opening to measure the change in the temperature of the contents of the vessel. A calorimeter is used to determine the specific heat of a substance by a technique called the ‘method of mixtures’. The substance whose specific heat is to be found is heated to a high temperature which is accurately measured. The substance is then placed in the calorimeter containing a known mass of water and its temperature is also known. The mixture is stirred constantly, till the mixture attains the final common temperature. By the principle of heat exchange, the heat lost by the substance will be gained by the water and calorimeter. The specific heat of a substance is found using the following formula:

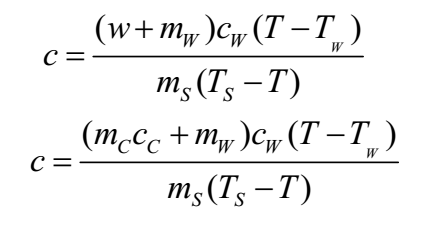
Where, c = Specific heat of the substance

w = water equivalent of calorimeter

m_W = mass of water

c_W = Specific heat of water

T_W = Temperature of water

T = temperature of the mixture

m_S = mass of substance

T_S = Temperature of substance

m_c = Mass of the calorimeter

c_c = Specific heat of material of the calorimeter

If we consider the loss of heat ΔQ in the experiment, the formula can be written as:

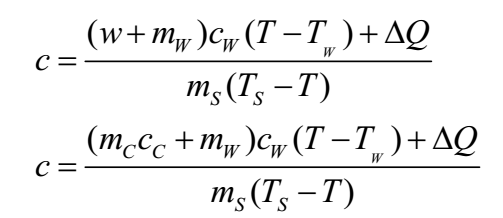
Numerical Problems:

Example 01:

A copper calorimeter weighing 40 g contains 120 g of water at 20^oC. When a copper sphere weighing 100 g and 120 ^oC is dropped into the calorimeter, the temperature of the mixture rises to 27 ^oC. Find the sp. Ht. of copper and the thermal capacity of the calorimeter assuming the heat losses in the experiment amount to 62 cal.

Given: Mass of calorimeter = m_C = 40g, Mass of water m_W = 120 g, Initial temperature of water  and the calorimeter = T_W = 20^oC, Mass of copper sphere = m_Cu = 100 g, Temperature of copper sphere = T_Cu = 120^oC, Temperature of mixture = T = 27^oC, Heat lost in experiment = ΔQ = 62 cal

To Find Sp. Ht. of copper = c_cu =?, Thermal heat =?

Solution:

By the law of heat exchange, Heat lost = Heat gained.

Heat lost by the copper sphere = Heat gained by calorimeter and water =

∴ m _Cu c_Cu (T_Cu – T) = (m_C c_Cu + M_W) (T – T_W)   + Δ Q

∴ 100 x c_Cu (120 – 27) = (40 x c_Cu + 120) (27 – 20)   + 62

∴ 100 x c_Cu x 93 = (40 x c_Cu + 120) (7)   + 62

∴ 9300 x c_Cu = 280 x c_Cu + 840   + 62

∴ 9300 x c_Cu – 280 x c_Cu = 902

∴ 9020 x c_Cu = 902

∴ c_Cu = 0.1 cal/g/^oC

∴ c_Cu = 0.1 x 4186 J/kg/K = 418.6 J/kg/K

Thermal capacity of calorimeter = m_C c_Cu =40 x 0.1 = 4 cal /^oC

Thermal capacity of calorimeter = 4 x 4.186 = 16.744 J/K

Ans: Specific heat of copper is 0.1 cal/g/^oC or 418.6 J/kg/K and thermal capacity of calorimeter is 4 cal /^oC or 16.744 J/K

Example 02:

A calorimeter weighs 100 g and contains 50 g of water at 10 ^oC. On adding 36 g of water at 50 ^oC into the calorimeter, the highest temperature of the mixture is found to be 25 ^oC. Find the water equivalent of the calorimeter and the sp. Ht. of the material of calorimeter.

Given: Mass of calorimeter = m_C = 100g, Mass of water m_W = 50 g, Initial temperature of water and the calorimeter = T_W = 10^oC, Mass of additional water = m_s = 36 g, Temperature of added water = T_s = 50^oC, Temperature of mixture = T = 25^oC

To Find: Sp. Ht. of material of calorimeter = c =?, water equivalent of copper = ?

Solution:

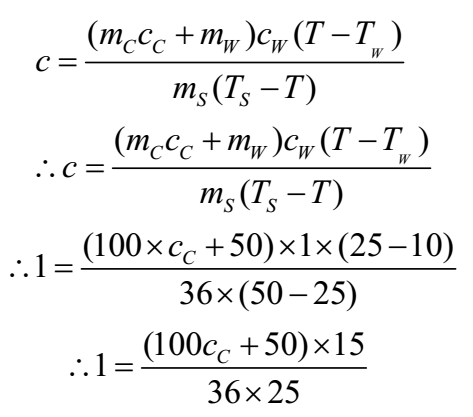
∴ 900 = 1500 + 750

∴ 1500 c_C = 150

∴ c_C = 0.1 cal/g/^oC

∴ c_C = 0.1 x 4186 J/kg/K = 418.6 J/kg/K

Water equivalent of calorimeter = m_C c_C = 100 x 0.1 =  10 g

Ans: Specific heat of copper is 0.1 cal/g/^oC or 418.6 J/kg/K and water equivalent of calorimeter is 10 g.

Example 03:

A piece of lead at 99 ^oC is placed in a calorimeter containing 200 g of water at 15 ^oC. The temperature after stirring is 21 ^oC. Calculate the thermal capacity of the lead piece if the water equivalent of the calorimeter is 9.3 g.

Given: Water equivalent of calorimeter = w = 9.3 g, Mass of water m_W = 200 g, Initial temperature of water and the calorimeter = T_W = 15^oC, Mass of lead piece = m_s = 36 g, Temperature of lead piece = T_s = 99^oC, Temperature of mixture = T = 21^oC

To Find: Thermal capacity of lead piece = m_sc_s =?

Solution:

Ans: The thermal capacity of the lead piece is 16.1 cal/^oC.

Example 04:

A 0.2 kg metal price at 149 ^oC is dropped in a copper calorimeter (water equivalent 0.5 kg) containing 200  of water at 29 ^oC. The final temperature of the mixture is 49 ^oC. Find the sp. ht of the metal. Neglect effect of the surroundings. The density of water = 10³ kg/m³. Sp.ht. of water = 4200 J/kg/K. 

Given: Water equivalent of calorimeter = w = 0.5 kg, volume of water V_W = 200 cm³, Initial temperature of water and the calorimeter = T_W = 29^oC, Mass of metal piece = m_s = 0.2 kg, Temperature of metal piece = T_s = 149^oC, Temperature of mixture = T = 49^oC, Density of water = 10³ kg/m³, Sp.ht. of water = 4200 J/kg/K. 

To Find: Specific heat of metal = c_s =?

Solution:

Volume of water = v_W = 200 cm³ = 200 x 10^-6 m³

Mass of water m_W = 200 x 10^-6 x 10³ = 0.2 kg

Ans: Specific heat of metal is 2940 J/kg/K.

Example 05:

To determine the specific heat of a new alloy, its 0.150 kg sample was heated to 540 ^oC and then quickly placed in 400g of water at 10 ^oC which is contained in 200 g of aluminium calorimeter cup. The final temperature of the mixture is 30.5 ^oC. Calculate the specific heat of the alloy if that of aluminium is 0.22 cal/g/^oC.

 Given: Mass of copper calorimeter = m_C = 200g, Specific heat of aluminium = c_C=  0.22 cal/g/^oC, Mass of water m_W = 400 g, Initial temperature of water and the calorimeter = T_W = 10 ^oC, Mass of alloy piece = m_s = 0.150 kg = 150 g, Temperature of alloy piece = T_s = 540^oC, Temperature of mixture = T = 30.5 ^oC, Density of water = 10³ kg/m³, Sp.ht. of water = 4200 J/kg/K. 

To Find: Specific heat of alloy = c_s =?

Solution:

Heat lost by alloy piece = m_S c_S (T_S – T)

∴ Heat lost by alloy piece = 150 x  c_S  x(540 – 30.5)

∴ Heat lost by alloy piece = 150 x  c_S  x509.5

∴ Heat lost by alloy piece = 76430 c_S  cal …………. (1)

Heat gained by water and calorimeter = (m_Cc_C + m_W) x c_W x (T – T_W)

∴ Heat gained = (200 x 0.22 + 400) x 1 x (30.5 – 10)

∴ Heat gained = (44 + 400) x 1 x 20.5

∴ Heat gained = 444 x 1 x 20.5 = 9102 cal ……….. (2)

By the principle of heat exchange

Heat lost = Heat gained

76430 c_S  = 9102

c_S  = 9102/76430 = 0.1191 = 0.119 cal/g/^oC

Ans: Specific heat of alloy is 0.119 cal/g/^oC