Conversion Table:
| Sr. No. | From | To | Multiplying Factor |
| 1 | mm | m | x 10-3 |
| 2 | cm | m | x 10-2 |
| 3 | cm | mm | x 10 |
| 4 | mm | cm | x 10-1 |
| 5 | m | cm | x 102 |
| 6 | m | mm | x 103 |
| 7 | km hr-1 | m s-1 | x (5/18) |
| 8 | m s-1 | km hr-1 | x (18/5) |
| 9 | g cm-3 | kg m-3 | x 103 |
| 10 | kg m-3 | g cm-3 | x 10-3 |
| 11 | kg | g | x 103 |
| 12 | g | kg | x 10-3 |
| 13 | m2 | cm2 | x 104 |
Q2.1: Fill in the blanks
(a) The volume of a cube of side 1 cm is equal to …….. m3.
Solution:
1 cm = 10-2 m
Volume of the cube = V = 1 cm3
∴ V = 1 cm3 = 1 cm x 1 cm x 1cm
∴ V = (10-2 m) x (10-2 m) x (10-2 m)
∴ V = 10-6 m3
Ans: The volume of a cube of side 1 cm is equal to 10-6 m3
(b) The surface area of a solid cylinder of radius 2.0 cm and height 10.0 cm is equal to ……… mm2.
Solution:
r = 2 cm = 2 x 10 mm = 20 mm
h = 10 cm = 10 x 10 mm = 100 mm
The total surface area of a cylinder of radius r and height h is
S = 2 π r (r + h)
∴ S = 2 x 3.14 x 20 (20 + 100)
∴ S = 2 x 3.14 x 20 x 120 = 1.5 x 104 mm2
Ans: The surface area of a solid cylinder of radius 2.0 cm and height 10.0 cm is equal to 1.5 x 104 mm2.
(c) A vehicle moving with a speed of covers 18 km h-1 covers ……. m in 1 s
Solution:
Speed = 18 km h-1 = 18 x (5/18) = 5 m s-1
Now, Distance = Speed x Time = 5 x 1 = 5 m
Ans: A vehicle moving with a speed of covers 18 km h-1 covers 5 m in 1 s
(d) The relative density of lead is 11.3. Its density is ….…. g cm-3 or …….. kg m-3.
Solution:
Relative density = Density of substance/Density of water
∴ Density of lead = Relative density of lead x Density of water
∴ Density of lead = 11.3 x 1 = 11.3 g cm-3 = 11.3 x 103 kg m-3
Ans: The relative density of lead is 11.3. Its density is 11.3 g cm-3 or 11.3 x 103 kg m-3.
Q 2.2: Fill in the blanks by suitable conversion of units
(a) 1 kg m2 s-2 = ………. g cm2s-2
Solution:
1 kg m2 s-2 = 1 x (103 g) (102 cm) 2 (s) -2
∴ 1 kg m2 s-2 = 1 x (103 g) (104 cm2)(s-2)
∴ 1 kg m2 s-2 = 107 g cm2s-2
(b) 1 m = …… ly
Solution:
1 ly = 9.46 x 1015 m
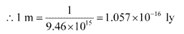
∴ 1m = 1.057 x 10-16 ly
(c) 3.0 m s-2 = ……. km h-2
Solution:
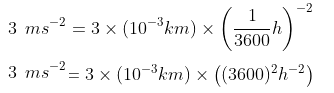
∴ 3.0 m s-2 = 3.89 x 104 km h-2
(d) G = 6.67 x 10-11 Nm2 kg-2 = cm3 s-2 g-1
Solution:
G = 6.67 x 10-11 N m2 kg-2
∴ G = 6.67 x 10-11 (kg m s-2) m2 kg-2
∴ G = 6.67 x 10-11 m3 s-2 kg-1
∴ G = 6.67 x 10-11 (102 cm)3 s-2 (103 g)-1
∴ G = 6.67 x 10-11 (106 cm3) s-2 (10-3 g-1)
∴ G = 6.67 x 10-8 cm3 s-2 g-1
Q2.3: Solve the following.
A calorie is a unit of heat (energy in transit) and it equals about 4.2 J where 1 J = 1 kg m2 s–2. Suppose we employ a system of units in which the unit of mass equals α kg, the unit of length equals β m, the unit of time is γ s. Show that a calorie has a magnitude 4.2 α–1 β–2 γ2 in terms of the new units.
Solution:
Method – I:
Given new unit of mass is α kg.
Thus, 1 kg = (1/ α) = α -1
Given new unit of length is β m.
Thus, 1 m = (1/ β) = β -1
Given new unit of time is γ s.
Thus, 1 s = (1/ γ) = γ -1
Given 1 cal = 4.2 J = 4.2 kg m2 s–2
∴ 1 cal = 4.2 (α -1) (β -1)2 (γ -1)–2
∴ 1 cal = 4.2 α -1 β -2 γ 2 (Proved)
Method – II:
Given 1 cal = 4.2 J = 4.2 kg m2 s–2
∴ a = 1, b = 2, c = -2
We have n1u1 = n2u2
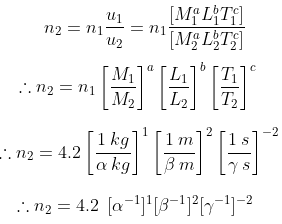
∴ 1 cal = 4.2 α -1 β -2 γ 2 (Proved)
Q 2.4: Solve the following.
Explain this statement clearly: “To call a dimensional quantity ‘large’ or ‘small’ is meaningless without specifying a standard for comparison”. In view of this, reframe the following statements wherever necessary:
(a) An atom is a very small object in comparison to a soccer ball.
(b) A jet plane moves with a speed greater than that of a bicycle.
(c) Mass of Jupiter is very large as compared to the mass of a cricket ball.
(d) The air inside this room contains a large number of molecules as compared to that present in a geometry box.
(e) A proton is more massive than an electron.
(f) Speed of sound is less than the speed of light.
Solution:
The given statement is correct because a process of measurement involves a comparison process. To get exact idea about the magnitude of a dimensional quantity, we have to specify a standard of comparison. For example, the statement mass of whale is large is meaningless. To correct it we have to specify that the mass of whale is large in comparison with any other animal.
The reframed statements are as follows:
- Statement is not correct. The reframed statement is: The size of an atom is much smaller than the sharp tip of a needle.
- Statement is not correct. The reframed statement is: A jet plane moves with a far greater speed than a superfast train.
- Statement is not correct. The reframed statement is: The mass of Jupiter is very large compared to that of the Earth.
- Statement is not correct. The reframed statement is: The air inside this room contains a very large number of molecules as compared to that in a balloon.
- The statement is correct.
- The statement is correct.
Q 2.5: Solve the following.
A new unit of length is chosen such that the speed of light in vacuum is unity. What is the distance between the Sun and the Earth in terms of the new unit if light takes 8 min and 20 s to cover this distance?
Given that in the new unit, speed of light = 1 unit
Time taken, t = 8 min 20 s = 8 x 60 + 20 = 500 s
Distance between the Sun and the Earth
= Speed of light x Time taken by light to cover the distance
∴ Distance between the Sun and the Earth = 1 new unit of length x 500 s
= 500 new units of length
Q 2.6 Solve the following.
Which of the following is the most precise device for measuring length:
(a) a vernier callipers with 20 divisions on the sliding scale
(b) a screw gauge of pitch 1 mm and 100 divisions on the circular scale
(c) an optical instrument that can measure length to within a wavelength of light ?
Solution:
(a) Least count of vernier callipers
Least Count = 1 M.S.D. – 1 V.S.D.
∴ Least Count = 1 M.S.D. – (19/20) M.S.D. = (1/20) M.S.D.
∴ Least Count = (1/20) x 1mm = 0.05 mm = 0.005 cm.
(b) Least count of screw gauge
Least count = pitch /no. of divisions on circular scale
∴ Least count = 1/100 mm = 0.01 mm = 0.001 cm
(c) Least count of an optical device
Least count of instrument = Wavelength of light
∴ Least count = λ = 10-7 m = 10-5 cm (approx.)
∴ Least count = 0.00001 cm
A device with minimum least count is the most suitable to measure length precisely. Hence, an optical instrument having the minimum least count is the most suitable device to measure length precisely.
Q 2.7 Solve the following.
A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5 mm. What is the estimate on the thickness of hair?
Magnification of the microscope = 100
Average width of the hair in the field of view of the microscope = 3.5 mm
We have magnification = Observed thickness/Actual thickness
∴ Actual thickness = Observed thickness/ Magnification
∴ Actual thickness of hair = 3.5/100 = 0.035 mm
Q 2.8 Solve the following.
Answer the following:
(a)You are given a thread and a metre scale. How will you estimate the diameter of the thread?
(b)A screw gauge has a pitch of 1.0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale?
(c) The mean diameter of a thin brass rod is to be measured by vernier callipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only?
Solution:
Solution to question (a)
Wrap the thread on a uniform smooth rod in such a way that the coils thus formed are very close to each other. Measure the length (L) of the thread using a metre scale. Count number of turns (N) of thread in this length. The diameter of the thread is given by the relation,
Diameter of thread = L/N

Solution to question (b)
Least count of screw gauge = Pitch / Number of divisions on the circular scale.
From the formula we can see that by increasing the number of divisions on the circular scale, lower least count can be obtained. But when more number of divisions are made, the division marks will be very close to each other and due to low resolution and limitation of human eye reading cannot be precisely read. Thus accuracy may be lost. Thus increasing the number divisions of the circular scale will increase its accuracy to a certain extent only.
Solution to question (c)
When a larger number of readings are taken, their mean value will be closer to the true value and hence the random errors are minimized. Thus a large number of observations will give more reliable result than small number of observations.
Q 2.9 Solve the following.
The photograph of a house occupies an area of 1.75 cm2 on a 35 mm slide. The slide is projected on to a screen, and the area of the house on the screen is 1.55 m2. What is the linear magnification of the projector-screen arrangement?
Solution:
Area of the house on the slide = 1.75 cm2
Area of the image of the house formed on the screen
= 1.55 m2 = 1.55 x 104 cm2
Arial magnification = Area of image / Area of object
∴ Arial magnification = (1.55 x 104 )/1.75 = 8.857 x 103

∴ Linear magnification = 94.11
Q 2.10 Solve the following.
State the number of significant figures in the following : (a) 0.007 m2, (b) 2.64 × 1024 kg, (c) 0.2370 g cm–3, (d) 6.320 J (e) 6.032 N m–2, (f) 0.0006032 m2
| Sr. No. | Quantity | Significant Figures |
| (a) | 0.007 m2 | 1 |
| (b) | 2.64 × 1024 kg | 3 |
| (c) | 0.2370 g cm–3 | 4 |
| (d) | 6.320 J | 4 |
| (e) | 6.032 N m–2 | 4 |
| (f) | 0.0006032 m2 | 4 |
Analysis:
(a) 0.007 is less than 1. If number is less than 1, then all zeros on right side of decimal point but left to the first non zero number are not significant. This left with 7 only. Thus number of significant figures is 1.
(b) in 2.64 × 1024, the power of 10 is irrelevant in the determination of the significant figure. 2, 6, and 4 are significant. Thus number of significant figures is 3.
(c) 0.2370 is less than 1. If number is less than 1, then all zeros on right side of decimal point but left to the first non zero number are not significant. 2, 3, 7, and 0 are significant. Thus number of significant figures is 4.
(d) In 6.320, 6, 3, 2, and 0 are significant. Thus number of significant figures is 4.
(e) In 6.032, 6, 0, 3, and 2 are significant. Thus number of significant figures is 4.
(f) 0.0006032 is less than 1. If number is less than 1, then all zeros on right side of decimal point but left to the first non zero number are not significant. 6, 0, 3, and 2 are significant. Thus number of significant figures is 4.
Q 2.11 Solve the following.
The length, breadth and thickness of a rectangular sheet of metal are 4.234 m, 1.005 m and 2.01 cm respectively. Give the area and volume of the sheet to correct significant figures.
Solution:
Analysis:
Length l = 4.234 m (4 significant figures) , b = 1.005 m (4 significant figures) and thickness = t = 2.01 cm = 0.0201 m (3 significant figures). Thus 3 is the least number of significant figures. Hence the final answer should have 3 significant figures only.
Surface Area = 2 x ( l x b + b x t + l x t)
∴ Surface Area = 2 x ( 4.234 x 1.005 + 1.005 x 0.0201 + 4.234 x 0.0201 )
∴ Surface Area = 8.7209478 = 8.72 m2
∴ Volume = l x b x h
∴ Volume = 4.234 x 1.005 x 0.0201 = 0.085528917 = 0.0855 m3.
Q 2.12 Solve the following.
The mass of a box measured by a grocer’s balance is 2.3 kg. Two gold pieces of masses 20.15 g and 20.17 g are added to the box. What is (a) the total mass of the box (b) the difference in the masses of the pieces to correct significant figures?
Solution:
Analysis:
Mass of box measured by grocer’s balance is 2.3 kg ( 2 significant figures), mass of gold pieces are 20.15 g and 20.17 g (4 significant figures each). Thus Final answer should have least i.e. 2 significant figures.
(a) Total mass of the box with gold pieces = (2.3 + 0.02017 + 0.02015) kg = 2.34032 kg = 2..3 kg ( 2 significant figures)
(b) Difference of mass of gold pieces = 20.17 – 20.15 = 0.02 g (Correct to two decimals)
Q 2.13 Solve the following.
A physical quantity P is related to four observables a, b, c and d as follows:

The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2%, respectively. What is the percentage error in the quantity P? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result?
Solution:

As the error lies in first decimal place, the answer should be rounded off to first decimal place. Hence, we shall express the value of P = 3.763 after rounding it off as P = 3.8
Q 2.14 Solve the following.
A book with many printing errors contains four different formulas for the displacement y of a particle undergoing a certain periodic motion:

(a = maximum displacement of the particle, v = speed of the particle, T = time-period of motion)Rule out the wrong formulas on dimensional grounds.
Solution:

The dimensions of the argument of trigonometric function is
[2πt/T] = [t]/[T] = [T][T] = [M0L0T0] = Dimensionless
Trigonometric function is dimension less
By principle of homogeneity, equation to be dimensionally correct, dimensions of both side should be the same.
[L.H.S.] =[y] = [M0L1T0] ……… (1)
[R.H.S.] = [a] [sin(2 π t/T)] = [M0L1T0] [M0L0T0]
∴ [R.H.S.] = [M0L1T0] ……… (2)
From equations (1) and (2) we have
[L.H.S.] = [R.H.S.]
Thus given formula is dimensionally correct.

The dimensions of the argument of trigonometric function is
[vt] = [v] [t] = [ M0L1T-1 ][ M0L0T1 ] = [M0L1T0] = No dimensionless quantity
Thus the argument of trigonometric function is not dimensionless quantity. Hence the formula is dimensionally not correct.

The dimensions of the argument of trigonometric function is
[t/a] = [t] /[a] = [ M0L0T1 ][ M0L1T0 ] = [M0L-1T1] = No dimensionless quantity
Thus the argument of trigonometric function is not dimensionless quantity. Hence the formula is dimensionally not correct.

The dimensions of the argument of trigonometric function is
[2πt/T] = [t]/[T] = [T][T] = [M0L0T0] = Dimensionless
Trigonometric function is dimension less
By principle of homogeneity, equation to be dimensionally correct, dimensions of both side should be the same.
[L.H.S.] =[y] = [M0L1T0] ……… (1)
[R.H.S.] = [a] [sin(2 π t/T) + cos (2 π t/T) ]
∴ [R.H.S.] = [M0L1T0] [M0L0T0]
∴ [R.H.S.] = [M0L1T0] ……… (2)
From equations (1) and (2) we have
[L.H.S.] = [R.H.S.]
Thus given formula is dimensionally correct.
Q 2.15 Solve the following.
A famous relation in physics relates ‘moving mass’ m to the ‘rest mass’ m0 of a particle in terms of its speed v and the speed of light c. (This relation first arose as a consequence of special relativity due to Albert Einstein). A boy recalls the relation almost correctly but forgets where to put the constant c. He writes

Guess where to put the missing c.
Solution:

L.H.S. is a pure ratio, hence it is a dimensionless quantity. By principle of homogeneity the R.H.S. must be dimensionless quantity.
Thus quantity (1 – v2) is dimensionless quantity. The first part in bracket is dimensionless, hence second part must be dimensionless i.e. velocity v must be divided by another velocity (c). Hence corrected formula is as follows:

Q 2.16 Solve the following.
The unit of length convenient on the atomic scale is known as an angstrom and is denoted by Å: 1 Å = 10-10 m. The radius of a hydrogen atom is about 0.5 Å. What is the total atomic volume in m3 of a mole of hydrogen atoms?
Solution:
Radius of hydrogen atom = 0.5 Å = 0.5 x 10-10 m
Assuming a hydrogen atom as a perfect sphere, Volume of one hydrogen atom
V = 4/3 πr3
V = 4/3 x 3.14 x (0.5 x 10-10) m3 = 5.233 x 10-31 m3
According to Avogadro’s hypothesis, one mole of hydrogen contains 6.023 x 1023 atoms.
Atomic volume of 1 mole of hydrogen atoms
= 6.023 x 1023 x 5.233 x 10-31
= 3.152 x 10-7m3 = 3 x 10-7m3
Q 2.17 Solve the following.
One mole of an ideal gas at standard temperature and pressure occupies 22.4 L (molar volume). What is the ratio of molar volume to the atomic volume of a mole of hydrogen? (Take the size of hydrogen molecule to be about 1 Å .) Why is this ratio so large?
Solution:
Diameter of hydrogen molecule = 1 Å
Radius of hydrogen molecule = 0.5 Å = 0.5 x 10-10 m
Assuming a hydrogen molecule as a perfect sphere, Volume of one hydrogen molecule
V = 4/3 πr3
V = 4/3 x 3.14 x (0.5 x 10-10) m3 = 5.233 x 10-31 m3
According to Avogadro’s hypothesis, one mole of hydrogen contains 6.023 x 1023 molecules.
Actual volume of 1 mole of hydrogen atoms
= 6.023 x 1023 x 5.233 x 10-31
Vactual= 3.152 x 10-7m3
Volume occupied by hydrogen gas at S.T.P. = Voccupied = 22.4 L = 22.4 x 10-3 m3
Required ratio = Voccupied / Vactua = 22.4 x 10-3 / 3.152 x 10-7
Required ratio = 7.108 x 104 = 7.1 x 104
The ratio is very large. This is because the intermolecular separation in the gas is very large compared to the size of a hydrogen molecule.
Q 2.18 Solve the following.
Explain this common observation clearly: If you look out of the window of a fast moving train, the nearby trees, houses etc., seem to move rapidly in a direction opposite to the train’s motion, but the distant objects (hill tops, the Moon, the stars etc.) seem to be stationary. (In fact, since you are aware that you are moving, these distant objects seem to move with you).
Q 2.19 Solve the following.