Science > Physics > Force > Centre of Mass and Centre of Gravity
In this article. we shall study the concept of centre of mass and centre of gravity of a body and methods to locate them.
Concept of Centre of Mass:
The entire mass of a body is supposed to be concentrated at a single point and the external force acting on the body is applied at that point. This point is called the centre of mass of the body. Its position depends on the distribution of the different particles in the body. For symmetrical bodies, the centre of mass is situated at the point of symmetry.
Centre of Mass System of Discrete Masses:
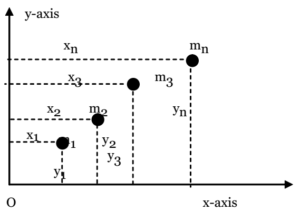
Consider system discrete masses consisting of ‘n’ number of mass points having masses m1, m2, m3, m4, ……..mn situated at a distance of x1, x2, x3, x4, ………….xn respectively from Y-axis and at a distance of y1, y2, y3, y4, ……..yn respectively from X-axis of the rectangular Cartesian system of axes. Let C be the centre of mass of the system. Let x be the distance of point C from Y-axis and y be the distance of point C from X-axis. Then, the position of the centre of mass of a system is given by
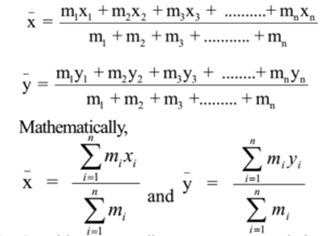
Consider system of discrete masses consisting of ‘n’ number of mass points having masses m1, m2, m3, m4, ……..mn situated at points having position vectors r1, r2, r3, r4, …….rn respectively from origin ‘O’ of the rectangular Cartesian system of axes. Then, the position of the centre of mass of a system is given by

If the body is assumed to be made up of continuous mass, then the process of summation can be replaced by the process of integration with proper limits. Limits depend on the shape and distribution of the mass of the body.

The Concept of the Centre of Gravity:
A rigid body can be considered as a collection of a large number of discrete particles. Each particle is attracted by the earth with a force, which is equal to the weight of that particle. These forces of attraction act vertically downward. The resultant force of these downward forces is equal to the weight of the whole body. This resultant gravitational force always acts through a definite point, called the centre of gravity (C.G.) of the body.
The centre of gravity of a body is defined as a point through which the resultant weight of the body always acts whatever may be the position of the body.
For bodies having symmetrical shapes, the centre of gravity is at their point of symmetry. For almost all practical purpose the centre of mass of body coincides with its centre of gravity. For bodies of small sizes the centre of mass and centre of gravity coincide but for bodies of larger size centre of gravity lies below the centre of mass.
Relative Positions of Centre of gravity and Centre of Mass of a Body:
For bodies having symmetrical shapes, the centre of gravity is at their point of symmetrical. For almost all practical purpose the centre of mass of body coincides with its centre of gravity.
However, in the case of very large objects like mountains or lakes the acceleration due to gravity is not the same for all the particles it is greater for the particles nearer the surfaces of the earth and less for the particles away from the surface of the earth. Thus For bodies of small sizes, the centre of mass and centre of gravity coincide but for bodies of larger size centre of gravity lies below the centre of mass.
Numerical Problems:
Example – 01:
Locate the centre of mass of two spheres of the same material and of radii 0.02 m and 0.04 m kept with their centres 0.09 m apart.
Given: R1 = 0.02 m = 2 cm, R2 = 0.04 m = 4 cm, r = 0.09 m = 9 cm
To Find: Position of C. M.
Solution:
Let x be the distance of the centre of mass of the system from the centre of the smaller sphere.

Ans: The distance of the C.M. is 0.08 m from the centre of the smaller sphere.
Example – 02:
A 2 kg sphere has its centre located at x = -3 m and 8 kg sphere has its centre located at x = 2m. Find the position of their centre of mass.
Given: m1 = 2kg, x1 = – 3 m, m2 = 8 kg, x2 = 2 m
To Find: Position of C.M.
Solution:
Let x be the distance of the centre of mass of the system on the reference system

Ans: The C.M. of the system is at x = + 1 m
Example – 03:
The coordinates of three particles each of mass 1 kg are (x,0)m, (x/2,y) m and (0,0) m respectively. Find the coordinates of the centre of mass.
Given: m1 = 1 kg, x1 = x, y1 = 0, m2 = 1 kg, x2 = x/2, y2 = y, m3 = 1 kg, x3 = 0, y3 = 0,
To Find: Coordinates of C.M.
Solution:


Ans : The coordinates of C. M. are (x/2,y/3) m
Example – 04:
For a system of point masses m1, m2 and m3 kept at the vertices of a triangle AOB as shown, find the coordinates of the centre of mass.

Given: m1 at (x1, y1),m2 at (x2, 0), and m3 at (0, 0)
To Find: Position of the C.M.
Solution:


Ans: xcm = (m1x1+ m2x2)/(m1+ m2 + m3); ycm = (m1y1)/(m1+ m2 +m3)
Example – 05:
The centres of three spherical masses of 2 kg, 4kg and 6kg have coordinates (3,0) m, (6, 0) m and (2, -8) m respectively. Find the centre of mass of the system in vector form.
Given: m1 = 2 kg, x1 = 3, , y1 = 0, m2 = 4 kg, x2 = 6, y2 = 0, m3 = 6 kg, x3 = 2, y3 = -8,
To Find: Position vector of C.M.
Solution:


Ans: Position vector of the C.M. of the system r = 3.5 i – 4 j
Example – 06:
Four masses of 1 kg, 2 kg, 3 kg and 4kg are kept at (0,0) m, (1,0) m, (1,1) and (0,1) m respectively. Locate the centre of mass by the position vector.
Given: m1 = 1 kg, x1 = 0, , y1 = 0, m2 = 2 kg, x2 = 1, y2 = 0, m3 = 3 kg, x3 = 1, y3 = 1, m4 = 4 kg, x4 = 0, y4 = 1,
To Find: Position vector of C.M.
Solution:


Ans: Position vector of the centre of mass of the system r = 0.5 i – 0.7 j
Previous Topic: The Concept of Couple
For More Topics in Physics Click Here