Science > Physics > Circular Motion > Numerical Problems on Centripetal Force – 02
Example – 19:
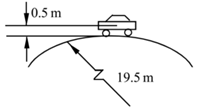
The vertical section of a road over a bridge in the direction of its length is in the form of an arc of a circle of radius 19.5 m. Find the greatest velocity at which a car can cross the bridge without losing contact with the road at the highest point if the c.g. of the car is 0.5 m from the ground.
Given: Radius of circle = r = 19.5 + 0.5 = 20 m,
To find: velocity of car = v =?
Solution:
At the highest point, the centrifugal force and weight of the car are equal in magnitude.
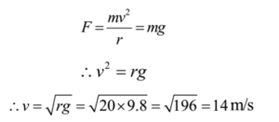
Ans: The velocity of car = 14 m/s
Example – 20:
A flyover bridge is in the form of a circular arc of radius 30 m. Find the limiting speed at which a car can cross the bridge without losing contact with the road at the highest point. Assume the centre of gravity of the car to be 0.5 m above the road.
Given: Radius of circle = r = 30 + 0.5 = 30.5 m,
To find: velocity of car = v =?
Solution:

At the highest point, the centrifugal force and weight of the car are equal in magnitude.

Ans: The velocity of car = 17.3 m/s
Example – 21:
A motorcyclist rides in a vertical circle in a hollow sphere of radius 3 m. Find the minimum speed required so that he does not lose contact with the sphere at the highest point. Also, find its angular speed.
Given: Radius of hollow sphere = r = 3 m,
To find: Minimum speed required = v = ?, Angular speed = ω = ?
Solution:
At the highest point, the centrifugal force and weight of the motorcyclist and motorcycle are equal in magnitude.

Ans: The velocity of car = 5.42 m/s, Angular speed = 1.807 rad/s.
Example – 22:
A motorcyclist rides in a vertical circle in a hollow sphere of radius 12.8 m. Find the minimum speed required so that he does not lose contact with the sphere at the highest point.
Given: Radius of sphere = r = 12.8 m,
To find: Minimum speed = v =?
Solution:
At the highest point, the centrifugal force and weight of the motorcyclist and motorcycle are equal in magnitude.

Ans: Minimum speed of motorcycle = 11.2 m/s
Example – 23:
An object of mass 100 g moves around the circumference of a circle of radius 2m with a constant angular speed of 7.5 rad/s. Compute its linear speed and force directed towards centre.
Given: mass of the body = m = 100 g = 0.1 kg, Radius of circular path = r = 2 m, Angular speed = ω = 7.5 rad/s,
To find: Linear speed = v =? Centripetal force = F = ?
Solution:
v = r ω = 2 x 7.5 = 15 m/s
F = m r ω2
∴ F = 0.1 x 2 x (7.5)2 = 11.25 N
Ans: Linear speed = 15 m/s, Centripetal force = 11.25 N radially inward.
Example – 24:
A car of mass 2000 kg rounds a curve of radius 250m at 90 km/hr. Compute its angular speed, centripetal acceleration and centrifugal force.
Given: Mass of car = m = 2000 kg, Radius of circular path = r = 250 m, Linear velocity of car = v = 90 km/hr = 90 x 5/18 = 25 m/s,
To find: Angular speed = ω =? centripetal acceleration = a = ?, centripetal force = F = ?,
Solution:
v = r ω
∴ ω = v/r = 25/250 = 0.1 rad/s
a = r ω2
∴ a = 250 x (0.1)2 = 2.5 m/s2
F = m a = 2000 x 2.5 = 5000 N radially inward
Ans: Angular speed = 0.1 rad/s, Centripetal acceleration = 2.5 m/s2 radially inward
The centripetal force and centrifugal force are equal in magnitude but opposite in direction.
Centrifugal force = 5000 N
Ans: Centrifugal force = 5000 N radially outward
Example – 25:
A 0.5 kg mass is tied to one end of a string and rotated in a horizontal circle of 1.25 m radius about the other end. What is the tension in the string if the period of revolution is 5 s. What is the maximum speed of rotation and the corresponding period if the string can withstand a maximum tension of 150 N.
Given: Mass of body = m = 0.5 kg, radius of curvature = r = 1.25 m, Period of revolution = T = 5 s,
To Find: Maximum speed of rotation = v =? F =? Part – II: Linear speed v =? when maximum tension = F = 150 N
Solution:
Part – I:
The necessary centripetal force acting on a body is given by tension in the string

Part – II:
The necessary centripetal force acting on a body is given by tension in the string

Ans: Tension in string = 0.986 N Maximum speed = 19.36 m/s. Period of revolution at maximum speed = 0.41 s
Example – 26:
A coin kept on a horizontal rotating disc has its centre at a distance of 0.1 m from the axis of rotation of the disc. If the coefficient of friction between the coin and the disc is 0.25, find the speed of the disc at which the coin would be about to slip off.
Given: radius of circular path = r = 0.1 m, coefficient of friction = μ = 0.25, g = 9.8 m/s2
To find: Speed of disc = v =?
Solution:
Necessary centripetal force is provided by the friction between the disc and coin.

Ans: The speed of the disc = 0.495 m/s.
Example – 27:
A coin kept on a horizontal rotating disc has its centre at a distance of 0.25 m from the axis of rotation of the disc. If μ = 0.2, find the angular velocity of the disc at which the coin is about to slip off. (g = 9.8 m/s2)
Given: radius of circular path = r = 0.25 m, coefficient of friction = μ = 0.2, g = 9.8 m/s2
To find: Angular speed of disc = ω =?
Solution:
Necessary centripetal force is provided by the friction between the disc and coin.

Ans: The angular speed of the disc = 7.84 rad/s.
Example – 28:
A coin just remains on a disc rotating at 120 r.p.m. when kept at a distance of 1.5 cm from the axis of rotation. Find the coefficient of friction between the coin and the disc.
Given: Radius of circular path = r = 1.5 cm = 0.015 m, rpm = N = 120 r.p.m., g = 9.8 m/s2
To find: coefficient of friction = μ =?
Solution:
Necessary centripetal force is provided by the friction between the disc and coin.

Ans: Coefficient of friction = 0.2415
Example – 29:
A coin just remains on a disc rotating at a steady rate of 180 rev/min if kept at a distance of 2 cm from the axis of rotation. Find the coefficient of friction between the coin and the disc.
Given: Radius of circle = r = 2 cm = 0.02 m, rpm = N = 180 r.p.m., g = 9.8 m/s2
To find: coefficient of friction = μ =?
Solution:
Necessary centripetal force is provided by the friction between the disc and coin.

Ans: The coefficient of friction = 0.724
Example – 30:
A coin kept with its centre at a distance of 9 cm from the axis of rotation of a disc starts slipping off when the disc speed reaches 60 r.p.m. Up to what speed the coin will remain on the disc if its centre is 16 cm from the axis of rotation of the disc?
Given: Initial radius of circle = r1 = 9 cm, initial rpm = N1= 60 r.p.m., final radius of circle = r2 = 16 cm
To find: Final rpm = N2 =?
Solution:
Necessary centripetal force is provided by the friction between the disc and coin.

Ans: The required angular speed = 45 r.p.m.
Example – 31:
A coin placed on a turntable rotating at 30 r.p.m. revolves with the table without slipping provided it is not more than 12 cm away from the axis. How far from the axis can the coin be placed so that it revolves with the turntable without slipping if the speed of rotation is 45 r.p.m.?
Given: Initial radius of circle = r1 = 12 cm, initial rpm = N1= 45 r.p.m., Final rpm = N2 = 45 r.p.m.
To find: final radius of circle = r2 =?
Solution:
Necessary centripetal force is provided by the friction between the disc and coin.

Ans: The maximum displacement from centre = 5.33 cm.
Example – 32:
A coin is placed at a distance of 10 cm from the centre of a turntable of radius 1m just begins to slip, when the turntable rotates at a speed of 90 r.p.m. Calculate the coefficient of static friction between the coin and the turntable.
Given: Radius of circle = r = 10 cm = 0.1 m, speed of rotation = N = 90 r.p.m.
To Find: Coefficient of Friction = m =?
Solution:
The necessary centripetal force is provided by the friction between the turntable and coin

Ans: The coefficient of friction is 0.9066
Example – 32:
With what maximum speed a car be safely driven along a curve of radius 40 m on a horizontal road if the coefficient of friction between the car tyres and the road surface is 0.3? (g = 9.8 m/s2)
Given: Radius of circular path = r = 40 m, coefficient of friction = μ = 0.3, g = 9.8 m/s2
To find: Maximum speed = v =?
Solution:
Necessary centripetal force is provided by the friction between the road and tyres.

Ans: The speed of the car = 10.84 m/s.
Example – 33:
Find the maximum speed at which a car can be safely driven along a curve of 100m radius. The coefficient of friction between tyres and the surface of the road is 0.2.
Given: radius of curve = r = 100 m, coefficient of friction = μ = 0.2, g = 9.8 m/s2
To find: maximum speed = v =?
Solution:
Necessary centripetal force is provided by the friction between the road and tyres.

Ans: The speed of the car = 14 m/s.
Example – 34:
A car travelling at 18 km/h just rounds a curve without skidding. If the road is plain and the coefficient of friction between the road surface and the tyres is 0.25, find the radius of the curve.
Given: Speed of car = v = 18 km/hr = 18 x 5/18 = 5 m/s, coefficient of friction = μ = 0.25, g = 9.8 m/s2
To find: radius of curve = r =?
Solution:
Necessary centripetal force is provided by the friction between the road and tyres.

Ans: The radius of road = 10.2 m.
Example – 35:
A car can just go around a curve of 20 m radius without skidding when travelling at 36 km/h. If the road is plain, find the coefficient of friction between the road surface and tyres.
Given: Speed of the car = v = 36 km/hr = 36 x 5/18 = 10 m/s, r = 20m, g = 9.8 m/s2
To find: coefficient of friction = μ =?
Solution:
Necessary centripetal force is provided by the friction between the road and tyres.

Ans: The coefficient of friction = 0.5102
Example – 04:
A flat curve highway has a radius of curvature 400 m. A car rounds the curve at a speed of 32 m/s. What is the minimum value of the coefficient of friction that will prevent the car from sliding?
Given: Radius of curvature = r = 400 m, speed of car = 32 m/s, g = 9.8 m/s2.
To Find: Coefficient of Friction = m =?
Solution:
The necessary centripetal force is provided by the friction between the road and tyres of the car

Ans: The coefficient of friction is 0.2612
Example – 36:
A rotor has a diameter of 4.0 m. The rotor is rotated about the central vertical axis. The occupant remains pinned against the wall. When the linear velocity of the drum is 8 m/s. Compute the coefficient of static friction between the wall of the rotor and the clothing of occupant. Also, calculate the angular velocity of the drum. How many revolutions will it make in a minute?
Given: diameter = d = 4 m, radius = r = 4/2 = 2 m, linear speed = v =.8 m/s , g = 9.8 m/s2 ,
To find: Coefficient of friction = μ = ?, Angular velocity = ω = ?, rpm = N = ?
Solution:

As the occupant remains pinned against the wall, his weight is equal to the frictional force.
Frictional force = Weight of a body


Ans: Coefficient of friction = 0.3063, Angular velocity = 4 rad/s, Number of revolutions per minute = 38.21.
Previous Topic: More Problems on Centripetal Force
Next Topic: Concept of Banking of Road