Science > Physics > Circular Motion > Centripetal Acceleration
In this article, we shall study the concept of centripetal acceleration and expression for it. Centripetal acceleration is also called radial acceleration.
Accelerated Motion:
Velocity is a vector quantity which has magnitude as well as direction. Either magnitude or direction or both change the motion is nonuniform motion
- Case – I: When direction remains the same, but magnitude changes e.g. Motion under gravity.
- Case – II: When magnitude remains the same, but the direction changes continuously e.g. Uniform circular motion:
- Case – III: When both the magnitude and direction changes continuously e.g. Projectile motion
The acceleration of the body performing circular motion which is directed towards the centre of the circular path along the radius is called a radial acceleration or centripetal acceleration.
Characteristics of Centripetal Acceleration:
- It is the acceleration of a particle performing the circular motion, which is directed towards the centre of the circular path along the radius.
- It is always directed towards the centre of the circular path along the radius.
- The direction of centripetal acceleration changes continuously.
- For U.C.M. the magnitude of the centripetal acceleration is constant.
- It is denoted by the letter ‘a’. Its S.I. unit is metre per square second (m s-2). Its dimensions are [MºL1T -2].
- The magnitude of centripetal acceleration is given by
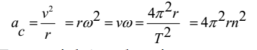
The Expression for Centripetal Acceleration
Geometric Method:
The magnitude of the velocity of a particle performing uniform circular motion is constant but its direction changes constantly. Hence the particle in circular motion has linear acceleration.
Let us consider a particle performing uniform circular motion with a linear velocity of magnitude ‘v’ and angular velocity of magnitude ‘ω’ along a circle of radius ‘r’ with centre O in an anticlockwise sense (moving from initial position A to final position B)as shown in the figure.
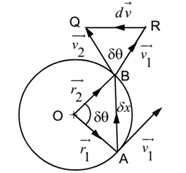
Triangle QBR is drawn for the velocities of the particles at A and B.

Now by definition,

The triangles AOB and RBQ are similar. Hence ∠ QBR = δθ
For smaller angular displacement δθ,

Substituting in equation (1), we get

This is the expression for the acceleration of particle performing the uniform circular motion.
This acceleration is directed towards the centre of the circular path along the radius. This acceleration is called radial acceleration or centripetal acceleration. In vector form, centripetal acceleration can be given as

The negative sign indicates that centripetal acceleration is oppositely directed to that of radius vector i.e. directed towards the centre of the circle along the radius.
Note: the alternate formula is

Centripetal acceleration is also called radial acceleration. It always acts along the radius towards the centre of the circular path. The angle between radius vector and centripetal acceleration is π radian or 180°.
Cartesian Method or Calculus Method:
Let us consider a particle performing uniform circular motion with a linear velocity of magnitude v and angular velocity of magnitude ω along a circle of radius r with centre O in an anticlockwise sense. Let the particle moves from A to P, in time ‘t’ Such that ∠ POA = θ.

But for uniform Circular motion θ = ω t. Thus, ∠ POA = ω t
Let us draw seg PM perpendicular to seg OA. Thus, ∠ POM = ω t
The radius vector at time t at P is given by

Substituting these values in equation (1)

The
linear velocity of a particle can be obtained by differentiating equation (2)
w.r.t. time t.

The linear acceleration of a particle can be obtained by differentiating equation (3) w.r.t. time t.

From equations (1) and (4) we have

Thus the magnitude of the acceleration is v2/r and its direction is along the radius and the negative sign indicates that it is opposite to the radius vector i.e. the acceleration is directed towards the centre of the circular path. This acceleration is called the centripetal acceleration.
Relation between linear velocity (v) and angular velocity (ω) by calculus method:
From the equation (3) we get the instantaneous velocity as

Thus the linear velocity of a particle performing U.C.M. is radius times its angular velocity.
Angle between linear velocity (v) and radius vector by calculus method:
From the equations (2) and (3) we have

Thus the scalar or dot product of the velocity of the particle performing U.C.M. and the radius vector is zero. Hence the angle between the velocity of the particle performing U.C.M. and the radius vector.
Acceleration of a Body Performing Circular Motion has Two Components:
The relation between linear velocity and angular velocity In vector form is written as

Thus the acceleration of the body performing circular motion has two components. one along the radius of the circular path towards the centre and is called centripetal acceleration and another tangential component. The net acceleration of the body is given by

Numerical Problems:
Example – 1:
The length of an hour hand of a wristwatch is 1.5 cm. Find the magnitudes of following w.r.t. tip of the hour hand a) angular velocity b) linear velocity c) angular acceleration d) radial acceleration e) tangential acceleration f) linear acceleration
Given: r = 1.5 cm = 1.5 x 10-2 m, For hour hand TH = 12 hr = 12 x 60 x 60 sec
To Find: Angular velocity = ω = ?, linear velocity = v = ?, angular acceleration = α = ?, radial acceleration = ar = ?, tangential acceleration = aT =?, linear acceleration a = ?
Solution:

Now v = r ω = 1.5 x 10-2 x 1.454 x 10-4 = 2.181 x 10-6 m/s
Tip of hour hand performs uniform circular motion
∴ α = 0 and aT = 0
Radial acceleration is given by

Now linear acceleration

Ans: Angular speed = 1.454x 10-4 rad/s, Linear speed =2.181 x 10-6 m/s,
Angular acceleration = 0, Radial acceleration = 3.171 x 10-10 m/s2.
Tangential acceleration = 0, Linear acceleartion = 3.171 x 10-10 m/s2.
Example – 2:
To simulate the acceleration of high-speed fighter plane, astronauts are spun at the end of a long rotating beam of radius 5 m. Find the angular velocity required to generate a centripetal acceleration 3 times the acceleration due to gravity.
Given: r = 5 m, a= 3g, g = 9.8 m/s2.
To find: ω =?
Solution:

Ans: Required angular velocity = 2.425 rad/s
Example – 3:
To simulate the acceleration of large rockets, astronauts are spun at the end of a long rotating beam of radius 9.8 m. Find the angular velocity required to generate a centripetal acceleration 8 times the acceleration due to gravity.
Given: r = 9.8 m, a= 8g, g = 9.8 m/s2.
To find: ω = ?
Solution:

Ans: Required angular velocity = 2.828 rad/s
Example – 4:
A body of mass 2 Kg is tied to the end of a string of length 1.5 m and revolved around the other end (kept fixed) in a horizontal circle. If it makes 300 rev/min, calculate the linear velocity, the acceleration and the force acting upon the body.
Given: m = 2 kg, r = 1.5 m, N = 300 r.p.m.,
To find: v = ?, a = ?, F = ?
Solution:

Centripetal force F = ma = 2 x 1479 = 2958 N
Ans: Linear speed of body = 47.13 m/s, Acceleration of body = 1480 m/s2,
Force acting on body = 2958 N radially inward.
Example – 5:
The tangential acceleration of a body performing circular motion is 29.48 m/s2 and its linear acceleration is 52.3 m/s2. Find its radial acceleration
Given: aT = 29.48 m/s2 and a = 52.3 m/s2.
To Find: ar =?
Solution:

Ans: The radial acceleration is 43.1 m/s2
Example – 6:
A particle is revolving in a circle. Its angular speed increases from 2 rad/s to 40 rad/s in 19 s. The radius of a circle is 20 cm. Compare the ratios of centripetal acceleration to tangential acceleration, at end of 19s.
Given: ω1 = 2 rad/s, ω2 = 40 rad/s, t = 38 s, r = 20 cm = 0.2 m.
To Find: ar : at =?
Solution:

Now at = r a = 0.2 x 2 = 0.4 m/s2
Centripetal acceleration at end of 19 s
Ar = r ω 2 = 0.2 x (40)2 = 320 m/s2
Ans: the required ratio ar : at =320: 0.4 = 800:1
Previous Topic: Numerical Problems on Circular Motion
Next Topic: Concept of Centripetal and Centrifugal Force