Science > Physics > Circular Motion > Numerical Problems on Centripetal Force – 01
Example – 01:
A 0.5 kg mass is rotated in a horizontal circle of radius 20 cm. Calculate the centripetal force acting on it, if its angular speed of revolution is 0.8 rad /s.
Given: Mass of a body = m = 0.5 kg, radius of circular path = r = 20cm = 0.2 m, Angular speed = ω = 0.8 rad/s,
To find: Centripetal force = F =?
Solution:
F = m r ω2
∴ F = 0.5 x 0.2 x (0.8)2
∴ F = 0.5 x 0.2 x (0.64) = 0.064 N
Ans: Centripetal force = 0.064 N acting radially inward.
Example – 02:
An object of mass 0.5 kg is whirled in a horizontal circle of radius 20 cm. Calculate centripetal force acting on it, if its angular speed of revolution is 0.6 rad/s.
Given: Mass of a body = m = 0.5 kg, radius of circular path = r = 20cm = 0.2 m, Angular speed = ω = 0.6 rad/s,
To find: Centripetal force = F =?
Solution:
F = m r ω2
∴ F = 0.5 x 0.2 x (0.6)2
∴ F = 0.5 x 0.2 x (0.36) = 0.036 N
Ans: Centripetal force = 0.036 N acting radially inward.
Example – 03:
A one kg mass tied at the end of the string 0. 5 m long is whirled in a horizontal circle, the other end of the string being fixed. The breaking tension in the string is 50 N. Find the greatest speed that can be given to the mass.
Given: Mass of a body = m = 1 kg, radius of circular path = r = 0.5 m, Centripetal force = F = 50 N.
To find: Greatest speed = v =?
Solution:
The necessary centripetal force acting on a body is given by tension in the string
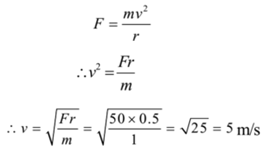
Ans: The greatest speed can be given to mass = 5 m/s
Example – 04:
2 kg mass is tied to a string at one end and rotated in a horizontal circle of radius 0.8 m about the other end. If the breaking tension in the string is 250 N, find the maximum speed at which mass can be rotated.
Given: Mass of a body = m = 2 kg, radius of circular path = r = 0.8 m, Centripetal force = F = 250 N.
To find: Maximum speed = v =?
Solution:
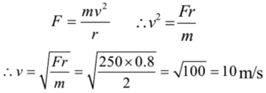
Ans: The greatest speed can be given to mass =10 m/s
Example – 05:
An object of mass 0.5 kg is whirled in a horizontal circle of radius 20 cm. Calculate the maximum number of revolutions per minute, so that the string does not break. The breaking tension of the string is 9.86 N.
Given: Mass of a body = m = 0.5 kg, radius of circular path = r = 20 cm = 0.2 m, Centripetal force = F = 9.86 N.
To find: Maximum rpm = N =?
Solution:
The necessary centripetal force acting on a body is given by tension in the string

Ans: Max. No. of revolutions = 94.87 r.p.m.
Example – 06:
A mass of 5 kg is tied at the end of the string 1.2 m long rotates in a horizontal circle. If the breaking tension in the string is 300 N, find the maximum number of rotations per minute the mass can make.
Given: Mass of a body = m = 5 kg, radius of circular path = r = 1.2 m, Centripetal force = F = 300 N.
To find: Maximum rpm = N =?
Solution:
The necessary centripetal force acting on a body is given by tension in the string

Ans: Max. No. of revolutions per minute = 67.56
Example – 07:
A stone is tied to a string 50 cm long and rotated uniformly in a horizontal circle about the other end. If the string can support a maximum tension ten times the weight of the stone, find the maximum number of revolutions per second the string can make before it breaks.
Given: Mass of a body = m, radius of circular path = r = 50 cm = 0.5 m, Centripetal force = 10 mg.
To find: Maximum number of revolutions per second = n =?
Solution:
The necessary centripetal force acting on a body is given by tension in the string

Ans: Max. No. of revolutions per second = 2.23
Example – 08:
A certain string breaks under a tension of 45 kg-wt. A mass of 100 g is attached to one end of a piece of this string 500 cm long and rotated in a horizontal circle. Neglecting the effect of gravity, find the greatest number of revolutions which, the sting can make without breaking.
Solution:
Given: Mass of a body = m = 100g = 0.1 kg, radius of circular path = r = 500 cm = 5 m, Centripetal force = F = 9.86 N.
To find: Maximum rps = n =?,
The necessary centripetal force acting on a body is given by tension in the string

Ans: Max. No. of revolutions per second = 4.73
Example – 09:
The breaking tension of a string is 80 kg.-wt. A mass of 1 kg is attached to the string and rotated in a horizontal circle on a horizontal surface of radius 2 m. Find the maximum number of revolutions made without breaking.
Given: Mass of a body = m = 1 kg, radius of circular path = r = 2 m, Centripetal force = F = 80 kg wt = 80 x 9.8 N.
To find: Maximum rps = n =?
Solution:
The necessary centripetal force acting on a body is given by tension in the string

Ans: Max. No. of revolutions per second = 3.15
Example – 10:
A string breaks under a tension of 10 kg-wt. If a string is used to revolve a body of mass 1.2 g in a horizontal circle of radius 50 cm, what is the maximum speed with which a body can be resolved? When a body is revolving at maximum speed, what is its period? (g = 9.8 m/s2)
Given: Mass of a body = m = 1.2 g = 1.2 x 10-3 kg, radius of circular path = r = 50 cm = 0.5 m, Centripetal force = F = 10 kg wt = 10 x 9.8 N.
To find: Maximum speed = v =? Period = T = ?
Solution:
The necessary centripetal force acting on a body is given by tension in the string

Ans: Max. Speed = 202.1 m/s, Period of revolution at maximum speed = 0.016 s
Example – 11:
A spherical body of mass 1 kg and diameter 2 cm rotates in a horizontal circle at the end of a string 1.99 m. long. What is the tension in the string when the speed of rotation is 6 revolutions in 1.5 s?
Given: Mass of the body = m = 1 kg, diameter of sphere = d = 2cm = 0.02 m. Radius of sphere = 0.01 m, radius of circular path = r = 1.99 + 0.01 = 2m, No. of revolutions = 6, time taken t = 1.5 s.
To find: Tension in string = F =?
Solution:

The necessary centripetal force acting on a body is given by tension in the string
n = 6/1.5 = 4 rad/s
ω = 2πn = 2 x 3.14 x 4 = 25.12 rad/s
F = m r ω2
∴ F = 1 x 2 x (25.12)2 = 1262 N
Ans: The tension in the string = 1262 N radially inward.
Example – 12:
A spherical bob of diameter 3 cm having a mass 100 g is attached to the end of a string of length 48.5 cm. Find the angular velocity and the tension in the string, if the bob is rotated at a speed of 600 r.p.m. in a horizontal circle. If the same bob is now whirled in a vertical circle of the same radius, what will be the difference in the tensions at the lowest point and the highest point?
Given: Mass of bob = m = 100 g = 0.1 kg, Radius of circular path = r = 48.5 cm + 1.5 cm = 50 cm = 0.5 m, rpm = N = 600 r.p.m.,
To Find: Angular velocity = ω=? Tension in the string = F = ?
Solution:
The necessary centripetal force acting on a body is given by tension in the string


The difference in the tensions at the lowest point and the highest point
= 6mg = 6 x 0.1 x 9.8 = 5.88 N
Ans: Angular speed = 62.84 rad/s, The tension in string =.197.2 N, The difference in the tensions at the lowest point and the highest point is 5.88 N
Example – 13:
A body of mass 2 Kg is tied to the end of a string of length 1.5 m and revolved about the other end (kept fixed) in a horizontal circle. If it makes 300 rev/min, calculate the linear velocity, the acceleration and the force acting upon the body.
Given: Mass of the body = m = 2 kg, radius of circular path = r = 1.5 m, Revolutions per minute = N = 300 r.p.m.,
To find: Linear speed = v =? Acceleration = a = ?, Force = F = ?
Solution:
The necessary centripetal force acting on a body is given by tension in the string

Ans: Linear speed of body = 47.13 m/s; acceleration of body = 1480 m/s2; Force acting on body = 2958N radially inward
Example – 14:
A body of mass 20 g rests on a smooth horizontal plane. The body is tied by a light inextensible string 80 cm long to a fixed point in the plane. Find the tension in the string if the body is rotated in a circular path at 30 rev/min. What is the force experienced by a fixed point?
Given: Mass of the body = m = 20 g = 0.020 kg, radius of circular path = r = 80 cm = 0.8 m, rpm = N = 30 r.p.m.,
To find: Tension in string = F =?
Solution:
The necessary centripetal force acting on a body is given by tension in the string

Ans: Tension in the string = 0158 N radially inward. The fixed point experiences a force of 0.158 N Radially outward.
Example – 15:
How fast should the earth rotate about it axis so that the apparent weight of a body at the equator be zero? How long would a day be then? Take the radius of the earth = 6400 km.
Given: Radius of earth = R = 6400 km = = 6.4 x 106 m.,
To find: Angular speed of earth = ω =?, period of earth = T = ?
Solution:
As the apparent weight of the body is zero. The centrifugal force and the weight of the body are equal in magnitude. Let m be the mass of the body.

Ans: The angular speed of earth then = 1.24 x 10-3 rad/s
T = 2π/ ω = (2 x 3.142)/( 1.24 x 10-3) = 5077 s
Ans: The duration of the day then = 5077 s
Example – 02:
An object of mass 100 g moves around the circumference of a circle of radius 2m with a constant angular speed of 7.5 rad/s. Compute its linear speed and force directed towards centre.
Solution:
Given: mass of thre body = m = 100 g = 0.1 kg, Radius of circular path = r = 2 m, Angulae speed = ω = 7.5 rad/s,
To find: Linear speed = v = ?, Centripetal force = F = ?
v = r ω = 2 x 7.5 = 15 m/s
F = m r ω2
∴ F = 0.1 x 2 x (7.5)2 = 11.25 N
Ans: Linear speed = 15 m/s, Centripetal force = 11.25 N radially inward.
Example – 16:
An electron of mass 9 x 10-31 kg is revolving in a stable orbit of radius 5.37 x 10-11 m. If the electrostatic force of attraction between electron and proton is 8 x 10-8 N. Find the velocity of the electron.
Given: Mass of electron = m = 9 x 10-31 kg, r = 5.37 x 10-11 m, F = 8 x 10-8 N
To find: velocity of electron = v =?
Solution:
The necessary centripetal force is given by electrostatic attraction between an electron and a proton.

Ans: The velocity of the electron is 2.185 x 106 m/s
Example – 17:
A bucket containing water is tied to one end of a rope 8 m long and rotated about the other end in a vertical circle. Find the minimum number of rotations per minute in order that water in the bucket may not spill? (g = 9.8 m/s2)
Given: Radius of circular path = r = 8 m, g = 9.8 m/s2,
To find: rpm = N =?
Solution:
At the highest point, the centrifugal force and the weight of water and bucket are equal in magnitude. Let m be the mass of the water and bucket.
mg = m r ω2
∴ g = r ω2
∴ ω2 = g /r = 9.8/8 = 1.225
∴ ω= 1.107 rad/s
ω= 2πN / 60
∴ N = 60ω/2π = (60 x 1.107) / (2 x 3.142) = 10.57
Ans: Max. No. of revolutions per minute = 10.57
Example – 18:
A bucket containing water is tied to one end of a rope 0.75 m long and rotated about the other end in a vertical circle. Find the speed in order that water in the bucket may not spill? Also, find the angular speed. (g = 9.8 m/s2)
Given: Radius of circle = r = 0.75 m, g = 9.8 m/s2
To find: linear speed = v =? angular speed = ω= ?
Solution:
At the highest point, the centrifugal force and the weight of water and bucket are equal in magnitude.
Let m be the mass of the water and bucket.

Ans: The linear velocity of bucket = 2.711 m/s, Angular speed of bucket = 3.615 rad/s
Previous Topic: Theory of Centripetal Force and Centrifugal Force
Next Topic: More Problems on Centripetal Force