Centripetal and Centrifugal Force

Science > Physics > Circular Motion > Centripetal and Centrifugal Force

In this article, we shall study the concept of centripetal force and centrifugal force, their expressions, and examples.

Centripetal Force:

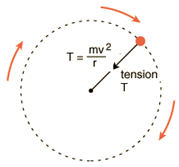
A force which acts on a body performing circular motion and acts along the radius of the circular path and directed towards the centre of the path is called centripetal force.

Example: When a stone tied to one end of a string is whirled horizontally in a circle, there is an inward force exerted by the string on the stone called tension. The tension in the string provides necessary centripetal force for circular motion.

Without centripetal force, circular motion is not possible. If centripetal force vanishes at some instant, then the body ceases to move in the circular path and flies along the tangent at that point to the circular path.

On the surface of the earth, the centripetal force is maximum at the equator and zero on the poles.

Expression For Centripetal Force:

If ‘m’ is the mass of the particle performing circular motion then the magnitude of the centripetal force is given by

Centripetal force = mass  x  centripetal acceleration.

It is a vector quantity and always directed towards the centre of the circle. In vector form

Characteristics of Centripetal Force:

• It is a real force because it is provided by gravitational, electromagnetic or nuclear interaction.
• It arises in an inertial frame of reference. The inertial reference frame is that frame of reference which is moving with uniform velocity w.r.t. earth.
• It is always directed towards the centre of the circular path.
• Without it, the circular motion is not possible.
• The work done by the centripetal force is zero because the displacement of the particle (tangential) is perpendicular to the direction of the centripetal force (radial) i.e. there is no displacement in the direction of the centripetal force.
• The torque produced by the centripetal force at the center of the circular path is zero.
• The direction of the centripetal force does not depend on the sense of rotation of the body.

Notes:

The kinetic energy of a body performing a circular motion in terms of centripetal force is

K.E. = F.r/2

The linear momentum of a body performing a circular motion in terms of centripetal force is

p = F.r / v

Change in the velocity of a body performing U.C.M. and when it moves through angle θ is

dv = 2 sin(θ/2)

Examples of Centripetal Force:

• When a stone tied to one end of a string is whirled horizontally, there is an inward force exerted by the string on the stone called tension. This force provides necessary centripetal force for circular motion.

• Satellite revolves around the earth in a circular orbit. Necessary centripetal force is provided by the gravitational force of attraction between satellite and earth.

• When a vehicle moves around a horizontal circular road, the centripetal force for circular motion is provided by the frictional force between the road and the wheels.

• In an atom, an electron moves around the nucleus in an orbit. The centripetal force required for the motion of the electron is provided by the electrostatic force of attraction between the negatively charged electron and positively protons.

• When a coin is kept on rotating disc necessary centripetal force is provided by friction between the coin and the surface of the rotating disc.

• In a circus, when the motorcyclist moves in a vertical circle in the sphere of death, at the highest point of the vertical circle, the necessary centripetal force is provided by the weight of the motorcycle and motorcyclist.

• When a body is performing looping a loop, at the highest point of the vertical circle, the necessary centripetal force is provided by the weight of the body. For looping a loop the speed of motorcyclist at the lowest point should be greater than √5gr  and at the highest point, the speed should be greater than √gr.

Centrifugal Force:

The imaginary force which acts on the particle performing a circular motion in the direction away from the centre along the radius of the circular path having the same magnitude as that of centripetal force is called centrifugal force.

Example: When moving a car takes a turn along a horizontal curved road, persons in the car experience a force in the outward direction. This force is centrifugal force

It has the same magnitude and opposite direction to that of centripetal force.

It should be noted that the centrifugal force is not real force’ since it does not arise due to either gravitational or electrostatic or nuclear interaction.

Centrifugal Force is a Pseudo Force:

• Centrifugal force is not real force since it does not arise due to either gravitational or electrostatic or nuclear interaction.
• Centrifugal force has no independent existence. It comes to play with the action of the centripetal force. It does not arise due to either gravitational or electrostatic or nuclear interaction.
• Centrifugal force acts in the non-inertial reference frame
  Hence centripetal force is a pseudo force.

Theoretical Explanation:

Case – I:

Let us consider body P is tied to a string and lying on a frictionless turntable and performing uniform circular motion along with turntable in a clockwise sense as shown. The necessary centripetal force is provided by the tension in the string. Let A be an observer standing between the centre of the table and the particle at P. Let P₁, P₂, P₃ be different positions of the particle on the circular path. Let A₁, A₂, A₃ be corresponding positions of observer A. Observer B is standing near table B outside the turntable. As observer B is stationary w.r.t. the earth he is an inertial frame of reference, while observer A is acted upon by centripetal acceleration. Thus observer A is in acceleration w.r.t. earth, observer A is a non-inertial frame of reference.

Let us check the opinion of observer B about the motion of particle P. His observation is that he is stationary and the particle P is in a circular motion and a centripetal force acts on it. The necessary centripetal force is provided by the tension in the string. There is a centripetal acceleration and is provided by centripetal force. Thus his observations by B are in accordance with Newton’s laws of motion.

Now let us check observation of observer A. He says that he is stationary and every instant particle is in front of me at a constant distance, hence particle is stationary. There is tension in the string. Thus force is acting on particle directed towards centre but particle is stationary. By Newton’s second law is F = ma. Thus if there is a force, the state of motion of the body should change. But as per observer A, the state of motion of the body is not changing in spite of the action of the force. Thus Newton’s second law of motion fails. To correct A we have to assume some imaginary force (centrifugal force) which is equal to the tension in the string acts radially outward i.e. opposite and equal to centripetal force. Under the action of these equal and opposite forces acting on the body, the body does not change its change of state of motion.

We can see that the concept of centrifugal force (imaginary) is not required by B but is required by observer A who is the noninertial frame of reference.

Case- II:

Now let us assume the string breaks when the particle is at position P₁. The particle is thrown off with uniform velocity along the tangent to the circular path at position P₁.

Let us check the new opinion of observer B about the motion of particle P. His observation is that I am he is stationary and the body is moving along a straight line with uniform velocity and no force acts on it. It is in accordance with Newton’s first law of motion.

Now let us check new observation of observer A. He says that he is stationary and the body P moves outward with constant acceleration but no force acts on it. Thus Newton’s second law of motion fails. To correct A we have to assume some imaginary force (centrifugal force) which is equal to the tension in the string acts radially outward. Under the action of this force, the body moves radially outward with acceleration.

Thus in both the case we have to assume the existence of imaginary or pseudo force to correct observer A, which is non-inertial reference frame..

Centripetal Force and Centrifugal Force Do Not Constitute Action-Reaction Pair:

A statement ” A particle moving uniformly along a circle experiences a force directed towards the centre (centripetal force) and an equal and opposite force directed away from the centre (centrifugal force). The two forces keep the particle in equilibrium” is completely wrong.

Because the particle in a circular motion is not in equilibrium because a net force (centripetal force) acts towards the centre which is required to change the direction of particle continuously. Centripetal force is a real force.

The centrifugal force is an imaginary force is required by an observer moving with the particle. The observer is a non-inertial reference frame and for the observer, the particle is at rest.

Centripetal force is required for circular motion. Centrifugal force does not have an independent existence. It comes into play when the centripetal force starts acting. Thus the centripetal force and centrifugal force do not constitute the action-reaction pair.

Characteristics of Centrifugal Force:

• It is an imaginary force or pseudo force.
• It is experienced in non – inertial frame of reference.
• The magnitude of the centripetal force is equal to that of the centripetal force.
• It is always directed away from the centre of the circle along the radius
• it is directed opposite to the centripetal force.
• Centrifugal force doesn’t have an independent existence.

Examples of Centrifugal Force:

• When a moving car along a horizontal curved road takes a turn, persons in the car experience a force in an outward direction. This force is centrifugal force.

• When the horizontal merry go round rotates about the vertical axis the chairs are pulled out due to centrifugal force.

• When a stone is whirled in a circle, we feel that stone is pulling our hand because of centrifugal force.

• The earth is flattened at the poles and bulged at the equator because the centrifugal force acting on the particles on the equator is maximum.

• The drier of a washing machine acts on the principle of centrifugal force. Water particles from wet clothes are thrown outward due to centrifugal force acting on them. Drier in the washing machine consists of a cylindrical vessel with perforated walls. As the cylindrical vessel is rotated fast, centrifugal force acts on the water particles of wet clothes. Under the action of this centrifugal force, water particles are forced out of the perforations, thereby drying of the clothes.

• When a pilot moves the plane in looping a loop, he does not fall down because his weight is balanced by the centrifugal force acting on it.

• A coin kept slightly away from the center of rotating gramophone disc slips off towards the edge of the disc at a particular speed. This is due to centrifugal force acting on the coin.

• A bucket full of water is rotated in a vertical circle at a particular speed, so that water does not fall. This is because the weight of the water is balanced by centrifugal force.

• The centrifuge is a device which is used for separating heavier particles and light particles and works on the principle of centrifugal force. In the centrifuge, the tube containing liquid along with the suspended particles is whirled in a horizontal circle. Dense particles are acted upon by a centrifugal force. Hence they get accumulated at the bottom, which is outside while rotating. This is because buoyant force towards the center is greater for the lighter particle.

• Centrifugal governor works on the principle of centrifugal force. When the speed of the vehicle increases beyond a certain set limit, the fly balls under the action of centrifugal force, fly away from the axis of rotation. A bell and crank arrangement attached to it reduces the flow of fuel to the engine. Thus the speed of the vehicle is governed.

• Centrifugal pump works on this principle. It sucks water through a pipe from the reservoir and throws outward under the action of centrifugal action in the involute casing and thus produces a draft and water is lifted up.

• When wheels are rotating mud stuck to the wheels and then under the action of centrifugal force are thrown tangentially away from the wheels. These mud particles tarnish the vehicle and spray the mud on the following vehicles. At the same time, these mud article may degrade the performance of the brake. When mudguards are used the mud particles are stopped dead and fall down under gravity.

Distinguishing Between Centripetal Force and Centrifugal Force:

Centripetal Force	Centrifugal Force
Centripetal force is a force which is acting on a body performing circular motion and is acting along the radius of the circular path and directed towards the centre of the circle.	The imaginary (pseudo) force which acts on the particle performing a circular motion in the direction away from the centre along the radius of the circular path having the same magnitude as that of centripetal force is called as centrifugal force.
It is a real force.	It is an imaginary force or a pseudo force.
It arises in an inertial frame of reference.	It is experienced in non – inertial frame of reference.
It is always directed towards the centre of the circular path.	It is always directed away from the centre of the circle along the radius.
Without it, the circular motion is not possible.	Centrifugal force doesn’t have an independent existence.
Example: The moon or a Satellite revolves around the earth in circular orbit. Necessary centripetal force is provided by the gravitational force of attraction between satellite and earth.	Example: When moving car takes a turn along a horizontal curved road, persons in the car experience a force in the outward direction. This force is centrifugal force

Previous Topic: Concept of Centripetal Acceleration

Next Topic: Numerical Problems on Centripetal Force

Science > Physics > Circular Motion > Centripetal and Centrifugal Force