Science > Physics > Force > Applications of Newton’s Laws
Newton’s laws of motion have everyday applications. The change in momentum of a body in a small time is a cause of large force. Most of the applications are related to the concept of change in momentum.
Cricket fielder lowers his hand while catching a ball:
If the ball is caught without lowering hands, the duration of the impact is small. As a result, the rate of change of momentum increases producing a large force. Thus the fielder will hurt his hands due to large force. When the ball is caught by moving the hand in the direction of the motion of the ball, the duration of impact increases. As a result, the rate of change of momentum decreases and thus the force exerted by the ball on hands get reduced.
An athlete taking a long jump or a high jump bends his knees before landing:
If the athlete does not bend his knees before landing, the duration of the impact is small. As a result, the rate of change of momentum increases producing a large force. Thus the athlete will hurt his legs due to large force. If the athlete bends his knees before landing, the duration of impact increases. As a result, the rate of change of momentum decreases and thus the force exerted by the ground (Reaction) on the athlete get reduced. Thus the athlete lands safely by bending knees before landing.
A Blacksmith holds the rod on the anvil with his tongs while striking with his hammer:
For reshaping of a rod, the blacksmith has to apply very large force. By holding the rod on the anvil with his tongs while striking with his hammer, the blacksmith reduces the time of impact. As a result, the rate of change of momentum increases drastically producing a very large force.
An athlete runs a certain distance before taking a large jump:
Here Newton’s First law, second law, and Third law is used. As the athlete is running a certain distance he gets additional velocity and hence additional kinetic energy, when he is actually jumping. Due to high velocity at a point where he starts his jump (Point of rising) the time of impact is reduced. As a result the rate of change of momentum increases, producing a very large force on the ground. The ground produces a large reaction and thus a long jump can be taken easily.
A clean hole is made in a glass windowpane when it is struck by a bullet fired from a gun. Whereas the same windowpane will be broken into pieces when struck by a stone of similar size:
When a bullet is fired at a glass window, a clear hole is formed in it. This is because only that part of the glass moves with the bullet, where the bullet hits the glass. The remaining part due to the inertia remains in its position. Thus bullet is able to form a hole in the glass window due to the inertia of window pane. The time for which the force is applied is very small, thus there is very less time for the reaction by the window pane.
When the same window pane is struck with a stone of a similar size, the time for which the force is applied is large compared to that in case of a fired bullet. Thus all the section around the striking point is set into motion. Due to the brittle nature of the glass, this impact causes it to break into pieces.
The engine of a moving car exerts a constant force on the car, but car movers with a constant velocity:
When a car is moving there is friction between different parts of the engine and mechanisms, besides there is friction between the road and the tyres. These frictional forces are opposed to the direction of motion. In the case of a car moving with a constant velocity the forward force exerted by the engine on the car is exactly equal and opposite to the car backward force exerted on the car due to friction and resultant force acting on the car is zero. This is the reason why the case moves with a constant velocity, even though the engine exerts a force on the car.
Apparent Weight of a Person in a Lift:
Let a person of mass ‘m’ standing on a weighing machine placed on the floor of the lift. The actual weight of the person is ‘mg’ which acts vertically down. The reaction offered by the weighing machine is ‘R’ which is also known as the apparent weight of the person.
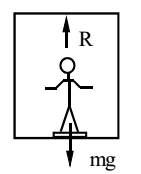
Case – 1 (When the lift is at rest):
Since the lift is at rest, the net force acting on the person is zero.
R – mg = 0. Thus R = mg.
Thus his apparent weight is equal to his actual weight.
Case – 2 (When the lift moves upward or downward with uniform velocity):
Since lift is moving with uniform velocity, the net acceleration of the lift is zero, thus the net force acting on the person is zero.
R – mg = 0. Thus R = mg.
Thus his apparent weight is equal to his actual weight.
Case – 3 (When the lift moves upward with constant acceleration):
As the lift is moving upward with the acceleration say ‘a’, the net force acting on the person is ‘ma’ acting upward.
R – mg = ma.
Thus R = mg + ma = m(g + a).
Thus his apparent weight is greater than his actual weight.
Case – 4 (When the lift moves downward with constant acceleration):
As the lift is moving downward with the acceleration, the net force acting on the person is ‘ma’ acting downward.
R – mg = – ma.
Thus R = mg – ma = m(g – a).
Thus his apparent weight is less than his actual weight.
Case – 5 (If the lift falls freely):
As the lift falls freely, its acceleration is equal to the acceleration due to gravity. Thus a = g. Substituting this value in equation of case -4 we get
R = m(g – g) = m(0) = 0.
Thus his apparent weight is zero and the person feels weightless. In this case, the surface on which the person is standing and the person himself have the same acceleration and the same direction of acceleration. Hence the person feels weightless.
In satellite orbiting around the earth, the astronaut and the surface of the spacecraft have the same acceleration acting towards the centre of the Earth. Hence the astronaut feels weightless.
Weightlessness is feeling and not actually weightless. The feeling of weightlessness can be experienced by a person jumping from a height.
Previous Topic: Newton’s Third Law of Motion
Next Topic: Simple Numerical Problems on Force