Introduction to Circular Motion

Science > Physics > Circular Motion > Introduction

Concept of Circular Motion:

The motion of a particle along the circumference of a circle is called circular motion. It is a translational motion along a curved path.

Examples:

• The motion of the earth around the sun.
• The motion of a satellite around the planet.
• The motion of an electron around the nucleus.
• The motion of a tip of a blade of a fan. (Note it is the motion of the tip of a blade of the fan and not the motion of the fan. The motion of fan is a rotational motion)

Characteristics of Circular Motion:

• In a circular motion, the particle moves along the circumference of a circle.
• It is a translational motion along a curved path.
• The magnitude of the radius vector or position vector is constant and equals to the radius of the circular path.
• The direction of the radius vector or position vector changes continuously.
• If the magnitude of the velocity (speed) of the particle performing constant, the particle is said to perform the uniform circular motion.
• If the magnitude of the velocity (speed) of the particle performing changes continuously, the particle is said to perform the non- uniform circular motion.

Radius Vector:

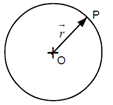
A vector drawn from the centre of a circular path to the position of the particle at any instant is called a radius vector at that instant. It is also called as a position vector. In the figure at position P,  r or OP is a position vector. The magnitude of the position vector is equal to the radius of the circular path. Hence for a circular motion, the magnitude of the radius vector is constant but its direction changes continuously.

Characteristics of Radius or Position Vector:

• It is always directed along the radius of the circular path.
• Its direction is from the centre of the circular path to the position of the particle at that instant i.e. is directed radially outward.
• In a circular motion, the magnitude of the radius vector or position vector is constant and equals to the radius of the circular path.
• The direction of the radius vector or position vector in circular motion changes continuously.
• Its direction is opposite to that of centripetal acceleration and the centripetal force.
• It is denoted by r. Its dimensions are [MºL¹Tº]. Its S.I. unit is metre (m) and c.g.s. unit is centimetre (cm).

Instantaneous Velocity (v):

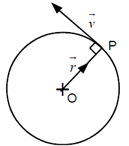
A linear velocity of a particle performing a circular motion, which is directed along the tangent to the circular path at a given point on the circular path at that instant is called instantaneous velocity. It is also called as tangential velocity.

For uniform circular motion the magnitude of instantaneous velocity is always constant but direction changes continuously. For non-uniform circular motion, the magnitude and direction of the instantaneous velocity change continuously.

The tangential velocity is directed perpendicular to the direction of the radius vector.

If a stone is tied to one end of a string and whirled in a horizontal circle at the other en, necessary centripetal force is provided by the tension in the string. If the speed of rotation is increased gradually, the tension in the string increases, a stage is reached when the tension in string becomes larger than the breaking tension of the string, the string breaks and the stone flies off tangentially.

Characteristics of Instantaneous Velocity or Tangential Velocity:

• It is always directed along the tangent to the circular path at a given point on the circular path at that instant.
• It is always perpendicular to the direction of the radius vector at the point represented by the radius vector on the circular path.
• For uniform circular motion the magnitude of instantaneous velocity is always constant but direction changes continuously.
• For non-uniform circular motion, the magnitude and direction of the instantaneous velocity change continuously.
• It is denoted by v. Its dimensions are  [MºL¹T^-1]. Its S.I. unit is metre per second  (m s^-1) and c.g.s. unit is centimetre per second (cm s^-1).

Axis of Rotation:

The normal drawn to the plane of the circular path through the centre of the circular path is called the axis of rotation.

Note: In rotational motion, the particles on the axis of rotation are stationary, while all other particles perform circular motion about the axis of rotation.

Uniform Circular Motion:

The motion of a particle along the circumference of a circle with a constant speed is called uniform circular motion (U.C.M.).

Examples: The motion of the earth around the sun, The motion of an electron around the nucleus.

Characteristics of Uniform Circular Motion:

• The magnitude of the velocity (speed) of the particle performing U.C.M. is constant.
• The magnitude of the instantaneous velocity of the particle performing U.C.M.  remains constant but its direction changes continuously. Hence U.C.M. is accelerated motion.
• It is a periodic motion with a definite period and frequency.
• in U.C.M., the magnitude of the centripetal force acting on the body is constant
• in U.C.M., the linear speed, angular speed, radial (centripetal) acceleration, kinetic energy, angular momentum and magnitude of the linear momentum of the body remain constant.
• in U.C.M., the angular acceleration, tangential acceleration is zero.

The Period of Revolution:

The time taken by a particle performing uniform circular motion to complete one revolution is called the period of revolution or periodic time or simply period (T).

It is denoted by ‘T’. The S. I. Unit of the period is second (s). Its dimensions are [MºLºT ¹].

Characteristics of Time Period of U.C.M.:

• The time taken by a particle performing uniform circular motion to complete one revolution is called the period of revolution or periodic time or simply period (T).
• For U.C.M. it is constant.
• It is denoted by ‘T’. The S. I. Unit of the period is second (s). Its dimensions are [MºLºT ¹].

The Frequency of Revolution:

The number of revolutions by the particle performing uniform circular motion in unit time is called as frequency (n) of revolution.

The frequency is denoted by letter ‘n’ or ‘f’. The S. I. Unit of frequency is hertz (Hz). Its dimensions are [MºLºT^-1].

In time T the particles complete one revolution. Thus the particle completes 1/T revolutions in unit time. Thus n = 1/T.

Characteristics of Frequency of U.C.M.:

• The number of revolutions by the particle performing uniform circular motion in unit time is called as frequency (n) of revolution.
• For U.C.M. it is constant.
• The frequency is denoted by letter ‘n’ or ‘f’. The S. I. Unit of frequency is hertz (Hz). Its dimensions are [MºLºT-1].
• In time T the particles complete one revolution. Thus the particle completes 1/T revolutions in unit time. Thus n = 1/T.

Next Topic: angular Displacement, Angular Velocity, and Angular Acceleration

Science > Physics > Circular Motion > Introduction