In this article we shall study to solve problems on calculation of viscous force, coefficient of viscosity, and velocity gradient.
Example 01:
Calculate the horizontal force required to move a metal plate of area 2 x 10-2 m2 with a velocity of 4.5 x 10-2 m s-1 when it rests on a layer of oil 1.5x 10-3 m thick. η = 2 Nsm-2.
Given: Area of plate = 2 x 10-2 m2, Thickness of layer= dy = 1.5 x 10-3 m, Velocity of the plate = dv = 4.5 x 10-2 m s-1, η = 2 Nsm-2.
To Find: Required force = F =?
Solution:
By Newton’s law of viscosity
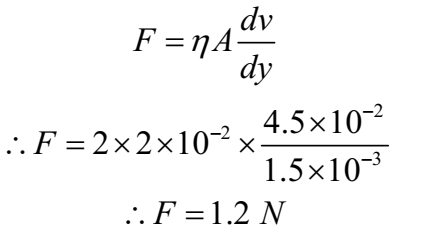
Ans: Required force is 1.2 N
Example 02:
A metal plate of area 25 x 10-3 rests on the surface of a viscosity liquid layer 2 mm thick. What horizontal force is needed to keep the plate moving with a constant speed of 2 cm s-1 if for the liquid is 1 S.I. unit?
Given: Area of plate = 25 x 10-3 m2, Thickness of layer= dy = 2 mm = 2 x 10-3 m, Velocity of the plate = dv = 2 cm s-1 = 2 x 10-2 m s-1, η = 1 SI unit.
To Find: Required force = F =?
Solution:
By Newton’s law of viscosity
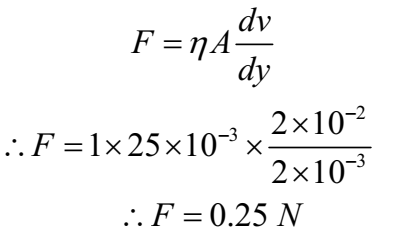
Ans: Required force is 0.25 N
Example 03:
There is 1 mm thick layer of glycerine between a flat plate of area 100 cm2 and a big plate placed parallel to it. If the coefficient of viscosity of glycerine is 1.0 kg m-1s-1, then how much force is required to move the late with a velocity of 7 cm s-1.
Given: Area of plate = 100 cm2 = 100 x 10-4 m2, Thickness o f layer= dy = 1 mm = 1 x 10-3 m, Velocity of the plate = dv = 7 cm s-1 = 7 x 10-2 m s-1, η = 1.0 kg m-1s-1=
To Find: Required force = F =?
Solution:
By Newton’s law of viscosity
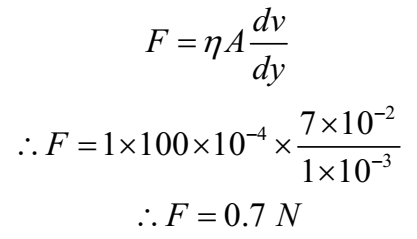
Ans: Required force is 0.7 N
Example 04:
A flat plate is separated from a large plate by a layer of glycerine of thickness 3 x 10-3 m. If the coefficient of viscosity of glycerine 2 Ns m-2 what is the force required to keep the plate moving with a velocity of 6 x 10-2 ms-1. Area of the plate is 4.8 x 10-3 m2.
Given: Area of plate = 4.8 x 10-3 m2, Thickness of layer= dy = 3 x 10-3 m, Velocity of the plate = dv = 6 x 10-2 m s-1, η = 2 Ns m-2.
To Find: Required force = F =?
Solution:
By Newton’s law of viscosity

Ans: Required force is 0.192 N
Example 05:
A metal plate 100 cm2 in area rests horizontally on a layer of oil 2 mm thick. A force of 0.1 N applied to the plane horizontally keeps it moving with a uniform speed of 2 cm/s. Find the viscosity of oil.
Given: Area of plate = 100 cm2 = 100 x 10-4 m2, Thickness of layer= dy = 2 mm = 2 x 10-3 m, Applied force = F = 0.1 N, Velocity of the plate = dv = 2 cm s-1 = 2 x 10-2 m s-1.
To Find: Viscosity of oil = η =?
Solution:
By Newton’s law of viscosity

Ans: Viscosity of oil is 1 pascal second
Example 06:
A metal plate 0.05 m2 in area rests horizontally on a layer of oil 1 μm = 1 x 10-6 m thick. A force of 20 N applied to the plane horizontally keeps it moving with a uniform speed of 10 cm/s. Find the viscosity of oil.
Given: Area of plate = 0.05 m2, Thickness of layer= dy = 1 μm = 1 x 10-6 m, Applied force = F = 20 N, Velocity of the plate = dv = 10 cm s-1 = 10 x 10-2 m s-1.
To Find: Viscosity of oil = η =?
Solution:
By Newton’s law of viscosity

Ans: Viscosity of oil is 1 pascal second
Example 07:
A metal plate of area 0.1 m2 is connected to 10 g mass via a string passing over weightless frictionless pulley as shown in the figure. A liquid with a film thickness of 0.3 mm is placed between the plate and the table. When released the plate moves to the right with constant speed of 8.5 cm s-1. Find the coefficient of viscosity of the liquid.

Given: Area of plate = 0.1 m2, Thickness of layer = dy = 0.3 mm = 0.3 x 10-3 m, Applied force = F = 10 g = 10 x10-3 x 9.8 N, Velocity of the plate = dv = 2 cm s-1 = 2 x 10-2 m s-1.
To Find: Viscosity of oil = η =?
Solution:
By Newton’s law of viscosity

Ans: Viscosity of oil is 3.46 x10-3 pascal second
Example 08:
A square plate of ide 20 cm moves parallel to another plate with a velocity of 20 cm s-1, both plates immersed in water. If the viscous force is 4 x 10-3 N and viscosity of water is 0.001 decapoise, what is their distance apart.
Given: Area of plate = 20 cm x 20 cm = 400 cm2 = 400 x 10-4 m2, Applied force = F = 4 x 10-3 N, Velocity of the plate = dv = 20 cm s-1 = 20 x 10-2 m s-1, Viscosity = η = 0.001 decapoise = 0.001 Ns m-2 (Note 1 decapoise = 1 Ns m-2)
To Find: Distance between layers = dy =?
Solution:
By Newton’s law of viscosity

Ans: The two plates are 2 mm apart.
Example 09:
A square plate of 0.1 m side moves parallel to another plate with a velocity of 0.1 ms-1, both plates immersed in water. If the viscous force is 0.02 N and the coefficient of viscosity 0.01 poise, what is the distance apart?.
Given: Area of plate = 0.1 m x 0.1 m = 0.01 m2, Applied force = F = 0.02 N, Velocity of the plate = dv = 0.1 m s-1, Viscosity = 0.01 poise = 0.001 decapoise = 0.001 Ns m-2
To Find: Distance between layer = dy =?
Solution:
By Newton’s law of viscosity

Ans: The two plates are 0.05 mm apart.
Example 10:
Two metal plates of area 2 x 10-4 each, are kept in water and one plate is moved over the other with certain velocity. The distance between the plates is 2 x 10-4 m. If the horizontal force applied to the moving plate is 10-3 N. Calculate the velocity of the plate. Given eta for water as 10-3 decapoise.
Given: Area of plate = 2 x 10-4 m2, Distance between plates = dy = 2 x 10-4 m, Applied force = F = 10-3 N, Viscosity = 0.01 poise = 10-3 decapoise = 10-3 Ns m-2
To Find: Velocity of plate = dv =?
Solution:

Ans: Velocity of plate is 1 ms-1.
Example 11:
The relative velocity between two layers of water is 8 cm s-1 and the distance between these two layers is 0.1 cm, find velocity gradient.
Given: Relative velocity between the plate = dv = 8 cm s-1 = 8 x 10-2 m s-1, Distance between layers = 0.1 cm = 0.1 x 10-2 m
To Find: Velocity gradient = dv/dy =?
Solution:
dv/dy = 8 x 10-2/ 0.1 x 10-2 = 80 s-1.
Ans: Velocity gradient is 80 s-1.