Composition of Two S.H.M.s

Science > Physics > Oscillations: Simple Harmonic Motion > Composition of Two SHM

In this article, we shall study the composition of two SHM. Sometimes particle is acted upon by two or more linear SHMs. In such a case, the resultant motion of the body depends on the periods, paths and the relative phase angles of the different SHMs to which it is subjected.

Consider two SHMs having same period and parallel to each other, where a1 and a2 are amplitudes of two SHMs respectively. a1 anda2 are initial phase angle of two SHMs respectively, whose displacements are given by

x₁ = a₁ Sin (ωt + α₁)   and x₂ = a₂ Sin (ωt + α₂)

Resultant displacement of the particle subjected to above SHMs is given by

x = x₁ + x₂

∴ x  = a₁ Sin (ωt + α₁)  +  a₂ Sin (ωt + α₂)

∴   x = a₁ [Sinωt . Cosα₁ + Cosωt . Sinα₁] + a₂ [Sinωt . Cosα₂ + Cosωt . Sinα₂]

∴   x = a₁ Sinωt . Cosα₁ + a₁ Cosωt . Sinα₁ + a₂ Sinωt . Cosα₂ + a₂ Cosωt . Sinα₂

∴   x = a₁ Sinωt . Cosα₁ + a₂ Sinωt . Cosα₂ + a₁ Cosωt . Sinα₁ + a₂ Cosωt . Sinα₂

∴   x = Sinωt .(a₁  Cosα₁  + a₂ Cosα₂) + Cosωt . (a₁ Sinα₁ + a₂  Sinα₂) ………….. (1)

Let, (a₁ Cosα₁  + a₂ Cosα₂)   = R Cos δ … (2)

(a₁ Sinα₁ + a₂ Sinα₂) = R Sin δ    ……(3)

From Equations (1), (2) and (3)

x = Sin ωt (R Cos δ)   + Cos ωt (R Sin δ)

∴   x = R (Sin ωt Cos δ   + Cos ωt Sin δ)

∴ x = R Sin (ωt + δ)  ………..(4)

Equation (4) indicates that resultant motion is also a S.H.M. along the same straight line as two parent SHMs and of the same period and initial phase δ .

Squaring equations (2) and (3) and adding them

(R Cos δ)²+    (R Sin δ)² =   (a₁  Cosα₁  + a₂ Cosα₂)² +   ( a₁ Sinα₁ + a₂  Sinα₂ )²

∴   R² Cos² δ+    R² Sin² δ =    a₁² Cos² α₁ + a₂² Cos² α₂ +2 a₁ a₂ Cos α₁ Cos α₂

+ a₁² Sin² α₁ + a₂²Sin²α₂ + 2 a₁ a₂ Sin α₁ Sin α₂

∴   R² (Cos² δ + Sin² δ) =    a₁² (Cos² α₁ + Sin² α₁) + a₂² (Cos² α₂ + Sin²α₂)

+2 a₁ a₂ (Cos α₁ Cos α₂ +Sin α₁ Sin α₂)

∴   R² (1) =    a₁² (1) + a₂² (1) +2 a₁ a₂ Cos (α₁ – α₂)

∴   R² =    a₁² + a₂² +2 a₁ a₂ Cos (α₁ – α₂)

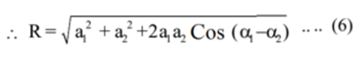
Dividing equation (3) by (2)

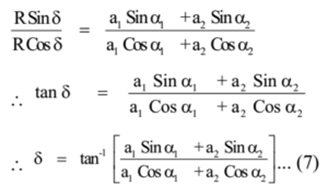
From Equations (6) and (7) we can find the resultant and initial phase of resultant S.H.M.

Special Cases:

Case 1: When the two SHMs are in the same phase then (α₁ – α₂) =  0

If the two SHMs have the same amplitude then, a₁ = a₂ = a

∴ R   =  a + a   =  2a

Case 2: When the two SHMs are in opposite phase then, (α₁ – α₂) = π

If the two SHMs have the same amplitudes then, a₁ = a₂ = a

R   = a – a = 0

Case 3: When the phase difference is (α₁ – α₂)   = π / 2

If the two SHMs have the same amplitude then, a₁ = a₂ = a

Previous Topic: Numerical Problems on Energy of Particle Performing S.H.M.

Next Topic: Theory of Simple Pendulum

Science > Physics > Oscillations: Simple Harmonic Motion > Composition of Two SHM