Conical Pendulum

Science > Physics > Circular Motion > Conical Pendulum

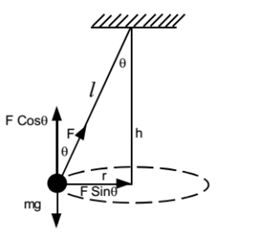
A conical pendulum consists of a bob of mass ‘m’ revolving in a horizontal circle with constant speed ‘v’ at the end of a string of length ‘l’. In this case, the string makes a constant angle with the vertical. The bob of pendulum describes a horizontal circle and the string describes a cone.

Expression for Period of Conical Pendulum:

Let us consider a conical pendulum consists of a bob of mass ‘m’ revolving in a horizontal circle with constant speed ‘v’ at the end of a string of length ‘l’. Let the string makes a constant angle ‘θ’ with the vertical. let ‘h’ be the depth of the bob below the support.

The tension ‘F’ in the string can be resolved into two components. Horizontal ‘Fsin θ’ and vertical ‘Fcos θ’.

The vertical component (F cos θ) balances the weight mg of the vehicle.

F cosθ  = mg  ………….. (1)

The horizontal component (F sin θ) provides the necessary centripetal force.

F sin θ = mv²/r  ………… (2)

Dividing equation (2) by (1) we get,

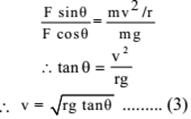
But v = rω
Where ω is angular speed and T is the period of the pendulum.

From figure tan θ = r/h

Substituting in equation (4)

This is an expression for the time period of a conical pendulum.

The time taken by the bob of a conical pendulum to complete one horizontal circle is called the time period of the conical pendulum

Notes:

The semi-vertical angle θ or angle made by the string with vertical depends on the length and period of the conical pendulum. If the time period decreases, then the quantity cosθ decreases. in turn θ increases. θ can never be 90° because for this period T = 0.

Expression for Tension in the String of Conical Pendulum:

Let us consider a conical pendulum consists of a bob of mass ‘m’ revolving in a horizontal circle with constant speed ‘v’ at the end of a string of length ‘l’. Let the string makes a constant angle ‘θ’ with the vertical. let ‘h’ be the depth of the bob below the support.

The tension ‘F’ in the string can be resolved into two components. Horizontal ‘Fsin θ’ and vertical ‘Fcos θ’.

The vertical component (F cos θ) balances the weight mg of the vehicle.

F cosθ = mg ………….. (1)

The horizontal component (F sin θ) provides the necessary centripetal force.

F sin θ = mv²/r ………… (2)

Dividing equation (2) by (1) we get,

Squaring equations (1) and (2) and adding

Substituting equation (5)

This is an expression for the tension in the string of a conical pendulum.

Notes:

A simple pendulum is a special case of a conical pendulum in which angle made by the string with vertical is zero i.e. θ = 0°.

Then the period of the simple pendulum is given by

For conical pendulum θ < 10° time period obtained is almost the same as the time period for simple pendulum having the same length as that of the conical pendulum. Hence when performing an experiment on a simple pendulum, the teacher advises not to increase θ beyond 10°.

Characteristics of Semi-vertical Angle of Conical Pendulum:

• The semi-vertical angle is the angle made by the string of conical pendulum with the vertical.
• It is given by the expression

• It is independent of the mass of the bob of the conical pendulum.
• The semi-vertical angle θ depends on the length and period of the conical pendulum. If the time period decreases, then θ increases.
• θ can never be 90° because for this period T = 0.

Factors Affecting Time Period of Conical Pendulum:

• The time period of a conical pendulum is given by

• The time period of a conical pendulum is directly proportional to the square root of its length.
• The time period of a conical pendulum is directly proportional to the square root of the cosine ratio of the semi-vertical angle that is the angle made by the string of conical pendulum with the vertical.
• The time period of a conical pendulum increases with the increase in the value of the semi-vertical angle.
• The time period of a conical pendulum is inversely proportional to the square root of the acceleration due to gravity at that place.
• The time period of a conical pendulum is independent of the mass of the bob of the conical pendulum.

Numerical Problems:

Example – 01:

A cord 5.0 m long is fixed at one end and to its other end is attached a weight which describes a horizontal circle of radius 1.2 m. Compute the speed of the weight in the circular path. Find its time period.

Given: Length of conical pendulum = l = 5.0 m, radius of circular path of bob = r = 1.2 m, g = 9.8 m/s²,

To find: velocity of weight = v =? Period = T = ?

Solution:

By Pythagoras theorem

Ans: The speed of the weight is 1.7 m/s, the period of the motion of the weight is 4.41 s.

Example – 02:

A stone of mass 1 kg is whirled in a horizontal circle attached at the end of 1 m long string making an angle of 30° with the vertical. Find the period and centripetal force if g = 9.8m/s².

Given: Length of pendulum = l = 1 m, angle with vertical = θ = 30°, g = 9.8 m/s²,

To find: Period = T =? Centripetal force = F = ?

Solution:

Ans: Period of motion = 1.867 s, Centripetal force = 5.657 N

Example – 03:

A string of length 0.5 m carries a bob of mass 0.1 kg with a period of 1.41 s. Calculate the angle of the inclination of the string with vertical and tension in the string.

Given:  Length of pendulum = l = 0.5 m, mass of bob = m = 0.1 kg, Period = T = 1.41 s, g = 9.8 m/s²,

To find:  The angle with vertical = θ =? Tension = F = ?

Solution:

For equilibrium, Total upward force = Total downward force

Ans: Angle of the string with vertical = 8°52’, The tension in string = 0.992 N

Example – 04:

A conical pendulum has a length of 50 cm. Its bob of mass 100 g performs a uniform circular motion in a horizontal plane in a circle of radius 30 cm. Find a) the angle made by the string with the vertical b) the tension in the string c) the period d) the speed of the bob e) centripetal acceleration of the bob f) centripetal and centrifugal force acting on the bob.

Solution:

Given: length of pendulum = l = 50 cm = 0.5 m, mass of bob = m = 100 g = 0.1 kg, radius of circle = r = 30 cm = 0.3 m, g = 9.8 m/s²,

To find:  Angle made with vertical = θ =? Tension = T =  ?, Period, Centripetal force = F = ?, centrifugal force = F = ?

Calculation of tension in string (In diagram F = T)

For equilibrium, Total upward force = Total downward force

Calculation of time period

Calculation of centrifugal force:

Ans: The angle of the string with vertical = 36°52’, The tension in the string = 1.225 N, Period = 1.27 s, The velocity of a bob = 1.48 m/s, Centripetal force = 0.73 N radially inward, Centrifugal force = 0.73 N radially outward

Note: The above explanations and problems are based on the assumption that the reference frame is inertial.

Period of a simple pendulum in Non-Inertial Reference Frame:

Reference frames which are at rest or moving with constant velocity with respect to the earth are called inertial reference frames.

Reference frames which are moving with acceleration with respect to the earth are called non-inertial reference frames. In the case of the non-inertial reference frame, we have to consider the pseudo force acting on the bob of the pendulum and corresponding changes should be done in the formula.

• For a simple pendulum oscillating in a vehicle moving horizontally with acceleration (a) the time period  is

The pendulum will make an angle θ = tan^-1(g/a)  with the vertical

• For a simple pendulum oscillating in a lift moving upward with acceleration (a) the time period of oscillation is

• For a simple pendulum oscillating in a lift moving downward with acceleration (a) the time period of oscillation is

• For a conical pendulum oscillating in a vehicle moving horizontally with acceleration (a) the time period is

The pendulum will make an angle θ + tan-1(g/a)  with the vertical

• For a conical pendulum oscillating in a lift moving upward with acceleration (a) the time period of oscillation is

• For  a conical pendulum oscillating in a lift moving downward with acceleration (a) the time period of oscillation is

Previous Topic: Numerical Problems on Banking of Road

Next Topic: Motion of Body in Vertical Circle

Science > Physics > Circular Motion > Conical Pendulum