Coulomb’s Law

Science > Physics > Electrostatics > Coulomb’s Law

In this article, we shall study the COulomb’s law of electrostatics, its explanation, uses, and limitations.

Coulomb’s Law of Electrostatics:

Statement:

The force of attraction or repulsion between two electric point charges is directly proportional to the product of the magnitude of the charges and inversely proportional to the square of the distance between the two charges. The force acts along the line joining the two charges.

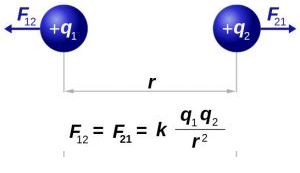
Explanation:

Let q₁ and q₂ be the two-point charges separated by distance ‘r’ in a medium with dielectric constant ‘k’  Then,

F  ∝ q₁ . q₂   ………..  (1)

F  ∝ 1/r²…………(2)

From statement (1) & (2) we get

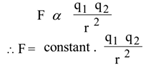
Where F   = force between the two charges,

∈_o  = electrical permittivity of free space. = 8.8542 × 10^-12 C² N^-1m^-2 or F m^-1.

k  = dielectric constant of the medium.

This expression is called a mathematical statement of Coulomb’s Law.

The value of the constant

Hence the equation of Coulomb’s law can be written as

In cgs system the value of 1/4πε_o = 1

Coulomb’s force is not affected by the presence or absence of other charges.

Coulomb’s Law in a Vector Form:

Where  F ₂₁ = Force on the second charge due to the first charge.

r ₁₂ = Unit vector from the first charge due to the second charge

Where  F ₁₂ = Force on the second charge due to the first charge.

r ₂₁ = Unit vector from the first charge due to the second charge

as unit vector r ₁₂ = – unit vector r ₂₁

 F ₂₁ = – F ₁₂

Thus the forces are equal but oppositely directed.

If we consider the signs of the charges (positive and negative) then the vector form of coulomb’s law can be written as

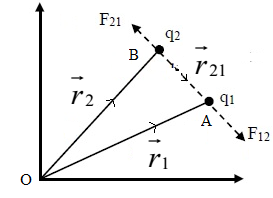
Coulomb’s Law in Terms of Position Vector:

Let r₁ and r₂  be the position vectors of charges q₁ and q₂ situated at point A and B respectively w.r.t. origin O.

By triangle law of vector addition

By Coulomb’s law, the force on charge q₁ due to charge q₂ is given by

This is the vector form of Coulomb’s law in terms of position vectors of charges.

Limitations of Coulomb’s law:

• Coulomb’s law is applicable to point charges only and is not applicable to extended bodies.
• It can be applied to extended bodies by assuming them to be point charges but the distance between them should be sufficiently large,
• The law holds good only for stationary charges.
• Coulomb’s law is verified for distances from 10^-15 m to several kilometres. We are not sure about its validity for a distance less than 10^-15 m (nuclear dimensions).

Notes:

• The charges possessing the same nature of charge are called like charges. Like charges either all positive or all negative. Like charges always repel each other.
• The charges possessing opposite nature of charge are called, unlike charges. Unlike charges always repel each other.

Dimensions of Electrical Permittivity:

Hence dimensions of universal electrical permittivity are [L^-3M^-1T⁴I²]

Units of charge:

Coulomb: SI unit of charge is coulomb.

Definition of Coulomb (Using Coulomb’s Law):

By Coulomb’s Law

If q₁ = q₂ = q, r = 1 m and F = 9 × 10⁹ N, k =1, then

q² = 1 and q = ± 1 C

The charge of 1 coulomb is that charge which, when placed in free space at a distance of 1 metre from an equal and similar charge, repels it with a force of  9 × 10⁹ N

Definition of Coulomb (Using Electric Current):

The electric current flowing through any section of a conductor is given by

I = q/t

Where q   =   electric charge flowing through any section of the conductor

t    =   time for which the charge is flowing

q = I × t

unit of charge = unit of a current × unit of time

1 coulomb = 1 ampere × 1 second

Hence a charge of 1 coulomb is defined as the quantity of a charge which flows per second through any cross-section of a conductor when there is a steady current of 1 ampere in the conductor.

statcoulomb or electrostatic unit (esu) of charge:

statcoulomb or esu of charge is cgs unit of charge. In cgs system the value of 1/4πε_o = 1

If q₁ = q₂ = q, r = 1 cm and F = 1 dyne, then

q² = 1 and q = ± 1 C

Hence one statcoulomb of a charge is that charge which, when placed in free space at a distance of 1 cm from an equal and similar charge, repels it with a force of 1 dyne. In cgs system unit of electromagnetic charge is abcoulomb or emu of charge.

Conversions:

From	To	Factor
coulomb (C)	statcoulomb or esu	x 3 x 109
emu	esu	x 3 x 1010
coulomb (C)	abcoulomb	x  0.1

Note:

These definitions are for convenience and not standard. When defining S.I. Unit coulomb in standard conditions help of the magnetic effect of electric current is considered.

Dielectric Constant of Medium:

Definition:

The ratio of the electrical permittivity of the medium to the electrical permittivity of free space is called the dielectric constant of the medium.

k = ∈ / ∈_o 

The dielectric constant of e medium is denoted by letter ‘k’ or ‘∈_r‘. As it is a pure ratio it has no unit. For air or vacuum k = 1 for any other medium k > 1.

Let q₁ and q₂ be the two point charges separated by distance ‘r’ in a medium in a vacuum, and then the same charges separated by the same distance in a medium with dielectric constant ‘∈_r‘.

Thus the dielectric constant or relative permittivity of a medium can be defined as the ratio of the electrostatic force between two charges separated by a certain distance in vacuum to the electrostatic force between the same two charges separated by the same distance in the medium. The presence of dielectric reduces electrostatic force between two charges which implies that the electrostatic force between two charges is maximum in a vacuum.

Comparison Between Electrostatic Force and Gravitational Force:

Points of Similarity:

• Both the forces obey the inverse square law of distances.
• Work done by both the forces does not depend on the path followed. Hence both the forces are conservative forces.
• Both the forces act along the line joining the centres of interacting bodies. Hence both the forces are central forces.
• Both the forces operate even in the vacuum.

Point of Dissimilarity:

• Gravitational force is always that of attraction while the electrostatic force may be attractive or repulsive depending upon the nature of interacting charges.
• Gravitational force is unaffected by the intervening medium. The electrostatic force depends on the dielectric constant of the intervening medium.
• The electrostatic force is very much stronger than the gravitational force. Let us consider an electron-proton system in an atom. The electrostatic force F_e and gravitational force F_g between them are given by

• We can see that the electrostatic force is 1039 times stronger than the gravitational force. But gravitational force plays a more significant role than the electrostatic force because most of the bodies in the universe are electrically neutral. Similarly, due to the attractive or repulsive nature of electrostatic force, they can cancel each other while gravitational force is only of attraction hence there is no question of cancellation of the gravitational force. Thus gravitational force is weak but has the dominating effect.
• Electrostatic forces are weaker than nuclear forces.

The principle of Superposition of Forces:

• This principle is used for calculation of net force acting on an individual charge due to other when more than two charges are interacting with each other.
• When a number of charges are interacting, the total force on a given charge is the vector sum of individual forces exerted on a given charge by all other charges.
• Let us consider a  system of point charges q1, q2, q3, q4, ……..qn.  Let F12, F13, F14, F15, ……..F1n be the forces acting on charge q1 due to charges q₂, q₃, q₄, ……..q_n respectively.
•  Then according to the principle of superposition of forces, the force acting on charge q₁ is given by

 F₁ =  F₁₂ + F₁₃ + F₁₄ +  ……+ F_1n

By vector representation

Applying the same logic to all such pairs we have

• The same procedure can be adopted for finding the force on any other charge due to the remaining charges.

Numerical Problems:

Example – 01:

The distance between electron and proton in a hydrogen atom is 5.3 × 10^-11 m. What is the magnitude of the electric force between them?

Given: Distance between proton and electron = r =  5.3 × 10^-11 m, The magnitude of the charge on proton = q₁ = 1.6 × 10^-19 C, Magnitude of the charge on electron = q₂ = 1.6 × 10^-19 C.

To find: Force =?

Solution:

By Coulomb’s law

Ans: The electric force between electron and proton is 8.202 × 10^-8 N.

Example – 02:

Two charges of magnitudes 1 μC and 2 μC are separated by a medium of dielectric constant 2. What is the magnitude of the electric force between them?

Given: Distance between proton and electron = r =  10 cm = 0.1 m, The magnitude of the first charge = q₁ = 1 μC = 1 × 10^-6 C, Magnitude of the charge on second charge = q₂ = 2 μC = 2 × 10^-6 C, dielectric constant of medium = k = 2.

To find: Force =?

Solution:

By Coulomb’s law

Ans: The electric force between the charges is 0.9 N.

Example – 03:

Two small spheres are charged positively. The combined charge being 5.0 x 10-5 C. If each sphere is repelled from other by a force of 1.0 N when they are 2.0 m apart. How is the total charge distributed between two spheres?

Given: Distance between two charges = r =  2.0 m, Sum of the cahrges = 5.0 × 10^-5 C =  50 × 10^-6 C, Let , The magnitude of the first charge = q₁ = q μC = q × 10^-6 C, Magnitude of the other charge = q₂ =(50 – q)  × 10^-6 C, dielectric constant of medium = k = 1. Force = F = 1.0 N

To find: charges = ?

Solution:

By Coulomb’s law

∴ q₁= 38.43 m C = 38.43 × 10^-6 C = 3.84 × 10^-5 C

∴ q₂= 11.57 m C = 11.57 × 10^-6 C = 1.16 × 10^-5 C

Ans: The distribution of charge is 3.84 × 10^-5 C and 1.16 × 10^-5 C

Science > Physics > Electrostatics > Coulomb’s Law