Critical Velocity and Time Period of Satellite

Science > Physics > Gravitation > Critical Velocity and Time Period of Satellite

In this article, we shall derive expressions for the critical velocity and time period of a satellite in different forms.

Critical Velocity:

The constant horizontal velocity given to the satellite so as to put it into a stable circular orbit around the earth is called critical velocity and is denoted by Vc. It is also known as orbital speed or proper speed.

The Expression for Critical Velocity:

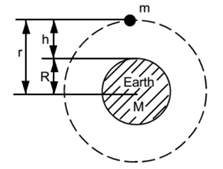
Let us consider a satellite of mass “m” orbiting at height “h” from the surface of earth around the earth with critical velocity V_c as shown in the diagram. Let M and R be the mass and radius of earth respectively. The radius ’r’ of the orbit is    r = R + h

The necessary centripetal force for the circular motion of satellite is provided by the gravitational attraction between the satellite and the earth.

Now, Centripetal force = Gravitational force

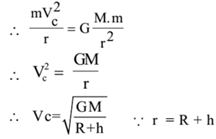
This is the expression for the critical velocity of a satellite orbiting around the earth at height h from the surface of the earth. The expression does not contain the term ‘m’. Hence we can conclude that the critical velocity of a satellite is independent of the mass of the satellite.

Expression for the Critical Velocity of Satellite Orbiting Very Close to Earth’s Surface:

If a satellite is orbiting very close to the earth’s surface i.e. h < < R then h may be neglected in comparison of R and Critical velocity may be given as

Expression for the Critical Velocity of Satellite in Terms of Acceleration Due to Gravity:

We have

Where g_h = acceleration due to gravity at height h from the surface of the earth.

This is an expression for the critical velocity of a satellite orbiting at height h in terms of acceleration due to gravity at that height.

If the satellite is orbiting very close to the earth’s surface then h < < R  and thus h can be neglected. Similarly near the surface of the earth g_h =  g i.e. the acceleration due to gravity on the surface of the earth.

This is an expression for the critical velocity of a satellite orbiting very close to the Earth’s surface.

Expression for the Critical Velocity of Satellite Orbiting Very Close to the Earth’s Surface in Terms of Density of the Material of the Earth / Planet:

The critical velocity of a satellite orbiting very close to the earth’s surface is given by

This is the expression for the critical velocity of a satellite orbiting very close to the earth’s surface in terms of density of the material of the earth/planet.

Factors Affecting Critical Velocity of Satellite:

• The critical velocity of the satellite is directly proportional to the square root of mass (M) of the planet (earth) around which the satellite is orbiting.
• It is inversely proportional to the square root of the radius of its orbit.
• The equation does not contain the term, ‘m’ which shows that the critical velocity is independent of the mass of the satellite.

Possibilities of Orbits of Satellites:

Depending upon Magnitude of Horizontal Velocity following four cases can arise for Motion of Satellite

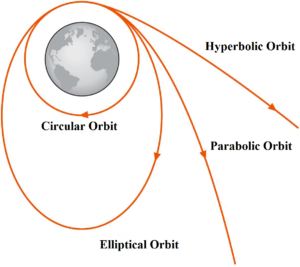
Case – 1 (v_h < v_c): If the horizontal velocity imparted to the satellite is less than critical velocity Vc, then the satellite moves in a long elliptical orbit with the centre of the Earth as the further focus. If the point of projection is apogee and in the orbit, the satellite comes closer to the earth with its perigee point lying at 180o. If enters the earth’s atmosphere while coming towards perigee, it will lose energy and spiral down on the earth. Thus it will not complete the orbit. If it does not enter the atmosphere, it will continue to move in an elliptical orbit.

Case – 2 (v_h = v_c): If the horizontal velocity imparted to the satellite is exactly equal to the critical velocity Vc then satellite moves in a stable circular orbit with the earth as centre as shown in the diagram.

Case – 3 (V_e > V_h > V_c): If the horizontal velocity Vh is greater than critical velocity Vc but less than escape velocity Ve then satellite orbits in
the elliptical path around the earth with the centre of the earth as one of the foci (nearer focus) of the elliptical orbit as shown.

Case – 4 (V_h > V_e): If the horizontal velocity is greater than or equal to escape velocity Ve then satellite overcomes the gravitational
attraction and escapes into infinite space along a hyperbolic trajectory.

Period of a Satellite:

The time taken by the satellite to complete one revolution around the planet is known as the period of revolution of the satellite. It is denoted by ‘T’.  Its S.I. unit is second.

Expression for Period of a Satellite:

Let us consider a satellite of mass “m” orbiting at height “h” from the surface of earth around the earth with critical velocity V_c as shown in the diagram. Let M and R be the mass and radius of earth respectively. The radius ’r’ of the orbit is    r = R + h

The necessary centripetal force for the circular motion of satellite is provided by the gravitational attraction between the satellite and the earth.

Now, Centripetal force = Gravitational force

Now the period of satellite ‘T’ is given by

This is the expression for the time period of a satellite orbiting around the earth at height h from the surface of the earth.

Squaring both sides of the above equation, we get

For the given planet the quantity in the bracket is constant hence we can conclude that

T²  ∝  r³

Thus the square of the period of a satellite is directly proportional to the cube of the radius of Its orbit. (Kepler’s third law of planetary motion)

Expression for the Periodic Time in Terms of Acceleration Due to Gravity:

Let g_h be the acceleration due to gravity at a point on the orbit i.e. at a height h above the earth’s surface.

This is an expression for the period of a satellite orbiting at height h in terms of acceleration due to gravity at that height.

If satellite orbiting very close to the earth (i.e. h < < R) then h can be neglected. Then r = R and    g_h = g

This is an expression for the time period of a satellite orbiting very close to the earth’s surface.

Expression for the Periodic Time of Satellite Orbiting Very Close to the Earth’s Surface in Terms of Density of the Material of the Earth / Planet:

The time period of a satellite orbiting around the earth is given by

If satellite orbiting very close to the earth  (i.e. h < < R) then h can be neglected. Then R + h = R

This is the expression for the period of a satellite orbiting very close to the earth’s surface in terms of density of the material of the earth/planet.

Factors Affecting Period of Satellite:

• The square of the time period of the satellite is directly proportional to the cube of the radius of orbit (r) of the satellite
• The equation does not contain the term, ‘m’ which shows that the critical velocity is independent of the mass of the satellite.

Previous Topic: Artificial Satellites and Their Uses

Next Topic: Numerical Problems on Critical Velocity and Period

Science > Physics > Gravitation > Critical Velocity and Time Period of Satellite