Science > Physics > Kinetic Theory of Gases > Degree of Freedom of Gas Molecules
In this article, we shall study the concept of degree of freedom of gas molecules. Degree of freedom for different types of gases. We shall also find the ratio of specific heats for different types of gases.
Degree of Freedom of a Gas Molecule:
A molecule free to move in space needs three coordinates to specify its location. If a molecule is constrained to move along a line it requires one co-ordinate to locate it. Thus it has one degree of freedom for motion in a line. If a molecule is constrained to move in a plane it requires two coordinates to locate it. Thus it has two degrees of freedom for motion in a plane. If a molecule is free to move in a space it requires three coordinates to locate it. Thus it has three degrees of freedom for motion in a space.
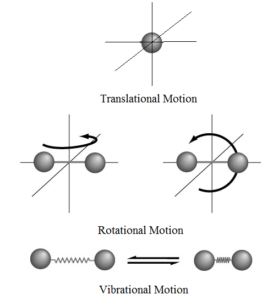
Law of Equipartition of Energy:
Statement: In equilibrium, the total energy is equally distributed in all possible energy modes, with each mode having average energy equal to

Explanation: A molecule has three types of kinetic energy a) Translational kinetic energy, b) Rotational kinetic energy, and c) Vibrational kinetic energy. Thus total energy of a molecule is given by
ET = ETranslational + ERotational + EVibrational ……… (1)
For translational motion, the molecule has three degrees of freedom (along the x-axis, along the y-axis and along the z-axis). Hence,
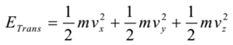
For rotational motion, it has two degrees of freedom along its centre of mass (clockwise and anticlockwise).

For vibrational motion only one degree of freedom (to and fro).

Where k is the force constant and y is the vibrational coordinate.
Thus the total energy of the molecule is

It is to be noted that in the vibrational mode the energy has two components potential and kinetic and by the law of equipartition energy, each part is equal to

Thus the total vibrational component of the energy is

Specific Heats of Gases:
In the case of solids and liquids, small change in temperature causes a negligible change in the volume and pressure, hence the external work performed is negligible. In such cases, all the heat supplied to the solid or liquid is used for raising the temperature. Thus there is only one value of specific heat for solids and liquids.
When gases are heated small change in temperature causes a considerable change in both the volume and the pressure. Due to which the specific heat of gas can have any value between 0 and ∞. Therefore to fix the values of specific heat of a gas, either the volume or pressure is kept constant. Hence it is necessary to define two specific heats of gases. viz. Specific heat at constant pressure and specific heat at constant volume.
Molar Specific Heat of Gas at Constant Volume:
The quantity of heat required to raise the temperature of one mole of gas through 1K (or 1 °C) when the volume is kept constant is called molar specific heat at constant volume. It is denoted by CV. Its S.I. unit is J K-1 mol-1.
Molar Specific Heat of Gas at Constant Pressure:
The quantity of heat required to raise the temperature of one mole of gas through 1K (or 1 °C) when pressure is kept constant is called molar specific heat at constant pressure. It is denoted by CP. Its S.I. unit is J K-1 mol-1.
Relation Between CP and CV :
CP – CV = R
This relation is known as the Mayor’s relation between the two molar specific heats of a gas.
The ratio CP/CV is known as ratio of specific heats and is denoted by the letter ‘γ’
Ratio of Specific Heats for Different Gases:
Monoatomic Gases:
Helium and argon are monoatomic gases. The monoatomic gases have only translational motion, hence they have three translational degrees of freedom. The average energy of the molecule at temperature T is given by

By the law of equipartition of energy we have

Thus the energy per mole of the gas is given by

Thus the ratio of specific heat capacities of monoatomic gas is 1.67
Diatomic Gases:
Dinitrogen, dioxygen, and dihydrogen are diatomic gases. The diatomic gases have translational motion (three translational degrees of freedom) as well as rotational motion(rotational degree of freedom). The average energy of the molecule at temperature T is given by

By the law of equipartition of energy we have

Thus the energy per mole of the gas is given by

Thus the ratio of specific heat capacities of diatomic gas is 1.4
Triatomic Gas:
Trioxygen (ozone) and carbondioxide are triatomic gases. The triatomic gases have translational motion, rotational motion as well as vibrational motion, hence has three translational degrees of freedom and two rotational degrees of freedom. For non-rigid molecules, there is an additional vibrational motion.
The average energy of the molecule at temperature T is given by

By the law of equipartition of energy we have

Thus the energy per mole of the gas is given by

Polyatomic Gases:
A polyatomic molecule has 3 translational, 3 rotational and certain number (say f) of vibrational modes. By the law of equipartition of energy, one mole of such gas has

Thus the energy per
mole of the gas is given by

This is an expression for the ratio of specific heats of polyatomic gases. Where f is the degree of freedom of vibration.
Polyatomic Gas having ‘f’ degree of Freedom:
By the law of equipartition of energy for ‘f’ degree of freedom we have

Thus the energy per mole of the gas is given by


The ratio of specific heats 1+ 2/f
The Expression for the Molar Specific Heat Capacity of Solid:
Consider a solid of N atoms, each vibrating about mean position. These atoms don’t have translational or rotational modes. The average energy of oscillation in one dimension is KBT. Thus the average energy of oscillation is 3KBT.
For one mole of Solid N = Avogadro’s number = NA.
Thus total energy

Since there is negligible change in the volume of a solid on heating, solids have only one specific heat.
∴ C = 3R
Molar Specific Heat Capacity of Water:
A water molecule has three atoms (2hydrogens and 1 oxygen). If we treat water like solid, the total energy of water molecules is three times the average energy of an atom of solid. Thus for Water

Previous Topic: Specific Heats of Gases
For More Topics in Physics Click Here