Elastic and Inelastic Collision

Science > Physics > Force >Elastic and Inelastic Collision

When two bodies moving along a straight line collide with each other the collision is called the head-on collision. In a head-on collision, the initial and the final velocities are along the same straight line.

Elastic Collision:

The collision in which the total kinetic energy, as well as total momentum, is conserved is called an elastic collision.

In a perfectly elastic collision, the relative velocity of the approach before the collision is equal to the relative velocity of separation after the collision.

Proof:

Let us consider two bodies having masses m₁ and m₂ moving in the same direction, along the same straight line with velocities u₁ and u₂ respectively ( u1  >  u2). Let v₁ and v₂ be their velocities after the collision. Since all the velocities are in the same direction, we can write the equation of conservation of momentum in scalar form.

m₁u₁+ m₂u₂ = m₁v₁+ m₂v₂

∴  m₁u₁ – m₁v₁   = m₂v₂–  m₂u₂

∴  m₁(u₁ – v₁)  = m₂₍v₂–  u₂)  ……….. (1)

For elastic collision, total kinetic energy before the collision is equal to total kinetic energy after collision.

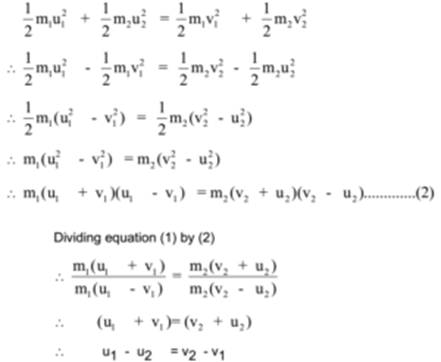
The quantity u₁ – u₂ is called the relative velocity of approach and the quantity v2 – v1 is called the velocity of separation. Thus for elastic collision, The relative velocity of the approach before the collision is equal to the relative velocity of separation after the collision.

Calculation of Final Velocities of Bodies:

Values of v1 and v2 can be found using values of u1 and u2 as follows.

We have,

u1  –  u2     = v2  – v1

v2   =   u1  –  u2   +  v1

Putting this value in equation (1) we have

    m1(u1 – v1)   =  m2( u1 + v1 – u2 – u2)

m1 u1 – m1v1   =  m2( u1 + v1 –  2 u2 )

m1 u1 – m1v1   = m2 u1 + m2 v1 –  2 m2 u2

m1 u1 – m2 u1 +  2 m2 u2  =   m1v1  + m2 v1

 m1v1  + m2 v1  =   m1 u1 – m2 u1 +  2 m2 u2

v1 ( m1  + m2 )  =   (  m1 – m2  ) u1 +  2 m2 u2

We have,

u1  –  u2     = v2  – v1

v1   =   u1  –  u2   – v2 

Putting this value in equation (1)

m1( u1 – v2 – u2 + u1)  =  m2(v2 – u2)

m1 ( 2 u1 – v2 – u2)  =  m2(v2 – u2)

2 m1u1 – m1v2 – m1u2  = m2 v2 – m2 u2

2 m1u1 – m1u2  +  m2 u2 = m2 v2 + m1v2

m2 v2 + m1v2   =  2 m1u1 – m1u2  +  m2 u2

( m2 + m1) v2   =  2 m1u1 + ( m2  –  m1 )u2

We should study following special cases.

Case – I

When two spheres have equal masses i.e. m₁ = m₂ =  m

Similarly

Thus, in this case, the two bodies exchange their velocities during a collision.

Case – II

The sphere B is at rest i.e. u₂ = 0

Similarly,

Further if m1  = m2  = m,

∴ v₁  =  0    and v₂  = u₁

Thus the body of mass m₁ is stopped cold and the body of mass m2 takes off with velocity which is equal to the initial velocity of the body of mass m1 before the collision.

Inelastic Collision:

The collision in which the total momentum is conserved but the total kinetic energy is not conserved is called the inelastic collision.

A collision between two bodies is said to be a perfectly inelastic collision if they stick to each other and moves together with common velocity after collision.

Let us consider two bodies having masses m₁ and m₂ moving in the same direction along the same straight line with velocities u₁ and u₂ respectively. ( u₁ >  u₂). Let v be the common velocity of the two bodies after the collision. Since all the velocities are in the same direction, we can write the equation of conservation of momentum in scalar form.

m₁u₁ +   m₂u₂ =   m₁v  +  m₂v

m₁u₁  +   m₂u₂ =   ( m₁ +  m₂)v

Since the quantities on the right sides are positive. The initial kinetic energy is always greater than the final kinetic energy in a perfectly inelastic collision.

When two bodies collide with each other part of its kinetic energy gets converted into sound energy, heat energy, etc. Therefore, total kinetic energy after collision decreases due to the loss of K.E.

The Coefficient of Restitution:

The ratio of the relative velocity of separation to the relative velocity of approach, in a collision between two bodies, is called the coefficient of restitution. It is denoted by e.

For perfectly elastic collision e = 1 , For perfectly inelastic collision e = 0, for all other collisions 0  <  e   <  1

Action and reaction are two forces equal in magnitude and opposite in direction. Why they do not cancel each other?

When two forces having the same magnitude and opposite direction act on the same body their effect is canceled. Action and reaction forces are equal in magnitude and opposite in direction but they act on two different bodies. Therefore they do not cancel each other.

Previous Topic: The law of Conservation of Momentum

Next Topic: Moment of Force

Science > Physics > Force >Elastic and Inelastic Collision