Moment of Inertia of Standard Bodies

Science > Physics > Rotational Motion Moment of Inertia of Standard Bodies

In this article, we shall study the method of deriving an expression for moment of inertia of a body.

Expression for Moment of Inertia of Uniform Rod About a Transverse Axis Passing Through its Centre:

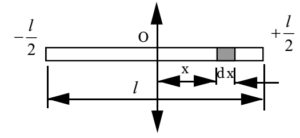
Consider a thin uniform rod, of mass M, an area of cross-section A, length l, and density of material ρ. Let us consider an infinitesimal element of length dx at a distance of x from the given axis of rotation.  Then its Moment of Inertia about the given axis is given by

dI = x² . dm,  …… (1)

But,   Mass =  Volume x Density

∴   dm    =  A . dx . ρ  ……   (2)

From Equations (1) and (2)

dI  =    x² A . dx .ρ

∴ dI  = A .ρ . x² . dx

The moment of inertia I of the rod about. the given axis is given by

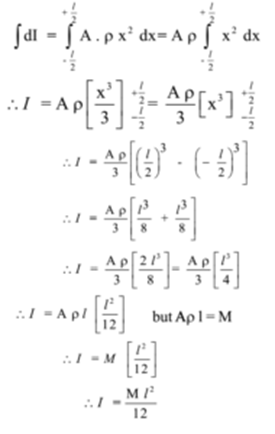
This is an expression for moment of inertia of a thin uniform rod about a transverse axis passing through its centre.

Expression for Moment of Inertia of a Uniform Rod About a Transverse Axis Passing Through its End:

Method – I:

Consider a thin uniform rod, of mass M, an area of cross-section A, length l, and density of material ρ. Let us consider an infinitesimal element of length dx at a distance of x from the given axis of rotation.  Then its Moment of Inertia about the given axis is given by

dI = x² . dm,  …… (1)

But,   Mass =  Volume x Density

∴   dm    =  A . dx . ρ  ……   (2)

From Equations (1) and (2)

dI  =    x² A . dx .ρ

∴ dI  = A .ρ . x² . dx

The moment of inertia I of the rod about. the given axis is given by

This is an expression for moment of inertia of a thin uniform rod about a transverse axis passing through its end.

Expression for the Moment of Inertia of an Annular Ring:

Consider a uniform thin annular disc of mass M having inner radius R₁, outer radius R₂, thickness t, and density of its material ρ. Let us assume that disc is capable of rotating about a transverse axis passing through its centre. Let us assume that the disc is made up of infinitesimally thin rings.

Consider  one such ring of radius r and width dr.  Moment of Inertia of such element is  given, by,

dI  =   r² . dm   ………….. (1)

But,      Mass   =    volume × density

dm  =  ( 2 π r . dr .  t) ρ   ………  (2)

From Equation (1) and (2)

dI  =   r² . ( 2 π r . dr .  t) ρ

dI  =   2 π t  ρ  r³ . dr .

The moment of inertia I of the annular disc will be given by

Where M is the total mass of the annular ring.

This is an expression for moment of inertia of annular ring about a transverse axis passing through its centre.

Expression for Moment of Inertia of a Thin Uniform Disc About a Transverse Axis Passing Through its Centre and Perpendicular to its Plane:

The moment of inertia of annular ring about a transverse axis passing through its centre is given by

For the solid disc, there is no centre hole, hence R₂ =   R and R₁ = 0

This is an expression for moment of inertia of thin uniform disc about a transverse axis passing through its centre.

Expression for Moment of Inertia of a Thin Uniform Ring About an Axis Passing through its Centre and Perpendicular to its Plane:

The moment of inertia of annular ring about a transverse axis passing through its centre is given by

For ring, the centre hole extends up to its periphery, hence R₂ =   R and R₁ =R

This is an expression for moment of inertia of thin uniform ring about a transverse axis passing through its centre.

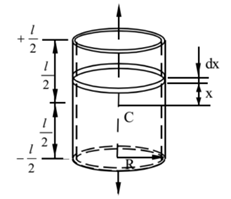
Expression for Moment of Inertia  of a Solid Cylinder About its Geometrical Axis:

Consider a solid cylinder of mass M, length ‘’ and radius ‘r’ capable of rotating about its geometrical axis. Let ‘m be its mass per unit length.

m = M/l      Hence M = m . l

A solid cylinder can be regarded as a number of thin uniform discs of infinitesimal thickness piled on top of one another. Let us consider one such disc of thickness ‘dx’ at a distance of ‘x’ from the centre C of the cylinder.

Mass of such disc is given by

Mass, dm = m.dx   =  (M /l). dx

The M.I. of such disc about a transverse axis (passing through C) is given by

Integrating the above expression in limits

This is an expression for M. I. of a solid cylinder about its geometrical axis.

Expression for Moment of Inertia of a Hollow Cylinder About its Geometrical Axis:

Consider a hollow cylinder of mass M, length ‘’ and radius ‘r’ capable of rotating about its geometrical axis. Let ‘m be its mass per unit length.

m = M/l      Hence M = m . l

A hollow cylinder can be regarded as a number of thin uniform rings of infinitesimal thickness piled on top of one another. Let us consider one such ring of thickness ‘dx’ at a distance of ‘x’ from the centre C of the cylinder.

Mass of such ring is given by

Mass, dm = m.dx  = (M/ l) dx

The M.I. of such ring about a transverse axis (passing through C) is given by

This is an expression for M. I. of a solid cylinder about its geometrical axis.

Expression for Moment of Inertia of a Solid Sphere About its Diameter (Geometrical axis):

Let us consider a solid homogeneous sphere of radius ‘R’ and mass ‘M’, capable of rotating about its diameter. Let us consider a circular strip of infinitesimal thickness ‘dx’ at a distance of x from centre ‘O’. The radius of this circular strip is PM, which is given by

This circular strip can be treated as thin disc rotating about a transverse axis passing through its centre.

The M.I. of the disc about a transverse axis passing through its centre is given by

The M.I. of the whole sphere about diameter can be obtained by integrating the above expression.

The mass of the sphere = M. Hence, the M.I. of the solid homogeneous sphere is given by

This is an expression for M.I. of a solid sphere about its diameter (Geometrical axis).

Previous Topic: Principles of Parallel and Perpendicular Axes

Next Topic: Applications of Parallel and Perpendicular Axes

Science > Physics > Rotational Motion Moment of Inertia of Standard Bodies