Science > Physics > Stationary Waves > Numerical Problems Vibration of String Set-02
In this article, we shall study to solve problems to calculate fundamental frequency of vibration of string and its higher frequencies.
Example 01:
A stretched wire emits a fundamental note of 256 Hz. Keeping the stretching force constant and reducing the length of wire by 10 cm, the frequency becomes 320 Hz. Calculate the original length of wire.
Given: Initial frequency = n1 = 256 Hz, Final frequency = n2 = 320 Hz, Initial length = l1 = l, Final length = l2 = (l – 10) cm
To Find: Original length of wire = l =?
Solution:
By law of length
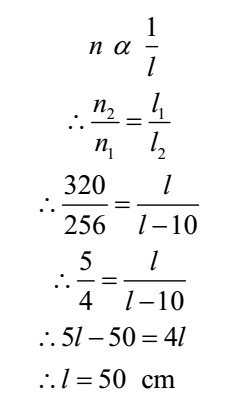
Ans: Original length of wire = 50 cm
Example 02:
The vibrating length of a sonometer wire under tension is 1.11 m. Where should two bridges be placed to divide the wire into three segments whose fundamental frequencies are in the ratio 4:5:6?
Given: Total length of wire = 1.11 m, Ratio of frequencies n1: n2: n3 = 4:5:6
To Find: Lengths of segments =?
Solution:
Let the lengths of segments be l1, l2, and l3.
By law of length
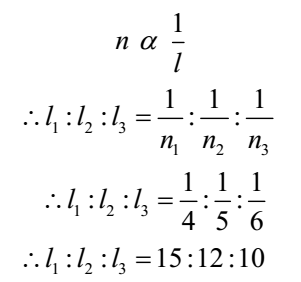
Now l = l1 + l2 + l3
∴ 1.1 = 15k + 12k + 10k
∴ 37k = 1.11
∴ k = 0.03
∴ l1 = 15k = 15 x 0.03 = 0.45 m
∴ l2 = 12k = 12 x 0.03 = 0.36 m
∴ l3 = 10k = 10 x 0.03 = 0.30 m
Ans: The bridges should be placed at 045 m and 0.45 + 0.36 = 0.81 m from end.
Example 03:
The vibrating length of a sonometer wire under tension is 105 cm. Where should two bridges be placed to divide the wire into three segments whose fundamental frequencies are in the ratio 1:3:15?
Given: Total length of wire = 105 cm, Ratio of frequencies n1: n2: n3 = 1:3:15
To Find: Lengths of segments =?
Solution:
Let the lengths of segments be l1, l2, and l3.
By law of length
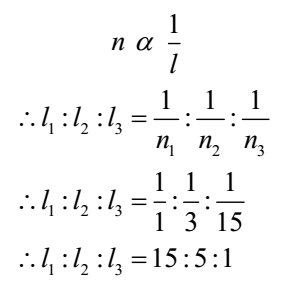
Now l = l1 + l2 + l3
∴ 105 = 15k + 5k + k
∴ 21k = 105
∴ k = 5
∴ l1 = 15k = 15 x 5 = 75 cm
∴ l2 = 5k = 5 x 5 = 25 cm
∴ l3 = 1k = 1 x 5 = 5 cm
Ans: The bridges should be placed at 75cm and 75 + 25 = 100 cm from end.
Example 04:
Find the fundamental frequency of vibration of a wire 40 cm long under tension T if the velocity of waves along the wire is 160 m/s. What should be the tension if the wire is to emit a note of frequency an octave higher when vibrating in the same mode?
Given: Length of wire = l = 40 cm = 0.4 m, Tension in wire = T, Velocity of wave = 160 m s-1,
To Find: Fundamental frequency = n =? Tension =? When frequency n2 = 2n (octave)
Solution:
For fundamental mode of vibration wavelength of wave λ = 2l = 2 × 0.4 = 0.8 m
We have v = nλ
∴ n = v/λ = 160/0.8 = 200 Hz
By law of tension, we have

Ans: Fundamental frequency = 200 Hz and Tension required for obtaining octave = 4T
Example 05:
On increasing the tension in a given string by 2.5 kg, the frequency of vibration is increased in the ratio 3:2. Find the original stretching weight.
Given: Initial tension = T1 = T, Final tension = T2 = T + 2.5 kg, n2 : n1 = 3:2,
To Find: Initial tension = T =?
Solution:
By law of tension

∴ 9T = 4T + 10
∴ 5T = 10
∴ T = 2 kg wt = 2 x 9.8 = 19.6 N
Ans: Original stretching force is 2 kg wt i.e. 19.6 N
Example 06:
On increasing the tension in a given string by 5 kg, the frequency of vibration is increased in the ratio 2:3. Find the original stretching weight.
Given: Initial tension = T1 = T, Final tension = T2 = T + 5 kg, n2 : n1 = 3:2,
To Find: Initial tension = T =?
Solution:
By law of tension

∴ 9T = 4T + 20
∴ 5T = 20
∴ T = 4 kg wt = 4 x 9.8 = 39.2 N
Ans: Original stretching force is 4 kg wt i.e. 39.2 N
Example 07:
A stretched wire under a tension of 4 kg-wt is in unison with a tuning fork of frequency 512 Hz. How should be tension be altered to make the wire vibrate in unison with a tuning fork of frequency 256 Hz?
Given: Initial tension = T1 = 4 kg wt, Initial frequency = n1 = 512 Hz, Final frequency = n2 = 256 Hz.
To Find: Change in tension =?
Solution:
By law of tension

∴ T2 = 1 kg wt
∴ Change in tension = 4 – 1 = 3 kg wt = 3 x 9.8 = 29. 4 N
Ans: The tension should be decreased by 29.4 N
Example 08:
A string of a sonometer emits a sound of frequency 150 Hz. If the tension is changed in the ratio 9: 16 and the length of the wire is doubled, calculate the frequency of the fundamental note emitted by the string.
Given: Initial length of wire = l1 = l, Final length of wire = l2 = 2l, Ratio of tension in wire = T1/T2 = 9/16, Initial frequency = n1 = 150 Hz
To Find: Final frequency = n2 =?
Solution:
Fundamental frequency of vibration of string is given by

Ans: The new fundamental frequency = 100 Hz
Example 09:
A stretched string has a fundamental frequency of 100 Hz. What would the fundamental frequency be if the length and the tension are both increased by 5%?
Given: Initial length of wire = l1, Final length of wire = l2 = l1 + 5% l1 = 1.05 l1 , Initial tension = T1, Final length of wire = T2 = T1 + 5%T1 = 1.05 T1, Initial fundamental frequency = n1 = 100 Hz
To Find: Final frequency = n2 =?
Solution:
Frequency of fundamental mode of vibration of string is given by

Ans: The new fundamental frequency = 97.6 Hz
Example 10:
A stretched wire has a frequency of 300 Hz. If its length is doubled and the tension is trebled, what will be the frequency?
Given: Initial length of wire = l1, Final length of wire = l2 = 2l1, Initial tension = T1, Final length of wire = T2 = 3T1, Initial fundamental frequency = n1 = 300 Hz
To Find: Final frequency = n2 =?
Solution:
Frequency of fundamental mode of vibration of string is given by

Ans: The new frequency = 259.8 Hz
Example 11:
A sonometer wire under tension T is replaced by another wire of the same length and material but with double the diameter. How should the tension be adjusted to keep the frequency of vibration the same?
Solution:
Given: length of wire = l1 = l2 , Density of material of wire = ρ1 = ρ2, diameter of wire = d2 = 2d1, Frequency same = n1 = n2.
To Find: New tension=?
Solution:
Frequency of fundamental mode of vibration of string is given by

Ans: Tension should made 4 times the original value.
Example 12:
Compare the frequencies for the same mode of vibration of two strings under tensions of 156 N and 39 N respectively. They are each one metre in length and are of same diameter but their densities are 8 x 103 kg m-3and 2 x 103 kgm-3 respectively.
Given: length of wire = l1 = l2 = 1m, diameter of wire = d1 = d2, Tensions T1 = 156 N, T2 = 39 N, Density of material of wire = ρ1 = 8 x 103 kg m-3 and ρ2 = 2 x 103 kgm-3,
To Find: n1/n2 =?
Solution:
Frequency of fundamental mode of vibration of string is given by

Ans: Two frequencies are equal.
Example 13:
Two wires of the same material and of the same diameter have their lengths in the ratio 1 : 3 and are under tensions in the ratio 1:4.Compare their fundamental frequencies.
Given: length of wire l1 : l2 = 1 : 3, diameter of wire = d1 = d2, Material same ρ1 = ρ2, Tensions T1 : T2 = 1 : 4.
To Find: n1/n2 =?
Solution:
Frequency of fundamental mode of vibration of string is given by

Ans: Ratios of fundamental frequencies is 3:2.
Example 14:
A string B has twice the length, twice the diameter, twice the tension and twice the density of another string A. Which overtone of B will have the same frequency of the fundamental as A?
Given: length of wire lB = 2lA, diameter of wire dB = 2dA, Material same ρB = 2ρA, Tensions TB = 2TA.
To Find: n1/n2 =?
Solution:
Frequency of fundamental mode of vibration of string is given by

Ans: Frequency of string B is third overtone of that of string A
Example 15:
Two vibrating wires under tension when vibrating in the fundamental mode have lengths in the ratio 3 : 4, tensions in the ratio 5 : 6 and linear densities in the ratio 4 : 5. If the frequency of vibration of one wire is 256 Hz, find that of the other.
Given: length of wire l1 : l2 = 3 : 4, Linear density m1 : m2 = 4 : 5, Tensions T1 : T2 = 5 : 6.
To Find: n2 =?
Solution:
Frequency of fundamental mode of vibration of string is given by

Ans: Frequency of other wire is 188.1 Hz
Example 16:
Two wires vibrating in the fundamental mode have diameters in the ratio 3 : 5, lengths in the ratio 4 : 3 and are under tensions in the ratio 3 : 2. The densities of material of the wires are in the ratio 1.5 : 1. If the smaller frequency of vibration is 256 Hz, find that of the other.
Given: Diameters d1: d2 = 3: 5, length of wire l1: l2 = 4:3, Tensions T1 : T2 = 3 : 2, Densities of material of wire ρ1 : ρ2 = 1.5:1, Smaller frequency = 256 Hz.
To Find: Higher frequency =?
Solution:
Frequency of fundamental mode of vibration of string is given by

Thus, n1 < n2, hence n2 = 256 Hz
Ans: Fundamental frequency of other wire is 320 Hz.