Graphical Representation of S.H.M.

Science > Physics > Oscillations: Simple Harmonic Motion > Graphical Representation of S.H.M.

In this article, we shall study graphical representation of S.H.M. i.e. variation in displacement, velocity, and acceleration with time for a body performing S.H.M. starting from a) the mean position and b) from the extreme position.

Graphical Representation of Linear S.H.M. of a Particle Starting from Mean Position:

The general equation for the displacement of a particle performing linear S.H.M. at any instant ‘t’ is given by

x = a  sin (ωt + α )

Where a = amplitude of S.H.M., ω = angular speed of S.H.M.,

α = Initial phase of S.H.M.

As particle is starting from mean position, α = 0

x  =  a  sin ωt   …….. (1)

Velocity of particle performing S.H.M.can be obtained by differentiating above expression

v = dx/dt = a cos ωt . ω = ωa cos ωt

v =  ωa cos ωt   …….. (2)

Acceleration of particle performing S.H.M. can be obtained by differentiating above expression

f = dv/dt = ωa (-sin ωt)  ω

f = dv/dt = – ω²a sin ωt    …….. (3)

From equation (1) and (3) we have

f = dv/dt = – ω²x    …….. (4)

Using equations (1), (2) and (4) and knowing ω = 2π/T we prepare following table

Time (t)	Phase Φ = ωt = (2π/T)t	Displacement (x)	Velocity (v)	Acceleration (f)
0	0	0	aω	0
T/4	π/2	a	0	– aω²
T/2	π	0	– aω	0
3T/4	3π/2	– a	0	a ω²
T	2π	0	aω	0

The graphs of displacement, velocity and acceleration versus time are as follows:

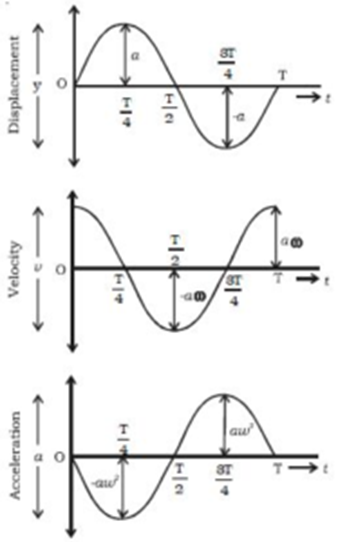
Graphical Representation of Linear S.H.M. of a Particle Starting from Extreme Position:

The general equation for displacement of a particle performing linear S.H.M. at any instant ‘t’ is given by

x = a  sin (ωt + α )

Where a = amplitude of S.H.M., ω = angular speed of S.H.M., α = Initial phase of S.H.M.

As particle is starting from mean position, α = π/2

x = a  sin (ωt + π/2 )

x  =  a  cos ωt   …….. (1)

Velocity of particle performing S.H.M.can be obtained by differentiating above expression

v = dx/dt = a (- sin ωt) . ω = – ωa sin ωt

v =  – ωa sin ωt …….. (2)

Acceleration of particle performing S.H.M. can be obtained by differentiating above expression

f = dv/dt = – ωa (cos ωt)  ω

f = dv/dt = – ω²a cos ωt    …….. (3)

From equation (1) and (3) we have

f = dv/dt = – ω²x    …….. (4)

Using equations (1), (2) and (4) and knowing ω = 2π/T we prepare following table

Time (t)	Phase Φ = ωt = (2π/T)t	Displacement (x)	Velocity (v)	Acceleration (f)
0	0	a	0	– aω²
T/4	π/2	0	aω	0
T/2	π	– a	0	aω²
3T/4	3π/2	0	– aω	0
T	2π	a	o	– aω²

The graphs of displacement, velocity and acceleration versus time are as follows:

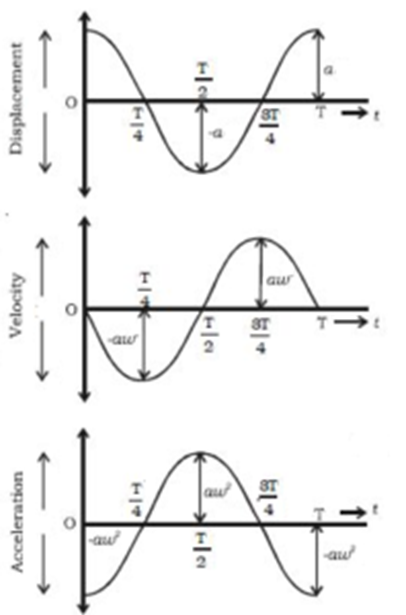
Conclusions:

• Graphs are drawn for displacement, velocity and acceleration against time and curves are obtained as shown.  As the curves have the shape same as the sine curve, the curves are called as harmonic curves.
• From the graph, we can conclude that the displacement, velocity, and acceleration are the periodic functions of time.
• From the graph, we can see that velocity is 90° (π/2 radians) out of phase with displacement, whereas acceleration is 180° (π radians) out of phase with displacement. Similarly, acceleration is 90° (π/2 radians) out of phase with velocity.
• The velocity leads the displacement by a phase difference of π/2 radians.
• The acceleration lags behind displacement by a phase of π radians.
• The displacement and acceleration are maximum at the extreme position while velocity is minimum at the same position. Similarly, the displacement and acceleration are minimum at the mean position while velocity is maximum at the same position.
• All curves repeat after a phase of 2π radians.

Previous Particle: Numerical Problems on Velocity and Acceleration of a Body Performing S.H.M.

Next Topic: Energy of Particle Performing S.H.M.

Science > Physics > Oscillations: Simple Harmonic Motion > Graphical Representation of S.H.M.