Numerical Problems on Newton’s Law of Gravitation

Science > Physics > Gravitation > Numerical Problems on Newton’s Law of Gravitation

In this article, we shall learn numerical problems to calculate the gravitational force of attraction between two bodies.

Example – 01:

Calculate the gravitational force of attraction between two metal spheres each of mass 90 kg, if the distance between their centres is 40 cm. Given G = 6.67 x 10^-11 N m²/kg². Will the force of attraction be different if the same bodies are taken on the moon, their separation remaining the same?

Given: Mass of first body = m₁ = 90 kg, mass of second body = m₂ = 90 kg, Distance between masses = r = 40 cm = 40 x 10^-2 m, G = 6.67 x 10^-11 N m²/kg² .

To Find: Force of attraction = F =?

Solution:

By Newton’s law of gravitation

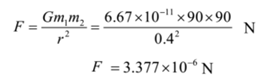
If the same bodies are taken on the moon, their separation remaining the same, the force of attraction between the two bodies will remain the same, because the force of attraction between two bodies is unaffected by the presence of the third body and medium between the two bodies.

Ans: The force of attraction between two metal spheres is 3.377 x 10^-6 N

The force of attraction between two bodies remains the same

Example – 02:

Find the gravitational force of attraction between the moon and the earth if the mass of the moon is 1/81 times the mass of earth. G = 6.67 x 10^-11 N m²/kg², radius of moon’s orbit is 3.58 x 10⁵ km. Mass of the earth = 6 x 10²⁴ Kg.

Given: Mass of Moon =  1/81 times the mass of earth, m_m = 1/81 m_e ,Distance between the moon and earth  = r = 3.58 x 10⁵ km = 3.58 x 10⁸ m, G = 6.67 x 10^-11 N m²/kg² . Mass of earth = M_e = 6 x 10²⁴ Kg

To Find: Force of attraction = F =?

Solution:

By Newton’s law of gravitation

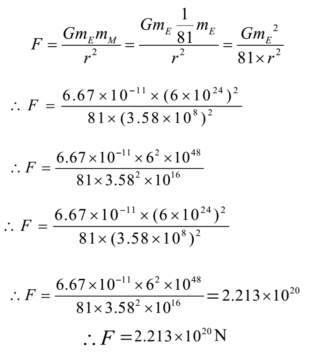
Ans: The gravitational force of attraction between the moon and the earth is 2.213 x 10²⁰ N

Example – 03:

Two bodies of masses 5 kg and 6 x 10²⁴ kg are placed with their centres 6.4 x 10⁶ m apart. Calculate the gravitational force of attraction between the two masses. Also, find the initial acceleration of two masses assuming no other forces act on them.

Given: Mass of first body = m₁ = 5 kg, mass of second body = m₂ = 6 x 10²⁴ kg, Distance between masses = r = 6.4 x 10⁶ m, G = 6.67 x 10^-11 N m²/kg² .

To Find: Force of attraction between two masses = F =? Initial accelerations of the two masses =?

Solution:

By Newton’s law of gravitation

Initial acceleration of body of mass 5 kg

By Newton’s second law of motion F = ma

Thus a = F/m = 48.85 / 5 = 9.77 m/s²

Initial acceleration of body of mass 6 x 10²⁴ kg

By Newton’s second law of motion F = ma

Thus a = F/m = 48.85 / 6 x 10²⁴ = 8.142 x 10^-24 m/s²

Ans: The force of attraction between the two masses = 48.85 N

The Initial acceleration of body of mass 5 kg is 9.77 m/s² and

That of body of mass 6 x 10²⁴ kg is 8.142 x 10^-24 m/s².

Example – 04:

A sphere of mass 40 kg is attracted by another spherical mass of 15 kg by a force of 9.8 x 10^-7 N when the distance between their centres is 0.2 m. Find G.

Given: Mass of first body = m₁ = 40 kg, mass of second body = m₂ = 15 kg, force between them = F = 9.8 x 10^-7 N, Distance between the masses = r = 0.2 m.

To Find: Universal gravitation constant = G =?

Solution:

By Newton’s law of gravitation

Ans: The value of universal gravitation constant is 6.533 x 10^-11 N m²/kg².

Example – 05:

A sphere of mass 100 kg is attracted by another spherical mass of 11.75 kg by a force of 19.6 x 10^-7 N when the distance between their centres is 0.2 m. Find G.

Given: Mass of first body = m₁ = 100 kg, mass of second body = m₂ = 11.75 kg, distance between masses = r = 0.2 m, force between them = F =  19.6 x 10^-7 N,

To Find: Universal gravitation constant = G =?

Solution:

By Newton’s law of gravitation

Ans: The value of universal gravitation constant is 6.672 x 10^-11 N m²/kg².

Example – 06:

The distance of a planet from the earth is 2.5 x 10⁷ km and the gravitational force between them is 3.82 x 10¹⁸ N. Mass of the planet and earth are equal, each being 5.98 x 10²⁴ kg. Calculate the universal gravitation constant.

Given: Mass of Planet = m₁ = 5.98 x 10²⁴ kg, mass of earth = m₂ = 5.98 x 10²⁴ kg, distance between them = r = 2.5 x 10⁷ km = 2.5 x 10¹⁰ m, force between them = F =  19.6 x 10^-7 N,

To Find: Universal gravitation constant = G =?

Solution:

By Newton’s law of gravitation

Ans: The value of universal gravitation constant is 6.676 x 10^-11 N m²/kg².

Example – 7:

Three 5 kg masses are kept at the vertices of an equilateral triangle each of side of 0.25 m. Find the resultant gravitational force on any one mass. G = 6.67 x 10^-11 S.I. units.

Given:  m₁ = 5 kg, m₂ = 5 kg, m₃ = 5 kg, r = 0.25 m, G = 6.67 x 10^-11 N m²/kg².

To find: Force on m₁ =?

Solution:

By Newton’s law of gravitation, the force on mass m₁ due to mass m₂.

By Newton’s law of gravitation, the force on mass m₁ due to mass m₃.

The angle between F₁₂ and F₁₃ is 60°. (Angle of an equilateral triangle). The net force on m₁ is given by

The two forces are equal, hence their resultant act along angle bisector towards centroid.

Ans:  Force on any mass is 4.621 x 10^-8 N towards the centroid

Previous Topic: Theory of Newton’s Law of Gravitation

Next Topic: Concept of Gravitational Intensity

Science > Physics > Gravitation > Numerical Problems on Newton’s Law of Gravitation