In this article, we shall study the concept of radioactive decay, decay constant, and half life of radioactive substance.
Transformation of radioactive element into another element (radioactive or non-radioactive) is known as radioactive decay or disintegration. In radioactive decay, the nucleus of a radioactive element called parent undergoes a spontaneous change accompanied by the emission of radiation and the formation of the nucleus of a new element called the daughter. The physical and chemical properties of the daughter may be different from its parent.
Rate of Radioactive Decay:
The total number of active atoms of a given radio elements disintegrating in unit time is called radioactive decay rate or rate of radioactive disintegration. The rate of radioactive disecay of a radioactivity substance is also called the activity of that radioactive substance.
Let ‘dN’ be the number of atoms disintegrating in short time interval of ‘dt’, then – dN/dt represent the rate of radioactive decay. The negative sign indicates that the rate of radioactive decay goes on decreasing with time. The rate of radioactive decay is independent of temperature, pressure, presence of catalyst, state of existence etc.
Units of Radioactivity:
The activity of a radioactive substance is measured by the rate of disintegration of that substance in unit time. The traditional unit of activity of radioactive substance is curie (c).
- The curie is defined such that 3.7 x 1010 disintegrations take place per second in a radioactive substance, then the activity of the substance is 1 curie.
Thus 1 c = 3.7 x 1010 disintegrations/second.
Smaller units are millicurie (mc) and microcurie (µc)
1 mc = 3.7 x 107 disintegrations/second.
1 µc = 3.7 x 104 disintegrations/second.
- Another unit to measure the activity of a radioactive substance is Rutherford (Rd)
1 Rd = 106 integrations per second
1 mRd = 103 disintegrations/second.
1 µRd = 1 disintegrations/second.
- S. I. unit of the activity of a radioactive substance is becquerel (Bq)
1 Bq = 1 disinegration per second
1 c = 3.7 x 1010 Bq
- Note:
1 c = 3.7 x 1010 disintegrations/second = 3.7 x 1010 Bq = 3.7 x 104 Rd
Rutherford and Soddy Law of Radioactive Decay:
At any instant, the rate of disintegration of any radioactive substance is directly proportional to the number of radioactive atoms present at that instant and is independent of the physical and chemical condition of the substance.
The statement of the law indicates that the total amount of radioactive element goes on decreasing with time, the amount which disintegrates in unit time also goes on decreasing. Thus radioactive decay is an exponential process and it follows an exponential law.
Let ‘dN’ be the number of atoms disintegrating in a short time interval of dt, then, dN/dt represents the rate of radioactive decay. By the law of radioactive decay or disintegration law
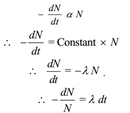
Where λ is called decay constant. It is definite or constant for given radio elements.
Definition of the Decay Constant:
The fraction of the total number of active atoms of a given radioactive element disintegrating in unit time is called decay constant. Its unit is per min or per day or per year depending upon the unit of half-life period.
Expression for Decay Constant of a Radioelement:
By law of radioactive decay “At any instant the rate of disintegration of any radioactive substance is directly proportional to number of radioactive atoms present at that instant and is independent of physical and chemical
condition of the substance.
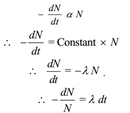
Where λ is called decay constant.
Let No be the initial amount of radioactive substance when t 1 = 0. Let N be the final amount of the radioactive substance at t2 = t. On integrating above expression between respective limits,
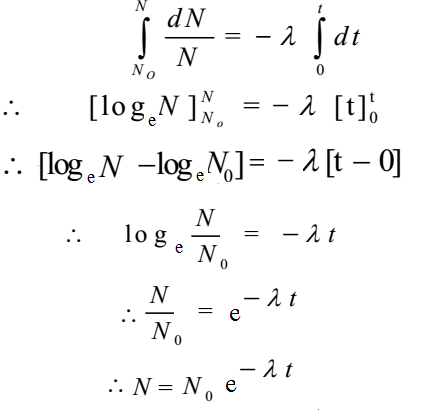
This relation shows that the radioactive decay is an exponential process. Initially the rate of decay is high and it decreases continuously.
Alternate Expression for the Law:
We have proved
Alternate Definition of Decay Constant:

Thus in a radioactive material, after a time-interval equal to the reciprocal of the decay constant the undecayed atoms are 36.8%. Using this property the radioactive decay constant can be defined as the reciprocal of the time during which the number of atoms in a radioactive substance reduces to 36.8% of their initial number.
The decay constant can also be defined as the reciprocal of time when the ratio N/No falls to 1/e.
Half-life Period of Radioelement:
The time taken by a radioactive element to disintegrate half of its initial amount is called as half-life period of that substance.
It is denoted by ‘T‘. The half-life period of a given radio element is definite. Its value changes from element to element or we can say that it is a characteristic property of the radioactive element.
Expression for Half-life Period of Radioelement:
By law of radioactive decay we have

Above equation indicates that, the half-life period is inversely proportional to the decay constant. It also shows that the product of half-life period of radioactive element and decay constant of the radioactive element is constant.
Characteristics of Half-life Period:
- The half-life period of a given radio element is definite. Its value changes from element to element or we can say that it is a characteristic property of the radioactive element. Hence it is useful in differentiating radioactive elements from one another.
- Half-life period is independent of external factors like temperature, pressure, presence of a catalyst, and state of existence of the element.
- It is independent of the original amount of the radioactive element.
- It is inversely proportional to decay constant.
Radioactive Decay is Exponential Process:
The process can be explained on the definition of half-life period. The time taken by a radioactive element to disintegrate half of its initial amount is called as half-life period. Let us assume a radioactive substance having half-life period of T. Let initial amount of the radioactive substance be No. Then quantity of radioactive substance remaining at the end of specific years is as follows. A curve is obtained by plotting the values of amount of radioactive element versus time.

As the time elapses the quantity goes on decreasing and hence the curve moves downward. But it never touches the X- axis (time axis). Hence we can say that the radioactive material will take infinite time to disintegrate completely. Hence the process is exponential process
Number of Atoms Left after n Half-lives:
Number of atoms remained after 1 half-life
N = No/2 = No (1/2) = No (1/2)1
Number of atoms remained after 2 half-lives
N = No/4 = No (1/4) = No (1/2)2
Number of atoms remained after 3 half-lives
N = No/8 = No (1/8) = No (1/2)3
Thus the number of atoms remained after n half-lives
N = No (1/2)n
Mean or Average Life of Radioactive Substance:
The average of all the lives of all the atoms in radioactive substance is called mean life or average life of that radioactive substance. It is denoted by τ.
It can be shown that the mean life of a radioactive substance is equal to the reciprocal of decay constant.
τ = 1/λ = 1/(0.9931/T) = T/0.6931 = 1.443 T
Thus average life is longer than half-life. The reason is that the last few atoms of the radioactive substance have very long lives.