Science > Physics > Oscillations: Simple Harmonic Motion > Numerical Problems on Maximum Velocity and Maximum Acceleration.
Example – 1:
a particle executing simple harmonic motion has a period of 6 s and its maximum velocity during oscillations is 6.28 cm/s. Find the time taken by it to describe a distance of 3 cm from its equilibrium position.
Given: Period = T = 6 s, Vmax = 6.28 cm/s, x = 3 cm, particle passes through mean position, α = 0.
To Find: Time taken = t =?
Solution:
Angular velocity = ω = 2π/T = 2π/6 = π/3 rad/s
vmax = ωa
∴ a = vmax/ω = 6.28 /(π/3) = 6 cm
Displacement of a particle performing S.H.M. is given by
x = a sin (ωt + α)
∴ 3 = 6 sin ((π/3)t + 0)
∴ 3/6 = sin ((π/3)t)
∴ (π/3)t = sin-1(1/2) = π/6
∴ t = 1/2 s = 0.5 s
Ans: Time taken = 0.5 s
Example – 2:
The maximum velocity of a particle performing simple harmonic motion is 6.28 cm/s. If the length of its path is 8 cm, calculate its period.
Given: path length = 8 cm, amplitude = 8/2 = 4 cm, Vmax = 6.28 cm/s,
To Find: Period = T =?
Solution:
vmax = ωa
∴ ω = vmax/a = 6.28/4 = 1.57 rad/s
T = 2π /ω = (2 x 3.14)/ 1.57 = 4 s
Ans: Period = 4 s
Example – 3
A particle performs simple harmonic motion of amplitude 3 cm. If its acceleration in the extreme position is 27 cm/s2, find the period.
Given: Amplitude = a = 3 cm, acceleration at extreme position = f = 27 cm/s2,
To Find: Period = T =?
Solution:
At extreme position acceleration is maximum, fmax = 27 cm/s2
fmax = ω2a
∴ ω2 = fmax/a = 27/3 = 9
∴ ω = 3 rad/s
T = 2π /ω = (2 x 3.14)/ 3 = 2.09 s
Ans: Period = 2.09 s
Example – 4:
A particle executing S.H.M. has a maximum velocity of 0.16 cm/s and a maximum acceleration of 0.64 m/s2. Calculate its amplitude and the period of oscillations.
Given: vmax = 0.16 cm/s, f max = 0.64 m/s2.
To Find: Amplitude = a =? and Period = T = ?
Solution:
fmax = ω2a ………. (1)
vmax = ωa ………. (2)
Dividing equation (1) by (2)
fmax /vmax = ω
∴ ω = 0.64/0.16 = 4 rad/s
Substituting in equation (2)
0.16 = 4 x a
∴ a = 0.04 cm
T = 2π /ω = (2 x 3.14)/ 4 = 1.57 s
Ans: amplitude = 0.04 cm and period = 1.57 s
Example – 5:
A block is on a piston which is moving vertically up and down with simple harmonic motion of period one second. At what amplitude of motion will the block and piston separate? At which point in the path of motion will the separation take place?
Given: Period = T = 1s
To Find: amplitude = a = ?
Solution:
Angular velocity = ω = 2π/T = 2π/1 = 2π rad/s
At the topmost point, the block and piston will separate.
At topmost point acceleration is maximum. Hence force is maximum
Maximum force on the block = weight of the block
m. fmax = mg
∴ fmax = g
∴ ω2a = g
∴ a = g / ω2 = 980/ (2 x 3.142)2 = 24.82 cm
Ans: At amplitude = 24.82 cm block will separate at the topmost point of the path
Example – 6:
A particle performs simple harmonic motion with a period of 12 s. If its velocity is 6 cm/s two seconds after crossing the mean position, what is the amplitude of its motion?
Given: Period = T = 12 s, v = 6 cm/s, time elapsed = t = 2 s, particle passes through mean position, α = 0.
To Find: amplitude = a =?
Solution:
Angular velocity = ω = 2π/T = 2π/12 = π/6 rad/s
Displacement of a particle performing S.H.M. is given by
x = a sin (ωt + α)
∴ x = a sin ( π/6 x 2 + 0)
∴ x = a sin ( π/3) = a √3/2 cm
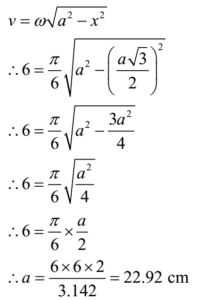
Ans: The amplitude of motion is 22.92 cm
Example – 7:
A particle in simple harmonic motion has a velocity of 10 cm/s when it crosses the mean position. If the amplitude of its oscillations is 2 cm, find the velocity. When it is midway between the mean and extreme positions.
Given: Velocity at mean position = vmax = 10 cm/s, amplitude = a = 2 cm, Displacement midway between the mean and extreme positions, hence x = a/2 = 2/2 = 1 cm.
To Find: Velocity = v =?
Solution:
We have vmax = ωa
∴ 10 = ω x 2
∴ ω = 10/2 = 5 rad/s
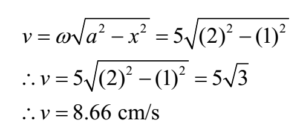
Ans: velocity at midway between the mean and extreme positions is 8.66 cm/s
Example – 8:
Show that the velocity of a particle performing simple harmonic motion is half the maximum velocity at a displacement of √3/2 times its amplitude.
Given: Displacement x = a√3/2
To Show: v = 1/2 vmax.
Solution:

Example – 9:
A particle performs S.H.M. of amplitude 10 cm. Its maximum velocity during oscillations is 100 cm/s. What is its displacement when the velocity is 60 cm/s?
Given: amplitude = 10 cm, Vmax = 100 cm/s, v = 60 cm/s
To Find: displacement = x =?
Solution:
vmax = ωa
∴ ω = vmax/a = 100/10 = 10 rad/s

Ans: Displacement = 8 cm
Example – 10:
A particle performing S.H.M. along a straight line has a velocity of 4π cm/s when its displacement is √12 cm. If the maximum acceleration it can attain is 16π2 cm/s2, find the amplitude and the period of its oscillations.
Given: vmax = 4π cm/s, f max = 16π2 m/s2 , Displacement = √12 cm
To Find: Amplitude = a =? and Period = T = ?
Solution:

fmax = ω2a
∴ 16π2 = ω2a ………. (2)
From equations (1) and (2) we have
ω2(a2 – 12) = ω2a
∴ (a2 – 12) = a
∴ a2 – 12 – a = 0
∴ (a – 4)(a + 3) = 0
∴ a = 4 cm or a = – 3 cm
Amplitude is maximum displacement hence a = 3 cm < √12 cm is not possible.
∴ a = 4 cm
substituting in equation (2)
16π2 = ω2(4)
∴ ω2 = 4π2
∴ ω = 2π rad/s
∴ T = 2π /ω = 2π /2π = 1 s
Ans: amplitude = 4 cm and period = 1 s
Example – 11
A particle of mass of 10 g performs S.H.M. of period 5 s and has an amplitude of 8 cm. Find its velocity when it is at a distance of 6 cm from the equilibrium position. Find also the maximum velocity and maximum force acting on it.
Given: mass = m = 10 g, Period = T = 5 s, amplitude = a = 8 cm, displacement = x = 6 cm, particle passes through mean position, α = 0.
To Find: velocity = v = ?, vmax = ?, Fmax = ?
Solution:
Angular velocity = ω = 2π/T = 2π/5 rad/s

∴ vmax = ωa = 2π/5 x 8 = 10.05 cm/s
fmax = ω2a = ( 2π/5)2 x 8 = 12.63 cm/s2
Fmax = m. fmax = 10 x 12.63 = 126.3 dyne
∴ Fmax = 126.3 x 10-5 N = 1.263 x 10-3 N
Ans: velocity =6 .65 cm/s; maximum velocity =10.05 cm/s; maximum force = 1.263 x 10-3 N
Example – 12:
If a particle performing S.H. M. starts from the extreme position after an elapse of what fraction of the period will the velocity of the particle be half the maximum velocity?
Given: v = 1/2 vmax. particle starts from extreme position, α = π/2.
Fo Find: Fraction of time = t/T =?
Solution:

∴ 4a2 – 4x2 = a2
∴ 4x2 = 3a2
∴ 2x = a√3
∴ x = a√3/2
Displacement of a particle performing S.H.M. is given by
x = a sin (ωt + α)
∴ a√3/2 = 1 sin ((2π/T)t + π/2)
∴ 3/2 = cos ((2π/T)t)
∴ (2π/T)t = cos-1(3/2) = π/6
∴ t /T = 1/12 s
Ans: fraction of the period is 1/12 s
Example – 13:
A particle performs a linear S.H.M. Its velocity is 3 cm/s when it is at 4 cm from the mean position and 4 cm/s when it is at 3 cm from the mean position. Find the amplitude and the period of S.H.M.
Given: v1 = 3 cm/s at x1 = 4cm and v2 = 4 cm/s at x2 = 3cm
To Find: Amplitude = a =? Period = T=?
Solution:

∴ 16a2 -256 = 9a2 -81
∴ 16a2 – 9a2 = 256 – 81
∴ 7a2 = 175
∴ a2 = 25
∴ a = 5

Now T = 2π/ω = 2 x 3.14 /1 = 6. 28 s
Ans: Amplitude = 5 cm and period = 6.28 s
Example – 14
The velocities of a particle performing linear S.H.M. are 0.13 m/s and 0.12 m/s when it is at 0.12 m and 0.13 m respectively from the mean position. Find its period and amplitude.
Given: v1 = 0.13 m/s = 13 cm/s at x1 = 0.12 m = 12 cm and v2 = 0.12 m/s = 12 cm/s at x2 = 0.13 m = 13 cm
To Find: Amplitude = a =? Period = T=?
Solution:

∴ 144a2 – 144 x 144 = 169a2 – 169x 169
∴ 169a2 – 144a2 = 169 x 169 – 144x 144
∴ 25a2 = (169 + 144)(169 – 144)
∴ 25a2 = (313)(25)
∴ a2 = 313
∴ a = √313 = 17.69 m

Now T = 2π/ω = 2 x 3.14 /1 = 6. 28 s
Ans: Period =6.28 s and amplitude = 17.69 cm
Example – 15:
A particle performing S.H.M. has velocities of 8 cm/s and 6 cm/s at displacements of 3 cm and 4 cm respectively. Find its amplitude and frequency of oscillations. Calculate its maximum velocity. What is the phase of its motion when the displacement is 2.5 cm?
Solution:
Given: v1 = 8 cm/s at x1 =3 cm and v2 = 6 cm/s at x2 = 4 cm, displacement = x = 2.5 cm
To Find: Amplitude = a =? frequency = n = ?, phase = (ωt + α) =?,

∴ 9a2 – 81 = 16a2 – 256
∴ 16a2 – 9a2 = 256 – 81
∴ 7a2 = 175
∴ a2 = 25
∴ a = 5 cm

Now ω = 2 π n
∴ n = ω/2π = 2/( 2 x 3.142) = 0.3183 Hz
Displacement of a particle performing S.H.M. is given by
x = a sin (ωt + α)
∴ 2.5 = 5 sin (ωt + α)
∴ sin (ωt + α) = 2.5/5 = 1/2
∴ (ωt + α) = sin-1(1/2) = π/6
Ans: Amplitude is 5 cm, frequency = 0.3183 Hz, Phase = π/6 or 30°
Next Topic: Graphical Representation of S.H.M.