Numerical Problems on Simple Harmonic Progressive Wave

Science > Physics > Wave Motion > Numerical Problems on Simple Harmonic Progressive Wave

Example – 01:

The equation of transverse simple harmonic progressive wave is y = 3 sin 2π(t/0.04 – x/40), where the length is expressed in cm and the time in seconds. Calculate the wavelength, frequency, amplitude and the speed of the wave.

Given: Equation of the wave y =3 sin 2π(t/0.04 – x/40) cm

To Find: Wavelength = λ =? Frequency = n =? Amplitude = a =? speed of wave = v =?

Solution:

Equation of given wave is

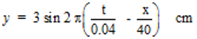
Comparing with

Amplitude = a = 3 cm, Period = T = 0.04 s, Wavelength = λ = 40 cm

We have n = 1/T = 1/0.04 = 25 Hz

Now, v = n λ = 25 × 40 = 1000 cm/s

Ans: Wavelength = 40 cm, Frequency = 25 Hz, Amplitude = 3 cm, speed of wave = 1000 cm/s = 10 m/s

Example – 02:

The equation of a certain sound wave (simple harmonic progressive wave) is given by y = 0.05 sin 10π(t/0.025 – x/8.5), where x and y are in meters and t is in seconds. What are the (1) amplitude (2) frequency (3) wavelength of the wave? What is the velocity and direction of propagation of the wave?

Given: Equation of the wave y = 0.05 sin 10π(t/0.025 – x/8.5) m

To Find: Amplitude = a =? Frequency = n =?,  Wavelength = λ = ?,  speed of wave = v =? and direction = ?

Solution:

Equation of given wave is

Comparing with

Amplitude = a = 0.05 m, Period = T = 0.005 s, Wavelength = λ = 1.7 m

We have n = 1/T = 1/0.005 = 200 Hz

Now, v = n λ = 200 × 1.7 = 340 m/s

The term – x/1.7 shows that the wave is moving in positive direction of x-axis

Ans: Amplitude =0.05 m, Frequency = 20 Hz,  Wavelength = 1.7 m,

Speed of wave = v = 340 m/s and direction = in positive direction of x-axis

Example-03:

The equation of a wave can be represented by y = 0.02 sin 2π /0.5 (320t – x) where x and y are in metres and t is in seconds. Find the amplitude, frequency, wavelength, and velocity of propagation of the wave.

Given: Equation of the wave y = y = 0.02 sin 2π /0.5 (320t – x) m

Solution:

To Find: Amplitude = a =? Frequency = n =? Wavelength = λ = ?  velocity of wave = v =?

Comparing with

Amplitude = a = 0.02 m, Frequency = n = 640 Hz, Wavelength = λ = 0.5 m

Now, v = n λ = 640 × 0.5 = 320 m/s

Ans: Amplitude =0.02 m, Frequency =640 Hz, Wavelength = 0.5 m, velocity of wave = 320 m/s

Example – 04:

A simple harmonic progressive wave of amplitude 5 cm and frequency 5 Hz is traveling along the positive X-direction with a speed of 40 cm/s. Calculate (1) the displacement at x = 38cm and t = 1 second. (2) the phase difference between two points in the path of the wave separated by a distance of 0.8 cm. (3) the phase difference between two positions of a particle at an interval of 0.01 s.

Given: Amplitude = a = 5 cm, Frequency = n = 5 Hz, Velocity = v = 40 cm/s, Direction = + X-axis.

To Find: 1) Displacement = y =? when x = 38cm and t = 1 second. 2) ∅ =? when x = 0.8 cm. 3) ∅ = ? when t = 0.01 s.

Solution:

We have v = n λ

∴ λ = v/n  =40/5 = 8m

The equation of progressive wave is in the form

1) Displacement = y =? when x = 38cm and t = 1 second.

2) ∅ = ? when x = 0.8 cm.

3) ∅ = ? when t = 0.01 s.

Example – 05:

The equation of progressive wave is y= 0.01 sin 2π (2t – 0.01x) when all quantities are expressed in SI units. Calculate (a) frequency of the wave. (b) the phase difference between two positions of the same particle at a time interval of 0.25 s. (c) phase difference at a given instant of time between two particles 50 m apart.

Given: Equation of wave y= 0.01 sin 2π (2t – 0.01x) m

To Find: 1) Frequency = n =?  2) ∅ =? when t = 0.25 s. 2) ∅ = ? when x = 50 m.

Solution:

Equation of wave y= 0.01 sin 2π (2t – 0.01x) m

Comparing with

Amplitude = a = 0.01 m, Frequency = n = 2 Hz, Wavelength = λ = 100 m

1) ∅ = ? when t = 0.25 s.

 2) ∅ = ? when x = 50 m.

Example – 06:

The equation of a simple harmonic progressive wave is given by y= 0.002 sin 2π(5t – x/12) where all the quantities are in S.I. units. Calculate the displacement of the particle at a distance of 5 m from the origin after 0.2 s.

Given: Equation of wave y= 0.002 sin 2π(5t – x/12) m

To Find: Displacement of particle = ?.

Solution:

Equation of wave y= 0.002 sin 2π(5t – x/12) m

∴   y = 0.002 sin 2π(5(0.2) – 5/12)

∴   y = 0.002 sin 2π(1 – 5/12)

∴   y = 0.002 sin 2π(7/12)

∴   y = 0.002 sin 7π/6

∴   y = 0.002 sin (6π + π)/6

∴   y = 0.002 sin (π + π/6)

∴   y = – 0.002 sin (π/6)

∴   y = – 0.002 × ½ = – 0.001 m

Ans: Displacement of partiocle = -0.001 m

Example – 07:

The equation of simple harmonic progressive wave of a source is y = 6 sin300πt cm. Write down the equation of the wave. Find the displacement, velocity and acceleration of a point 1.5 m from the source at the instant t = 0.01 s after the start of oscillations. The velocity of propagation of waves is 300 m/s.

Given: Equation of source is y = 6 sin300πt cm, v = 300 m/s

To Find: 1) displacement = y =?, Velocity of point = v = ?,  Acceleration of point = ?, at x = 1.5 m and t = 0.01 s.

Solution:

Equation of source is y = 6 sin300πt cm

Comparing with

y = a sin 2πn t cm and y = a sin ω t cm

Amplitude = a = 6 cm = 0.06 m, 2πn = 300 π, n = 150 Hz, ω = 300 π rad/s

We have v = n λ

∴ λ = v/n  = 300/150 = 2 m

Hence equation of the wave is

∴   y= 0.06 sin 2π(150t – x/2)

∴   y = 0.06 sin 2π(150(0.01) – 1.5/2)

∴ y = 0.06 sin 2π(1.5 – 0.75)

∴ y = 0.06 sin 2π(0.75)

∴ y = 0.06 sin 2π(3/4)

∴ y = 0.06 sin (3π/2)

∴  y = 0.06 (-1) = – 0.06 m

Velocity of particle is given by

Magnitude of the acceleration of particle is given by

f = ω²y = (300 π)² × 0.06 = 5.33 × 10⁴ m/s²

Example – 08:

The equation of simple harmonic oscillations of a source is y = 10 sin 20πt cm. Find the displacement from the position of equilibrium, the velocity and acceleration of point 10 m away from the source 3 seconds after oscillations begin. The velocity of propagation of waves 200 m/s.

Given: Equation of source is y = 10 sin 20πt cm, v = 200 m/s

To Find: 1) displacement = y =?, Velocity of point = v = ?,  Acceleration of point = ?, at x = 10 m and t = 3 s.

Solution:

Equation of source is y = 10 sin 20πt cm

Comparing with

y = a sin 2πn t cm and y = a sin ω t cm

Amplitude = a = 10 cm = 0.1 m, 2πn = 20 π, n = 10 Hz, ω = 20 π rad/s

We have v = n λ

∴ λ = v/n  = 200/10 = 20 m

Hence equation of the wave is

∴   y = 0.1 sin 2π(10t – x/20)

∴ y = 0.1  sin 2π(10(3) – 10/20)

∴ y = 0.1 sin 2π(30 – 1/2)

∴ y = 0.1 sin 2π(59/2)

∴ y = 0.1 sin 59π

∴ y = 0.1 (0) = 0 m

Magnitude of the velocity of particle is given by

Magnitude of the acceleration of particle is given by

f = ω²y = (20 π)² × 0 = 0  m/s²

Example – 09:

A transverse simple harmonic progressive wave of amplitude 0.01 m and frequency 500 Hz is traveling along a stretched string with a speed of 200 m/s. Find the displacement of the particle at a distance of 0.7 m from the origin and after 0.01 s.

Given: Amplitude = a = 0.01 m, frequency = n = 500 Hz, Velocity of wave = v = 200 m/s

To Find: 1) displacement = y =? at x = 0.7 m and t = 0.01 s.

Solution:

We have v = n λ

∴ λ = v/n  = 200/500 = 0.4 m

Hence equation of the wave is

∴   y = 0.01 sin 2π(500t – x/0.4)

∴   y = 0.01 sin 2π(500(0.01) – 0.7/0.4)

∴   y = 0.01 sin 2π(5 – 7/4)

∴   y = 0.01 sin 2π(13/4)

∴   y = 0.01 sin (13π/2)

∴   y = 0.01 sin (12π + π)/2

∴   y = 0.01 sin (6π + π/2)

∴   y = 0.01 sin (π/2)  = 0.01 × 1 = 0.01 m

Previous Topic: Theory of Simple Harmonic Progressive wave

Next Topic: Reflection of waves

Science > Physics > Wave Motion > Numerical Problems on Simple Harmonic Progressive Wave