Science > Physics > Current Electricity > Numerical Problems on Internal Resistance of Cell
Example 01:
A steady P.D. is maintained between the ends of the potentiometer wire. A cell of e.m.f. 1.02 V is on an open circuit when its terminals are in contact with two points on the wire distant 150 cm. When the cell is shunted by a resistance of 4 ohms, this distance reduces to 120 cm. Find the internal resistance of the cell.
Given: e.m.f of a cell = e = 1.02 V, Balancing length when circuit is open = l = 150 cm = 1.5 m, Balancing length when cell is shunted l1 = 120 cm = 1.2 m, Value of shunt = R = 4 ohm.
To Find: Internal resistance of cell = r =?
Solution:
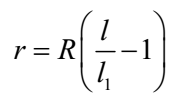
r = 4 x ((1.5/1.2) – 1) = 4 x (1.25 – 1)
r = 4 x 0.25 = 1 ohm
Ans: Internal resistance of the cell is 1 ohm
Example 02:
A steady P.D. is maintained between the ends of the potentiometer wire. A Daniel cell when in an open circuit is balanced by a length of 108 cm. When the cell is shunted by a resistance of 10 ohms, the balancing length reduces to 90 cm. Find the internal resistance of the cell.
Given: Balancing length when circuit is open = l = 108 cm = 1.08 m, Balancing length when cell is shunted l1 = 90 cm = 0.9 m, Value of shunt = R = 10 ohm.
To Find: Internal resistance of cell = r =?
Solution:
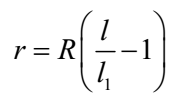
r = 10 x ((1.08/0.9) – 1) = 10 x (1.2 – 1)
r = 10 x 0.2 = 2 ohm
Ans: Internal resistance of the cell is 2 ohm
Example 03:
A steady P.D. is maintained between the ends of the potentiometer wire. A cell when in an open circuit is balanced by a length of 1.812 m. When the cell is shunted by resistance of 5 ohms, the balancing length reduces to 1.51 m. Find the internal resistance of the cell.
Given: Balancing length when circuit is open = l = 1.812 m, Balancing length when cell is shunted l1 = 1.51 m, Value of shunt = R = 5 ohm.
To Find: Internal resistance of cell = r =?
Solution:
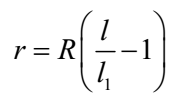
r = 5 x ((1.812/1.51) – 1) = 5 x (1.2 – 1)
r = 5 x 0.2 = 1 ohm
Ans: Internal resistance of the cell is 1 ohm
Example 04:
A potentiometer wire of length 4 m and resistance 8 ohms is connected in series with a battery of e.m.f. 2 V and negligible internal resistance. If the e.m.f. of cell balances against the length of 217 cm of the wire, find the e.m.f. of the cell. When a cell is shunted by a resistance of 15 ohms, the balancing length is reduced by 17 cm. Find the internal resistance of a cell.
Part 1:
Given: Length of potentiometer wire = lAB = 4m, Resistance of potentiometer wire = RAB = 8 ohm, Applied e.m.f = E = 2 V, Internal resistance = r = 0, Balancing length by cell = 217 cm = 2.17 m.
To Find: e.m.f. of cell = e =?
I = E/RAB = 2/8 = 0.25 A
VAB = I x RAB = 0.25 x 8 = 2 V
Potential Drop = VAB/lAB = 2/4 = 0.5 V m-1
E.m.f. of cell = Potential drop x Balancing length
E.m.f. of cell = 0.5 x 2.17 = 1.085 V
Part 2:
Given: Balancing length when circuit is open = l = 2.17 m, Balancing length when cell is shunted l1 = 2.17 m – 17 cm = 2.17 m – 0.17 m = 2 m, Value of shunt = R = 15 ohm.
To Find: Internal resistance of cell = r =?

r = 15 x ((2.17/2) – 1) = 15 x (1.085 – 1)
r = 15 x 0.085 = 1.275 ohm
Ans: E.m.f. of the cell is 1.085 V and internal resistance of the cell is 1.275 ohm
Example 05:
A cell balances against a length of 150 cm on potentiometer wire when it is shunted by resistance of 5 ohms. The balancing length reduces to 175 cm when it is shunted by a resistance of 10 ohms. Find the balancing length when the ell is in an open circuit.
To Find: Balancing length of the cell when in open circuit = l =?
Solution:
Let ‘l’ be the balancing length when the cell is in open circuit
Case 1: Balancing length when cell is shunted l1 = 150 cm = 1.5 m, Value of shunt = R = 5 ohm.
Case 2: Balancing length when cell is shunted l1 = 175 cm = 1.75 m, Value of shunt = R = 10 ohm.

From equations (1) and (2)

Ans: Balancing length of the cell when in open circuit is open is 2.1 m
Example 06:
A cell balances against a length of 250 cm on potentiometer wire when it is shunted by a resistance of 10 ohms. The balancing length reduces to 200 cm when it is shunted by resistance of 5 ohms. Find internal resistance of the cell.
To Find: Internal resistance of cell = r =?
Solution:
Let ‘l’ be the balancing length when cell is in open circuit
Case 1: Balancing length when cell is shunted l1 = 250 cm = 2.5 m, Value of shunt = R = 10 ohm.
Case 2: Balancing length when cell is shunted l1 = 200 cm = 2 m, Value of shunt = R = 5 ohm.

From equations (1) and (2)

Substituting in equation (1)

Ans: Internal resistance of the cell is 10/3 ohm
Example 07:
A cell balances against a length of 250 cm on potentiometer wire when it is shunted by resistance of 5 ohms. The balancing length reduces to 400 cm when it is shunted by a resistance of 20 ohm. Find internal resistance of the cell.
To Find: Internal resistance of cell = r =?
Solution:
Let ‘l’ be the balancing length when the cell is in open circuit
Case 1: Balancing length when cell is shunted l1 = 250 cm = 2.5 m, Value of shunt = R = 5 ohm.
Case 2: Balancing length when cell is shunted l1 = 400 cm = 4 m, Value of shunt = R = 20 ohm.

From equations (1) and (2)

Substituting in equation (1)

Ans: Internal resistance of the cell is 5 ohm
Previous Topic: Numerical Problems on Potential Drop