Introduction to Refraction of Light

Science > Physics > Refraction of Light > Introduction to Refraction of Light

Refraction of Light:

When light ray travelling in one optically active medium enters another optically active medium, then the light ray deviates from its path. This phenomenon is known as the refraction of light.

Laws  of Refraction:

• The ratio of the sine of the angle of incidence to the sine of the angle of refraction is always constant and is equal to the refractive index of the medium.  This law is known as Snell’s law.
• The incident ray and the refracted ray lie on the opposite side of the normal at the point of incidence.
• The incident ray, refracted ray and the normal at the point of incidence lie in the same plane.

Terminology of Refraction:

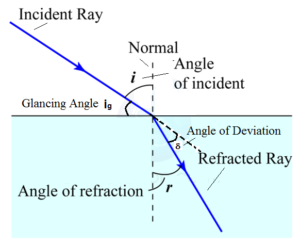
• Optical Medium: The medium capable of transmitting light is called as an optical medium.
• Isotropic medium:
• The homogeneous medium, which has the same properties in all directions is called an isotropic medium.
• Incident ray:
• The light ray, which is falling on reflecting or refracting surface is called the incident ray.
• Point of incidence: The point at which the incident ray cuts the reflecting or refracting surface is called the point of incidence.
• Normal: A perpendicular drawn to the surface at the point of incidence is called the normal.
• Angle of incidence:
• The angle made by the incident ray with the normal at the point of incidence is called the angle of incidence. It is denoted by ‘i’.
• Angle of Refraction:
• The angle made by the refracted ray with the normal at the point of incidence is called the angle of refraction. It is denoted by ‘r’.
• Angle of Deviation:
• The angle between the direction of the incident ray to the direction of the refracted ray is called the angle of deviation. it is denoted by ‘δ’.
• Glancing Angle:
• The angle made by incident ray with a refracting surface or interface is called a glancing angle.

Refractive Index of a Medium:

According to Huygens, the cause of the refraction of light is that the velocity of light is different in different media. The velocity of light is maximum in vacuum and air. The velocity of light in vacuum or air is denoted by letter ‘c’.

The relative refractive index of the second medium with respect to the first medium (₁μ₂)is defined as the ratio of the velocity of light in the first medium (v₁) to the velocity of light in the second medium (v₂). Mathematically,

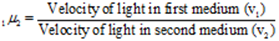
When the first medium is vacuum or air the relative refractive index is known as the absolute refractive index.

Snell’s Law:

The ratio of the sine of the angle of incidence to the sine of the angle of refraction is always constant and is equal to the refractive index of the medium.  This law is known as Snell’s law.

Mathematically,

Principle of Reversibility of Light:

If, after undergoing a number of reflections and refractions, the direction of a ray of light is reversed, the ray traces its original path in the reverse direction. This principle is applicable to prisms and lens also.

Property:

If ₁μ₂ is the  refractive index of the second medium with respect to the first medium  and  ₂μ₁ is  the refractive index of the first medium with respect to the second medium, then

Proof:

To show that ₁μ₂ = μ₂/μ₁

The absolute refractive index of the medium is defined as the ratio of the velocity of light in the vacuum to the velocity of light in the medium.

The absolute refractive index of the first medium = μ₁ = v₁ / c …….. (1)

The absolute refractive index of the second medium = μ₂ = v₂ / c ………. (2)

Dividing equation (2) by equation (1) we have

μ₂/μ₁ =   v₂/v₁    …………………. (3)

The relative refractive index of the second medium with respect to the first medium (₁μ₂)is defined as the ratio of the velocity of light in the first medium (v₁) to the velocity of light in the second medium (v₂). Mathematically,

₁μ₂ = v₂/v₁     …………………. (4)

From equation (3) and (4) we have

₁μ₂ = μ₂/μ₁      (Proved as required)

Numerical Problems on Refractive Index:

Example – 01:

A ray of light in air is incident on a glass surface making an angle of 30° with the surface. the angle of refraction in a glass is 35°16′. Find the angle of deviation of the ray.

Given: Glancing angle = i_g = 30°. Hence angle of incidence = 90° – 30° = 60°

To find: Angle of deviation = δ = ?

Solution:

The angle of deviation = Angle of incidence – Angle of refraction

Angle of deviation = δ = 60° –   35°16′ = 24°44′

Ans:  The angle of deviation of the ray is 24°44′

Example – 02:

Find the refractive index of water. Given velocities of light in air and water as 3 × 10⁸ m/s and 2.25 × 10⁸ m/s respectively.

Given: Velocity of light in air = c = 3 × 10⁸ m/s and velocity of light in water = v = 2.25 × 10⁸ m/s

Fo find: Refractive index of water = μ =?

Solution:

μ = c /ν= 3 × 10⁸ /2.25 × 10⁸ = 1,333

Ans:  The refractive index of water is 1.33

Example – 03:

The refractive index of glass with respect to air is 1.5. Calculate the velocity of light in the glass. Given the velocity of light in the air as 3 × 10⁸ m/s.

Given: Velocity of light in air = c = 3 × 10⁸ m/s and refractive index of glass = μ = 1.5

Fo find: velocity of light in glass = v =?

Solution:

μ = c /v

∴   v = c/μ

∴   v = 3 × 10⁸ /1.5 = 2 × 10⁸ m/s

Ans:  The velocity of light in glass is 2 × 10⁸ m/s

Example – 04:

The refractive index of water w.r.t. air is 4/3. Find the relative refractive index in case when light travels from water into air.

Given: refractive index of water w.r.t. air = _aμ_w = 4/3

Fo find: refractive index of air w.r.t. water = _wμ_a =?

Solution:

_wμ_a ==  1/_aμ_w = 3/4 = 0.75

Ans:  The refractive index of air w.r.t. water is 0.75

Science > Physics > Refraction of Light > Introduction to Refraction of Light