Science > Physics > Gravitation > Keppler’s Laws of Orbital Motion
In this article, we shall study Keppler’s laws of orbital motion and their use to derive Newton’s law of gravitation.
In the second century A.D., Ptolemy proposed a geocentric theory of the universe. According to this theory, the Earth is the centre of the universe and all other planets, sun and other stars revolve around the Earth. Indian astronomer, mathematician and philosopher Aryabhatta in 498 A.D. proposed that not only the Earth revolves around the sun but it rotates around its own axis. Polish astronomer Nicolaus Copernicus (1473 -1543) proposed the heliocentric theory of the universe. According to this theory, the Sun is the centre of the galaxy and all other planets revolve around the Sun. The Danish astronomer Tyco Brahe made the most accurate observations possible before the invention of the telescope. These observations showed discrepancies within Ptolemy’s geocentric theory of the universe.
Johannes Kepler (1571 – 1630) studied data of motion of planets by Danish astronomer Tycho Brahe and put forward his laws of planetary motion. These laws are known as Keppler’s law of orbital motion. He also proposed that the motion of the planet around the sun is not in circular orbit but it is in an elliptical orbit with the Sun at one of the foci of the elliptical orbit. A Netherland’s spectacle maker Hans Lippershey assembled first reflecting telescope. Using this concept Galileo developed his own telescope. Using the telescope he observed skies and substantiated Copernicus’s heliocentric theory of the universe. Further, he observed there are many stars in the universe and the Sun is one of them. He observed that only planets move around the sun. The moon moves around the Earth and Some planets like Jupiter has more than one moon.
There was a curiosity among astronomers about the motion of planets around the sun. For the study of the motion of planets around the sun or satellites around the Earth, we consider gravitational attraction between the sun and the planet or earth and the satellite only. Here we ignore the disturbing effect of the gravitational forces due to other bodies. Another major assumption is that the centre of mass of the sun (earth) and the planet (satellite) system is at their geometrical centre.
Keppler’s Laws:
First Law (Keppler’s Law of Elliptical Orbits – 1609):
Every planet moves around the sun in a closed elliptical orbit with the sun at one of its foci.
The following figure shows the path of the planet around the Earth.
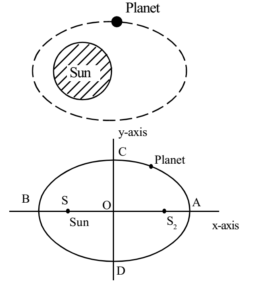
Due to elliptical motion and the Sun at one of the foci, the distance of a planet from the sun changes continuously. The closest point on the orbit of the planet from the sun is B. This closest point on the orbit of the planet to the sun is called perihelion and this minimum distance is called perigee. Thus Perigee = SB = a – ae = a (1 – e). Where ‘a’ is semi-major axis and e is the eccentricity of the ellipse. The farthest point on the orbit of the planet from the sun is A. This farthest point on the orbit of the planet to the sun is called aphelion and this maximum distance is called apogee. Thus Apogee = SA = a + ae = a (1 + e). Where ‘a’ is semi-major axis and e is the eccentricity of the ellipse.
Second Law (Keppler’s Law of Equal Areas – 1609):
The radius vector drawn from the Sun to the planet sweeps out equal areas in equal time. i.e. aerial velocity of the radius vector is constant. Thus the Aerial velocity of the satellite is always constant. i.e. A/t = Constant.
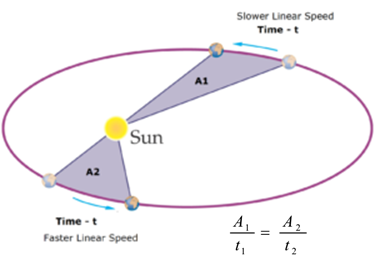
In this case, the planet covers unequal distances in equal time. Thus the planet has variable speed. When the planet is very close to the Sun, the maximum distance is covered in given time. Thus the planet has maximum velocity when it is at perihelion. Hence it has maximum kinetic energy at perihelion. When the planet is very far to the Sun, the minimum distance is covered in given time. Thus the planet has minimum velocity when it is at aphelion. Hence it has minimum kinetic energy at perihelion.
| Point | Perihelion | Aphelion |
| Distance from sun | Minimum | Maximum |
| Distance called | Perigee | Apogee |
| Speed of Planet | Maximum | Minimum |
| The kinetic energy of the planet | Maximum | Minimum |
| The potential energy of the planet | Minimum | Maximum |
Keppler’s Third Law (Keppler’s Law of Period – 1618)
The square of the period of a satellite is directly proportional to the cube of the semimajor axis of its elliptical orbit.
If T is the period of satellite and r is the semimajor axis or the radius of the circular orbit of the satellite.

A similar result is obtained for the elliptical orbit and then the radius r of the circular orbit is replaced by semi-major axis ‘a’.
Note:
Keppler’s laws are empirical laws because they are based on observations and not on theory. Kepler’s laws are applicable whenever an inverse square law is involved. They are applicable to the solar system and artificial satellite systems.
Proof of Keppler’s Law of Equal Areas:

Consider a planet moving in an elliptical orbit from point P1 to point P2, Let in a small interval of time Δt, it traces small area ΔA at the focus S. Let the angle traced by radius vector be Δθ at the Focus S.
The area of the sector is given by

Where ω is the angular velocity of the planet.
Now, the instantaneous angular momentum is given by
L = m r ω2
Thus r ω2 = L/m
Substituting in equation (1) we have

As net torque acting on the planet is zero, the angular momentum is constant. Thus R.H.S. of equation (2) is constant.
Thus dA / dt = constant
Thus the areal velocity of the planet is constant. This proves Keppler’s second law.
Proof of Newton’s Law of Gravitation Using Keppler’s Law:
Let, m = Mass of planet
M = Mass of sun
R = Radius of the orbit of the planet
ωw= Angular velocity of the planet.
F = Centripetal force exerted on planet by the Sun
We know that

By Keppler’s law, we have T2 ∝ r3
T2 = k r3
Substituting in equation(1)

The quantities in the bracket are constant.

Thus force exerted by the sun on the planet is a) directly proportional to the mass ‘m’ of the planet. b) Inversely proportional to the square of the distance ‘R’ between the planet and the sun. Now, the planet will exert equal and opposite force on the sun such that
Now, the planet will exert equal and opposite force on the sun such that

Thus force exerted by the planet on the Sun is a) directly proportional to mass ‘M’ of the Sun and b) inversely proportional to the square of the distance ‘R’ between the planet and the sun.
From (2) and (3) we have

This relation is known as Newton’s law of gravitation.
Previous Topic: Variation in Acceleration Due to Gravity
Next Topic: Numerical Problems on Keppler’s Laws