Numerical Problems on Energy of Particle Performing S.H.M.

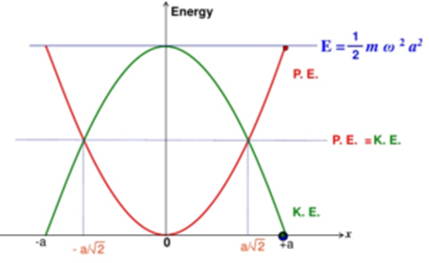
Science > Physics > Oscillations: Simple Harmonic Motion > Numerical Problems on Energy of Particle Performing S.H.M.

In this article, we shall study to solve numerical problems to calculate potential energy, kinetic energy, and total energy of particle performing S.H.M.

Example – 01:

A particle of mass 10 g performs S.H. M. of amplitude 10 cm and period 2π s. Determine its kinetic and potential energies when it is at a distance of 8 cm from its equilibrium position.

Given: Mass = m = 10 g, amplitude = a = 10 cm, Period = T = 2π s, displacement = x = 8 cm

To Find: Kinetic energy =? and Potential energy = ?

Solution:

Angular velocity ω = 2π/T = 2π/2π = 1 rad/s

Kinetic energy = 1/2 mω² (a² – x²) =1/2 x 10 x 1²(10² – 8²)

∴ Kinetic energy = 5 x (36) = 180 erg = 1.8 x 10^-5 J

Potential energy = 1/2 mω²x²

∴ Potential energy = 1/2 x 10 x 1² x 8² = 320 erg = 3.2 x 10^-5 J

Ans: Kinetic energy = 1.8 x 10^-5 J and potential energy = 3.2 x 10^-5 J

Example – 02:

A particle of mass 10 g executes linear S.H.M. of amplitude 5 cm with a period of 2 s. Find its PE and KE, 1/6 s after it has crossed the mean position.

Given: Mass = m = 10 g, amplitude = a = 5 cm, Period = T = 2 s, time elapsed = 1/6 s, particle passes through mean position, α = 0.

To Find: Kinetic energy =? and Potential energy =?

Solution:

Angular velocity ω = 2π/T = 2π/2 = π rad/s

Displacement of a particle performing S.H.M. is given by

x = a sin (ωt + α)

∴ x = 5 sin (π x 1/6 + 0)

∴ x = x = 5 sin (π/6) = 5 x 1/2 = 2.5 cm

Kinetic energy = 1/2 mω² (a² – x²) =1/2 x 10 x π² (5² – 2.5²)

∴ Kinetic energy = 5 x 3.142²(25- 6.25) = 5 x 3.142²(18.75)

∴ Kinetic energy = 925.5 erg = 9.26 x 10^-5 J

Potential energy = 1/2 mω²x²

∴ Potential energy  = 1/2 x 10 x π² x 2.5² = 5 x 3.142² x 2.5²

= 308.5 erg = 3.09 x 10^-5 J

Ans: Kinetic energy = 9.26 x 10^-5 J and potential energy = 3.09 x 10^-5 J

Example – 03:

The total energy of a particle of mass 0.5 kg performing S.H.M. is 25 J. What is its speed when crossing the centre of its path?

Given: Mass = m = 0.5 kg, Total energy T.E. = 25 J

To Find: Maximum speed = v_max =?

Solution:

The speed when crossing mean position is a maximum speed

Total energy = 1/2 mω²a²

∴ 25 = 1/2 x 0.5 x ω²a²

∴ ω²a² = 25 x 2/ 0.5 = 100

∴ ωa = 10 m/s

But ωa = v_max = 10 m/s

Ans: The speed when crossing mean position is 10m/s

Example – 04:

A particle performs a linear S.H.M. of amplitude 10 cm. Find at what distance from the mean position its PE is equal to its KE.

Given: P.E. = K.E.

To Find: Distance = x=?

Solution:

P.E. = K.E.

∴ 1/2 mω²x² = 1/2 mω² (a² – x²)

∴ x² =  a² – x²

∴ 2x² = a²

∴ x = ± a/√2 = ±10/√2 = ±5√2 cm

Ans:  At a distance of 5√2 cm from either side of the mean position K.E. = P.E.

Example – 05:

Find the relation between amplitude and displacement at the instant when the K.E. of a particle performing S.H. M. is three times its P.E.

Given: K.E. = 3 x P.E.

To Find: Distance = x=?

Solution:

K.E. = 3 x P.E.

∴ 1/2 mω² (a² – x²)  = 3 x 1/2 mω²x² 

∴ a² – x² = 3x² 

∴ 4x² = a²

∴ x = ± a/2, where a = amplitude

Ans:  At a distance of a/2 cm from either side of the mean position K.E. = 3 x P.E.

Example – 06:

When is the displacement in S.H.M. one-third of the amplitude, what fraction of total energy is kinetic and what fraction is potential? At what displacement is the energy half kinetic and half potential?

Part – I:

Given: x = a/3

To Find: K.E/T.E. =? and P.E./T.E. =?

Solution:

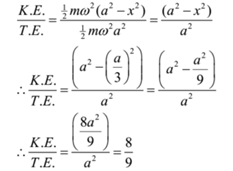
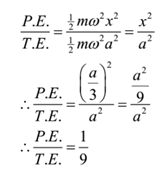
Part – II

Given: P.E. = K.E.

To Find: Distance = x =?

Solution:

P.E. = K.E.

∴ 1/2 mω²x² = 1/2 mω²(a² – x²)

∴ x²  =  a² – x²

∴ 2x² = a²

∴ x = ± a/√2

Ans:  The fraction of K.E = 8/9, fraction of P.E. = 1/9, required displacement = ± a/√2 unit

Example – 07:

An object of mass 0.2 kg executes S.H.M. along the X-axis with a frequency of 25 Hz. At the position x = 0.04 m, the object has a K.E. of 0.5 J and P.E. of 0.4 J. Find the amplitude of its oscillations.

Given: Mass = m = 0.2 kg, frequency = n = 25 Hz, displacement = x = 0.04 m = 4 cm, K.E. = 0.5 J, P.E. = 0.4 J

To Find: Amplitude = a =?

Solution:

Angular speed ω = 2πn = 2 x π x 25 = 50π rad/s

∴   5x² = 4a² – 4x²

∴   9x² = 4a²

∴ 4a² = 9x 4² = 144

∴ a² = 36

∴ a = 6 cm

Ans: The amplitude = 6 cm

Example – 08:

The amplitude of a particle in S.H. M. is 2 cm and the total energy of its oscillation is 3 x 10^-7 J. At what distance from the mean position will the particle be acted upon by a force of 2.25 x 10^-5 N when vibrating?

Given: amplitude = a = 2 cm, Total energy = T.E. = 3 x10^-7 J = 3 x10^-7 x 10⁷ = 3 erg, Force = 2.25 x 10^-5 N = 2.25 x 10^-5 x 10⁵ = 2.25 dyne

To Find: Distance = x =?

Solution:

T.E =1/2 mω²a²

∴ 3 =1/2 mω²(2)²

∴ mω² =3/2 ………… (1)

Now Force F = mf = mω²x

∴ 2.25 = (3/2)x

∴ x = 2.25 x 2 /3 = 1.5 cm

Ans: At a distance of 1.5 cm from the mean position will the particle be acted upon by a force of 2.25 x 10^-5 N

Example – 09:

A body of mass 100 g performs S.H.M. along a path of length 20 cm and with a period of 4 s. Find the restoring force acting upon it at a displacement of 3 cm from the mean position? Find also the total energy of the body.

Given: mass = m = 20 g, Path length = 20 cm, amplitude = a = 20/2 = 10 cm, Period = T = 4s,

To Find: Restoring force = F =? Total energy = T.E. = ?

Solution:

Angular speed ω = 2π/T = 2π/4 = π/2 rad/s

Restoring force F = mf = mω²x

F = 100 x (π/2)² x 3 = 740.4 dyne = 740.4 x 10^-5 N = 7.404 x 10^-3 N

T.E. = 1/2 x 100 x (π/2)²x 10² = 1.234 x 10⁴ erg

T.E. = 1.234 x 10⁴ x 10^-7 J = 1.234 x 10^-3 J

Ans: Restoring force = 7.404 x 10^-3 N; total energy = 1.234 x 10^-3 J

Example – 10:

A particle of mass 200 g performs S.H.M. of amplitude 0.1m and period 3.14 second. Find its K.E. and P.E. when it is at a distance of 0.03 m from the mean position.

Given: mass = m = 200 g, amplitude = a = 0.1 m = 10 cm, period = T = 3.14 s, Distance = x = 0.03 m = 3 cm,

To Find: K.E. =? and P.E. = ?

Solution:

Angular speed ω = 2π/T = 2π/3.14 = 2 rad/s

Kinetic energy = 1/2 mω²(a² – x²) =1/2 x 200 x 2²(10² – 3²)

∴ Kinetic energy = 100 x 4 x (100 -9) = 3.64 x 10⁴ erg

∴ Kinetic energy = 3.64 x 10⁴ x 10^-7 J = 3.64 x 10^-3 J

Potential energy = 1/2 mω²x²

∴ Potential energy = 1/2 x 200 x 2² x 3² = 3.6 x 10³ J

∴ Potential energy = 3.6 x 10³ x 10^-7 = 3.6 x 10^-4 J

Ans: K.E. = 3.64 x 10^-3 J; P.E. = 3.6 x 10^-4 J

Previous Topic: Energy of Particle Performing S.H.M.

Next Topic: Composition of Two S.H.M.s

Science > Physics > Oscillations: Simple Harmonic Motion > Numerical Problems on Energy of Particle Performing S.H.M.