Numerical Problems on Kinetic Theory of Gases

Science > Physics > Kinetic Theory of Gases > Numerical Problems on Kinetic Theory of Gases

In this article, we shall study to find r.ms. speed of gas molecules, density of gas, pressure exerted by the gas using kinetic theory of gases.

Example 01:

Calculate the R.M.S. velocity of Hydrogen molecules at N.T.P. given: Density of Hydrogen at N.T.P. = ρ = 8.957 x 10^-2 kg/m³. Density of mercury = 13600 kg/m³, g = 9.8 m/s².

Given: Density of hydrogen = ρ = 8.957 x 10^-2 kg/m³, condition N.T.P., P = 76 cm of Hg = 0.76 x 13600 x 9. 8 N/m², Density of Mercury = 13600 kg/m³, g = 9.8 m/s².

To Find: r.m.s. speed = C =?

Solution:

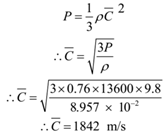
Ans: r.m.s. velocity of hydrogen molecule is 1842 m/s 0r 1.842 km/s

Example 02:

Find the R.M.S. velocity of Nitrogen molecules at N.T.P. given that the density of Nitrogen at this temperature is 1.25 g/litre.

Given: Density = ρ = 1.25 g/litre = 1.25 x 1 = 1.25 kg/m³, condition N.T.P., P = 1.013 x 10⁵ N/m².

To Find: r.m.s. speed = C =?

Solution:

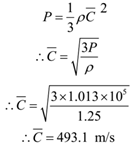
Ans: r.m.s. velocity of nitrogen molecule is 493.1 m/s

Example 03:

Calculate the R.M.S. velocity of Oxygen molecules at a pressure of 1.013 x 10⁵ N/m² (N.T.P.) given the density of Oxygen is 1.44 kg/m³.

Given: Density = ρ = 1.44 kg/m³, P = 1.013 x 10⁵ N/m².

To Find: r.m.s. speed = C =?

Solution:

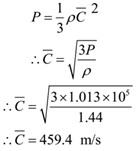
Ans: r.m.s. velocity of oxygen molecule is 459.4 m/s

Example 04:

Calculate the density of He at N.T.P. given that R.M.S. velocity of He molecules at N.T.P. is 1300 m/s.

Given: Condition N.T.P., P = 76 cm of Hg = 0.76 x 13600 x 9.8 = 1.013 x 10⁵ N/m², Density r.m.s. speed = C = 1300 m/s.

To Find: Density = ρ =?

Solution:

Ans: density of He is 0.1798 kg/m³

Example 05:

Determine the pressure of oxygen at 0 °C if the density of oxygen at NTP is 1.44 kg/m³ and r.m.s speed of the molecule at NTP is 456.4 m/s.

Given: Density = ρ = 1.44 kg/m³, condition N.T.P., P = 76 cm of Hg = 0.76 x 13600 x 9.8 = 1.013 x 10⁵ N/m², r.m.s. speed = C = 456.4 m/s

To Find: Pressure of gas = P =?

Solution:

Ans: Pressure of oxygen = 10⁵ N/m²

Example 06:

Two gases are at temperatures of 77 ^oC and 27 ^oC. What is the ratio of the R.M.S. velocities of the molecules of the two gases?

Given: temperature of first gas = T₁ = 77 ^oC = 77 + 273 = 350 K, temperature of second gas = T₂ = 27 ^oC = 27 + 273 = 300 K

To Find: Ratio of r.m.s speeds =?

Solution:

Ans: The ratio of r.m.s. speed is 1.08:1

Example 07:

At what temperature will the R.M.S. speed of the molecules of gas be three times its value at N.T.P.?

Given: Condition = N.T.P., T₁ = 273 K, C₂ = 3C₁

To Find: Temperature = T₂ =?

Solution:

Ans: At a temperature of 2184 °C the r.m.s. speed of the molecules of a gas is three times its value at N.T.P.

Example 08:

At what temperature will the R.M.S. speed of the molecules of gas be four times its value at N.T.P.?

Given: Condition = N.T.P., T₁ = 273 K, C₂ = 4C₁

To Find: Temperature = T₂ =?

Solution:

Ans: At a temperature of 4095 °C the r.m.s. speed of the molecules of a gas is four times its value at N.T.P.

Example 09:

The R.M.S. velocity of Nitrogen molecules at N.T.P. is 497 m/s. Calculate the R.M.S. velocity of Hydrogen molecules at N.T.P. At what temperature will the R.M.S. velocity of Nitrogen molecules be 994 m/s?

Part – I:

Given: For nitrogen: Condition = N.T.P., T_N = 273 K, C_N = 497 m/s, P_N = 1.013 x 10⁵ N/m², for oxygen: Condition = N.T.P., T_N = 273 K, P_H = 1.013 x 10⁵ N/m².

To Find: r.m.s. speed of hydrogen = C_H =?

Solution:

Part – II:

Given: Condition = N.T.P., T₁ = 273 K, C₁ = 497 m/s, C₂= 994 m/s

To Find: Temperature = T₂ =?

Solution:

Ans: r.m.s. speed of hydrogen molecules at NTP1860 m/s, at a temperature of 819oC the speed of nitrogen molecules at NTP 994 m/s,

Example 10:

Calculate the R.M.S. velocity of Oxygen molecules at 27 °C. The density of Oxygen at N.T.P. 1.44 kg/m³.

Given: For nitrogen: Condition = N.T.P. T₁ = 273 K, P = 76 cm of Hg = 0.76 x 13600 x 9.8 = 1.013 x 10⁵ N/m², density of oxygen = ρ = 1.44 kg/m³, Temperature = T₂ = 27 ^oC= 27 = 273 = 300 K

To Find: r.m.s. speed = C₂ =?

Solution:

Now C₁ = 459.4 m/s, T₁ = 273 K, = T₂ = 27 ^oC= 27 = 273 = 300 K, C₂ = ?

Ans: The R.M.S. velocity of Oxygen molecules at 27 °C is 481.6 m/s

Example 11:

Compute the R.M.S. velocity of Oxygen molecules at 127 °C. Density of Oxygen at N.T.P. = 1.44 kg/m³.

Given: For nitrogen: Condition = N.T.P. T₁ = 273 K, P = 76 cm of Hg = 0.76 x 13600 x 9.8 = 1.013 x 10⁵ N/m², density of oxygen = r = 1.44 kg/m³, Temperature = T₂ = 127 ^oC= 127 = 273 = 400 K

To Find: r.m.s. speed = C₂ =?

Solution:

Now C₁ = 459.4 m/s, T₁ = 273 K, = T₂ = 127 ^oC= 127 = 273 = 400 K, C₂ =?

Ans: The R.M.S. velocity of Oxygen molecules at 127 °C is 556.1 m/s.

Example 12:

Calculate the R.M.S. velocity of Oxygen molecules at 225 °C. The density of oxygen at NTP is 1.42 kg/m⁵ and 1 atmosphere = 1.013 x 10⁵ N/m².

Given: For nitrogen: Condition = N.T.P. T₁ = 273 K, P = 76 cm of Hg = 0.76 x 13600 x 9.8 = 1.013 x 10⁵ N/m², density of oxygen = ρ = 1.44 kg/m³, Temperature = T₂ = 225 ^oC= 225 + 273 = 498 K

To Find: r.m.s. speed = C₂ =?

Solution:

Now C₁ = 459.4 m/s, T₁ = 273 K, = T₂ = 127 ^oC= 127 = 273 = 400 K, C₂ = ?

Ans: The R.M.S. velocity of Oxygen molecules at 127 °C is 624.8 m/s

Example 13: 

The density of a gas is 0.178 kg/m³ at N.T.P. Find the R.M.S. velocity of gas molecules. By what factor will the velocity of molecules increase at 200 °C?

Given: For nitrogen: Condition = N.T.P. T₁ = 273 K, P = 76 cm of Hg = 0.76 x 13600 x 9.8 = 1.013 x 10⁵ N/m², density of oxygen = ρ = 0.178 kg/m³, Temperature = T₂ = 200 ^oC= 200 + 273 = 473 K

To Find: r.m.s. speed = C₂/ C₁=?

Solution:

Now T₁ = 273 K, = T₂ = 200 ^oC= 200 + 273 = 473 K

Ans: The r.m.s. velocity of the gas molecule at NTP is 1.306 km/s. The r.m.s. velocity will increase by a factor of 1.316 at 200 °C.

Example 14: 

R M.S. velocity of oxygen molecules at 27 °C is 500 m/s. Calculate the R.M.S. and mean square velocities of oxygen molecules at 127 °C.

Given: C1 = 500 m/s at temperature T₁ = 27 ^oC = 27 + 273 = 300 K, Required speed at temperature = T₂ = 127 ^oC = 127 + 273 = 400 K,

To Find: C₂ =? and (C₂)²

Solution:

(C₂)² = (577.4)² = 3.33 x 10⁵ m²/s²

Ans: r.m.s. velocity is 577.4 m/s, and mean square velocity is 3.33 x 10⁵ m²/s²

Example 15:

Taking the R.M.S. velocity of Hydrogen molecules at N.T.P. as 1.84 km/s, calculate the R.M.S. velocity of Oxygen molecules at N.T.P. Molecular weights of Oxygen and Hydrogen are 32 and 2 respectively.

Given: r.m.s. velocity of hydrogen = C_H = 1.84 km/s, molecular mass M_O = 32, M_H = 2, temperature T_H = T_O = 273 K, pressure P_H = P_O = 1.013 x 10⁵ N/m².

To Find: r.m.s. velocity of oxygen molecule = C_O =?

Solution:

Ans: The R.M.S. velocity of Oxygen molecules at N.T.P. is 0.46 km/s

Example 16:

R.M.S. speed of Oxygen molecules is 493 m/s at a certain temperature. Calculate the R.M.S. speed of helium molecules at the same temperature. Molecular weights of Oxygen and Helium are 32 and 4 respectively.

Solution:

Given: r.m.s. velocity of oxygen = C_O = 493 m/s, molecular mass M_O = 32, M_He = 4,
temperature T_He = T_O, Pressure P_He = P_O.

To Find: r.m.s. velocity of helium molecule = C_He=?

Ans: The r.m.s. speed of helium molecule is 1394.2 m/s

Example 17:

R.M.S. speed of Oxygen molecules at N.T.P. is 459.3 m/s. Find the R.M.S. speed of Nitrogen molecules at 340 K. Molecular weights of Oxygen and Nitrogen are respectively 32 and 28.

Given: r.m.s. speed of oxygen = C_O1 = 459.3 m/s, T_O1 = 273 K, T_O2 = 340 K  = T_N , M_O = 32, M_N = 28

To Find: C_N =?

Solution:

Ans: r.m.s speed of nitrogen at 340 K is 548 m/s

Previous Topic: Expression for Pressure Exerted by a Gas

Next Topic: Specific Heats of Gases

Science > Physics > Kinetic Theory of Gases > Numerical Problems on Kinetic Theory of Gases