Science > Physics > Kinetic Theory of Gases > Introduction to Kinetic Theory of Gases
In this article, we shall study a very important concept called kinetic theory of gases, using which we can explain behaviour of the gases.
Ideal Gas:
A gas which obeys gas laws at all temperatures and pressures is called an ideal gas or Perfect gas e.g. an ideal gas does not liquefy even at low temperature but continues to obey Charle’s law and finally occupies no volume at –273 oC or 0 K.
Ideal gas consists of molecules in a continuous state of motion with neither attraction nor repulsion between them. Molecules of ideal gas collide with each other without any net loss of kinetic energy.
For an ideal gas, PV = nRT.
This relation is known as the ideal gas equation. Where, P = Pressure of the gas, V = Volume of the gas, n = number of moles of the gas, R = Universal gas constant, T = Absolute temperature of the gas.
In reality, there exists some negligible force of attraction and repulsion between the molecules of the gas. Besides, there is some loss of kinetic energy in the collision of the molecules of the gas. Hence ideal gas is an imaginary or hypothetical concept. Gas is said to non-ideal or real gas if it obeys gas laws only at low pressures and high temperatures.
Avogadro’s Hypothesis:
Equal volumes of all gases under the same conditions of temperature & pressure contain an equal number of molecules.
Explanation:
Let the pressure of the two gases be the same (P). By Avogadro’s law under such conditions of equal pressure, equal volume & equal temperature, the number of molecules of gas A in the container should be equal to the number of molecules of gas B in the container.
Importance of Avogadro’s Hypothesis:
- It differentiates between atoms and molecules of gasses.
- It modified Dalton’s atomic theory.
- It explains Gay-Lussac’s law of combining volume.
- It helps in the determination of the atomic mass of elements.
- It established that the number of molecules per unit volume is the same for all gases at a fixed temperature and pressure.
- It established that at N.T.P.one gram mole of any gas occupies 22.4 dm3 by volume. one mole of gas contains 6.023 X 1023 molecules of gas.
- It gives the relation between vapour density & molecular weight.
Molecular weight = 2 × vapour density.
Kinetic Theory of Gases:
Evidences of the Molecules of a Gas are Always in Constant Motion:
- Diffusion of gases.
- Indefinite expansion of gases.
- Gases exert pressure on the walls of the container.
- Brownian like motion in gases.
Assumptions of Kinetic Theory of Gases:
- A gas consists of a large number of extremely small molecules which are exactly identical in all respects.
- The molecules are rigid and perfectly elastic spheres of very small diameters.
- The intermolecular forces between gas molecules are negligible.
- The molecules are in a state of random motion i.e. they move with all possible velocities in all possible directions.
- During their random motion the molecules collide with each other and with the walls of the container and these collisions are supposed to be perfectly elastic, (i.e. there is no loss of kinetic energy during these collisions).
- Between successive collisions, molecules move with uniform velocity in straight paths and these paths are called free paths.
- All free paths are not equal. Average of free paths is called mean free path.
- The actual volume of the molecules is negligible compared to the total volume of the gas. Therefore, molecules can be treated as geometrical points.
- The number of molecules per unit volume of a gas remains constant.
- At constant temperature, the average kinetic energy of the gas molecules remains constant. The average kinetic energy of the molecules of a gas depends only on the absolute temperature of the gas.
- The time of impact i.e. the time interval during which collision occurs is very small compared to the time interval between successive collisions.
Terminology of Kinetic Theory of Gases:
Mean Free Path of Gas Molecule:
The molecules of a gas are always moving in random motion i.e. in all possible directions with all possible velocities. This is also called as molecular chaos. Therefore they constantly collide with one another and with the walls of the container.
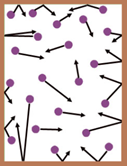
Between two successive collisions, a molecule travels in a straight line. The distance covered by a molecule between two successive collisions is called the free path.
All the free paths are not equal. Therefore their average value is considered. The average distance covered by a molecule between successive collisions is called its mean free path. It is denoted by ‘λ’. Its S.I. unit is m but the practical unit is angstrom.
If λ1, λ2,l3, ….., λN are the free paths, then mean free path is given by
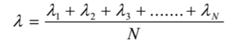
Where N is a number of collisions.
Mean or Average Velocity:
The mean velocity of a molecule of a gas is defined as the arithmetic mean of the velocities of the molecules of the gas at a given temperature.
Let C1, C2, C3, …. , CN be the velocities of N molecules of a gas, then the mean velocity of molecules of a gas is given by
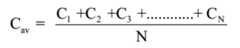
As the molecules of gases are in random motion, i.e. they can move in any direction with any possible velocity, by the probability theory the mean velocity of gas molecules should be zero. Its S.I. unit is m/s.
Mean Square Velocity of Gas Molecules:
The mean square velocity of a molecule of a gas is defined as the arithmetic mean of squares of the velocities of the molecules of the gas at a given temperature.
LetC1, C2, C3, …. , CN be the velocities of N molecules of a gas, then the mean velocity of molecules of a gas is given by

Its S.I. unit is m²/s².
Root Mean Square Velocity of Gas Molecules:
The square root of the mean of the squares of the velocities of the molecules of a gas is called root mean square (r.m.s.) velocity of the molecules of a gas.
Let C1, C2, C3, …. , CN be the velocities of N molecules of a gas, then the r.m.s. velocity of molecules of a gas is given by

It is clear that r.m.s. Velocity cannot be zero.
Numerical Problems:
Example 01:
In the following table, ni represents the number of molecules of a gas and Ci represents their speed in m/s Calculate the average and R.M.S. speeds of the molecules.
| ni | 2 | 4 | 8 | 6 | 3 |
| Ci | 1 | 2 | 3 | 4 | 5 |

Ans: Average speed of molecule is 3.173 m/s and r.m.s. speed is 3.369 m/s
Example 02:
Find the average velocity, mean square velocity and root mean square velocity of six molecules having velocities 4, 5, 8, -6, -4, and 10 m/s respectively.

Ans: average speed = 2.83 m/s, mean square speed = 42.83 m2/s2; rms speed = 6.544 m/s
Example 03:
The velocities of seven molecules are 1, 2, 3, 4, 5, 6, 7 km/s respectively. Find the mean square velocity of the molecule.

Ans : Mean square velocity = 20 km2/s2
Example 04:
Find the r.m.s. velocity of three molecules having velocities 10, 20, 30 km/s.

Ans: r.m.s. speed = 21.60 km/s
Next Topic: Expression for Pressure Exerted by a Gas
One reply on “Kinetic Theory of Gases”
very nice note