Science > Physics > Radiation > Kirchhoff’s law of Radiation
In this article, we shall study Kirchhoff’s law of radiation and its theoretical and experimental proof.
Statement:
The ratio of the emissive power to the coefficient of absorption is constant for all substances at a given temperature and is equal to the emissive power of a perfectly black body at that temperature. OR At any given temperature, the emissivity (or coefficient of emission) of a body is equal to the coefficient of absorption
Explanation:
If ‘E’ is the emissive power of a substance and ‘a’ is its coefficient of absorption then by Kirchhoff’s law of radiation
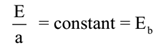
i.e a = e
Theoretical Proof of Kirchhoff’s Law of Radiation:
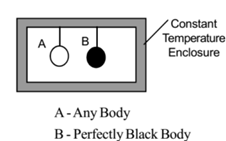
Let us consider two bodies A and B suspended in a constant temperature enclosure. B is a perfectly black body. After some time both A and B will attain the same temperature as that of the enclosure. By Prevost heat exchange theory in this state also every body will emit and absorb thermal radiations.
Let E be the emissive power of A and ‘a’ be its coefficient of absorption. Let Eb be the emissive power of B. Let Q be the radiant heat incident per unit time per unit area of each body.
Heat absorbed per unit time per unit area of A = a Q
Heat emitted per unit time per unit area of A = E.
As the temperature remains constant so the heat emitted will be equal to the heat absorbed
∴ E = a Q …………(1)
Perfectly black body B will absorb all the radiant heat incident on it.
Heat absorbed per unit time per unit area of B = Q.
The heat emitted per unit time per unit area of B = Eb
As the temperature of B remains constant so in case of B also heat emitted is equal to the heat absorbed.
Eb = Q …………..(2)
Dividing equation (1) by (2) we get,

Thus, the coefficient of emission is equal to the coefficient of absorption. This proves Kirchhoff’s law of radiation theoretically.
Experimental Proof of Kirchhoff’s Law or Ritchie’s Experiment:
Apparatus:

The apparatus consists of a U – tube manometer containing some coloured liquid. The two arms of the manometer are connected to two identical cylinders P and Q, having the same axis (co-axially arranged). The same face (either left or right) of each cylinder is coated with lamp black while the other face is kept polished. A third cylinder R can be placed between P and Q co-axially. One face of the cylinder R is coated with lamp black while the other face is kept polished. The cylinder R can be rotated about a vertical axis.
Working:
The cylinder R is kept as shown in the figure such that all black surface point in the same direction. Hot water is poured into the cylinder R due to which its temperature will increase. No change will be observed in the liquid levels in the manometer. This shows that the quantity of heat absorbed by both P and Q from R is the same. Therefore pressure exerted by the air in P and Q on the liquid is the same on both sides.
Let E and Eb be the emissive powers of the polished and black surfaces and ‘a’ be the coefficient of absorption of the polished face. Let A be the area of the cross-section of each cylinder.
The amount of heat radiated per unit time by the black face of R = A Eb.
A part of this heat is the incident on the polished face of P.
Heat incident per unit time on the polished face of P = k A Eb,
The constant k depends upon the distance between P and R.
Heat absorbed per unit time by P per second = a k A Eb.
Heat radiated per unit time by the polished face of R = A E
Heat incident per unit time on the black face of Q = k A E
Heat absorbed per unit time by the black face of Q = k A E.
The level of coloured liquid in both the arms of the apparatus is the same.
Hence both P and Q absorbed same quantity of heat per unit time.
∴ a k A Eb = k A E
∴ a Eb = E
∴ a = E / Eb = e
Thus, the coefficient of absorption = coefficient of emission.
This is Kirchhoff’s law of radiation. Thus the Kirchoff’s Law is experimentally verified.
Numerical Problems:
Example – 01:
512 J of radiant heat are incident on a body which absorbs 224 J. What is its coefficient of emission?
Given: Radiant heat incident = Q = 512 J, radiant heat absorbed = Qa = 224 J
To Find: Coefficient of emission = e =?
Solution:
Coefficient of absorption = a = Qa/Q = 224/512 = 0.4375
By Kirchhoff’s law of radiation
Coefficient of emission (e) = Coefficient of absorption (a)
∴ e = 0.4375
Ans: Coefficient of emission = 0.4375
Example – 02:
A body of surface area 15 × 10-3 m² emits 1260 J in 40 s at a certain temperature. What is the emissive power of the surface at that temperature?
Given: Surface area = A = 15 × 10-3 m², radiant heat emitted = Q = 1260 J, time taken = t = 40 s.
To Find: Emissive power = E =?
Solution:
E = Q/At = 1260 /(15 × 10-3× 40) = 2100 J/m²s
Ans: Emissive power of surface = 2100 J/m²s
Example – 03:
The emissive power of a sphere of area 0.02 m² is 2100 J/m²s. What is the amount of heat radiated by the spherical surface in 20 seconds?
Given: Surface area = A = 0.02 m², Emissive power = 2100 J/m²s, time taken = t = 20 s.
To Find: Heat radiated = Q =?
Solution:
E = Q/At
∴ Q = E A t
∴ Q = 2100 × 0.02 × 20
Ans: Heat radiated = 840 J
Example – 04:
The energy of 6000 J is radiated in 5 minutes by a body of surface area 100 cm2. Find the emissive power of the body.
Given: Radiant heat emitted = Q = 6000 J, Time taken = 5 min = 5 × 60 = 300 s, Surface area = 100 cm² = 100 × 10-4 m²
To Find: Emissive power = E =?
Solution:
E = Q/At = 6000 / (100 × 10-4× 300)
∴ Q = 2000 J/m²s
Ans: Emissive Power = 2000 J/m²s
Previous Topic: Introduction to Radiation
Next Topic: Concept of Black Body