Law of Conservation of Momentum

Science > Physics > Force > Law of Conservation of Momentum

In this article, we shall study the law of conservation of momentum and its proof.

Statement:

When the resultant external force acting on a system is zero, the total linear momentum of the system is constant. OR When no external force acts on a system of bodies and there is collision among them then the total linear momentum before the collision equals to the total momentum after the collision.

Explanation :

Let us consider two bodies having masses m₁ and m₂ moving towards each other along the same straight line with velocities u₁ and u₂ respectively. Let v₁ and v₂ be their velocities after the collision.

By the law of conservation of momentum,The total momentum of the system before collision   = The total momentum of the system after collision

m₁u₁+ m₂u₂ = m₁v₁+ m₂v₂.

This law is universal because It is not only true for the collision of astronomical bodies but also for collision of subatomic particles.

Proof:

Let us consider two bodies having masses m₁ and m₂ moving towards each other along the same straight line with velocities u₁ and u₂ respectively.

The total momentum of the system before collision   = m₁u₁ – m₂u₂    …………….(1)

When two bodies collide body of mass m₁ exerts pressure F on the body of mass m2. This is action. By Newton’s third law of motion body of mass m2 exerts force   – F on the body of mass m₁. This is a reaction. Thus resultant force acting on the system is zero.

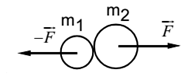
Let the bodies of mass m₁ and m₂ move with velocities  v₁ and v₂ respectively as shown in the diagram.

The total momentum of the system after  collision = – m₁v₂ + m₂v₂   ……….. (2)

From equations (3) and (4) Thus, the total momentum of the system before collision   = The total momentum of the system after the collision. Thus the law of conservation of momentum is proved.

Numerical Problems:

Example – 01:

A ball of mass 100 g moving at a speed of 12 m/s strikes another ball of mass 200 g at rest. After the collision both the balls stick to each other and move with a common velocity. Find the common velocity.

Given : mass of first ball = m₁ = 100 g = 0.1 kg , initial velocity of first ball = u₁= 12 m/s, mass of the second ball = m₂ = 200 g = 0.2 kg , initial velocity of second ball = u₂ = 0 m/s,

To Find: common velocity = v = ?

Solution:

Let v m/s be their common velocity after collision

Final velocitie v₁ = v₂ = v ms-1.

By Law of Conservation of momentum

m₁u₁+ m₂u₂ = m₁v₁+ m₂v₂

∴  (0.1)(12) + (0.2)(0) = (0.1)(v) + (0.2)(v)

∴  1.2 + 0 = 0.3 v

∴  v = 1.2/0.3 = 4 m/s

Ans: Their common velocity is 4 m/s

Example – 02:

A gun fires a bullet of mass 50 g with a velocity of 30 m/s because of which the gun recoils with a velocity 1 m/s. Find the mass of the gun.

Given : mass of bullet = m₁= 50 g = 0.050 kg , velocity of bullet = v₁ = 30 m/s, recoil velocity of gun = v₂ = 1 m/s.

To Find:  mass of gun = m₂ = ?

Solution:

By law of conservation of momentum

Mass of gun x Recoil velocity of gun = Mass of bullet x Velocity of bullet

m₁v₁ = m₂v₂

∴  0.050 x 30 = m₂ x 1

∴  m₂ = 1.5 kg

Ans: The mass of the gun is 1.5 kg.

Example – 03:

A railway engine of mass 2 tons moving at a speed of 72 km/hr, collides with a wagon at rest. After the collision, both have a common velocity of 36 km/hr. Find the mass of the wagon.

Given : mass of engine = m₁ = 2 T = 2000 kg, initial velocity of engine = v₁ = 72 km/hr = 72 x 5/18 = 20 m/s, Mass of wagon = m₂ = Mass of wgon

To Find: Mass of wagon = m₂ = ?

Solution:

Let ‘v m/s be their common velocity after collision

v₁ = v₂ = v  = 36 km/hr = 36 x 5/18 = 10 m/s

By Law of Conservation of momentum

m₁u₁+ m₂u₂ = m₁v₁+ m₂v₂

∴  (2000)(20) + (m2)(0) = (2000)(10) + (m₂)(10)

∴  40000 + 0  = 20000 + 10(m₂)

∴  40000 – 20000 = 10(m₂)

∴  20000 = 10(m₂)

∴  m₂ = 20000/10 = 2000 kg

Ans: The mass of the wagon 2000 kg.

Example – 04:

A bullet of mass 50 g is fired from a gun. If the bullet acquires a velocity of 100 m/s in 0.1secondsd. What is the recoil force on the gun?

Given : mass of bullet = m = 50 g = 0.05 kg, initial velocity of bullet = u = 0, final velocity of bullet = v = 100 m/s, time taken = t = o.1 s

To Find:  recoil force = F = ?,

Solution:

a = (v – u)/t = (100 – 0)/0.1 = 100/0.1 = 1000 m/ s²

Force on bullet = m.a = 0.050 X 1000 = 50 N

By Newton’s third law of motion, the recoiling force on the gun is 50N.

Ans: Recoil force on the gun is 50 N

Previous Topic: Simple Numerical Problems on Force

Next Topic: Elastic and Inelastic Collision

Science > Physics > Force > Law of Conservation of Momentum